机器学习笔记

此份笔记是本人学习过程中自己总结记录的，其内容受到课堂教学内容、采用教材、个人认知水平的影响。虽然笔者力图保证内容准确以及易于理解（起码自己能看懂），但难免存在谬误或者渲染问题。非常欢迎您通过邮件等方式联系我修改，让我们一起让这份笔记变得更好！

第一讲 线性回归

1、基本概念

回归（Regression） 是基于几个给定的特征值，预测与这几个特征相关的未知值。

从数学的角度，回归的目标是学习出一个函数 $f(\cdot)$ ，可以很好地拟合输入$\boldsymbol{x}$和输出$y$之间的关系。

线性回归指限定函数族为线性函数时的回归：

$$f(\boldsymbol{x})=w_0+w_1x_1+w_2x_2+\dots+w_mx_m$$

线性回归的目标就是找到一组合适的参数$\{w_k\}_{k=1}^m$使得训练集中的数据点通过函数$f$得到的预测值$\hat{y}$，与对应的真实值$y$尽可能的接近。

2、单个特征的线性回归

此时输入是一维的，预测函数可以直接写成：

$$f(x)=w_0+w_1x$$

在几何上，这就是一条直线。这条直线在数据平面上与数据点的分布越贴合，说明拟合效果越好。

假设有$n$个数据点，每个数据点记为$(x^{(i)}, y^{(i)})$。我们可以定义损失函数：

$$L(w_0, w_1)=\frac 1 n\sum_{i=1}^n(f(x^{(i)})-y^{(i)})^2$$

来度量与真实数据的“拟合程度”。则目标就是确定能最小化这个函数值的参数。

---

考虑$w_0=0$时的情况。此时损失函数变为：

$$L(w_1)=\frac 1 n\sum_{i=1}^n(w_1x^{(i)}-y^{(i)})^2=w_1^2\frac{\sum_{i=1}^n (x^{(i)})^2}{n}-2w_1\frac{\sum_{i=1}^n (x^{(i)}y^{(i)})}{n}+\frac{\sum_{i=1}^n (y^{(i)})^2}{n}$$

如果将输入写成向量的形式，可以简记为：$L(w_1)=w_1^2\overline{\boldsymbol{x}^2}-2w_1\overline{\boldsymbol{xy}}+\overline{\boldsymbol{y}^2}$，其中上划线是平均值的意思

这个函数是一个凸函数（$w_0\neq 0$时，这个函数也是一个凸函数），令其偏导为 0：

$$\frac{\partial{L}}{\partial{w_0}}=0, \frac{\partial{L}}{\partial{w_1}}=0$$

即可求出最优的参数：

$$w_0=\frac{\overline{\boldsymbol{xy}}\cdot\overline{\boldsymbol{x}}-\overline{\boldsymbol{x}^2}\overline{\boldsymbol{y}}}{\overline{\boldsymbol{x}}^2-\overline{\boldsymbol{x}^2}}, w_1=\frac{\overline{\boldsymbol{x}}\cdot\overline{\boldsymbol{y}}-\overline{\boldsymbol{xy}}}{\overline{\boldsymbol{x}}^2-\overline{\boldsymbol{x}^2}}$$

3、多特征线性回归

输入为$\boldsymbol{x}$，预测函数：

$$f(\boldsymbol{x})=w_0+w_1x_1+w_2x_2+\dots+w_mx_m$$

如果将输入写成：$\boldsymbol{x}=[1, x_1, x_2, \dots,x_m]$，则预测函数可以写为向量形式：

$$f(\boldsymbol{x})=\boldsymbol{xw}$$

其中$\boldsymbol{w}=[w_0, w_1, \dots, w_m]^T$

---

损失函数可以写为：

$$L(\boldsymbol{w})=\frac 1 n \sum_{i=1}^n (\boldsymbol{x}^{(i)}\boldsymbol{w}-y^{(i)})^2$$

如果将$n$个输入点写成矩阵的形式：$\boldsymbol{X}=[\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \dots, \boldsymbol{x}^{(n)}]^T$，则损失函数可以写为：

$$L(\boldsymbol{w})=\frac 1 n \Vert \boldsymbol{Xw}-\boldsymbol{y}\Vert^2$$

这也是一个凸函数，令其导数为 0：

$$\frac{\partial L(\boldsymbol{w})}{\partial \boldsymbol{w}}=\frac 2 n \boldsymbol{X}^T(\boldsymbol{Xw}-\boldsymbol{y})=\boldsymbol{0}$$

所以可解得：

$$\boldsymbol{w}^*=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}$$

特征数为 1 时，这个式子就退化到单变量线性回归中推导出来的式子。

---

偏导数表达式的推导过程：

$$\frac{\partial{\Vert\boldsymbol{Xw}-\boldsymbol{y}\Vert^2}}{\partial{\boldsymbol{w}}}=\frac{\partial{(\boldsymbol{Xw}-\boldsymbol{y})^T}}{\partial{\boldsymbol{w}}}\frac{\partial \Vert\boldsymbol{Xw}-\boldsymbol{y}\Vert^2}{\partial{(\boldsymbol{\boldsymbol{Xw}-\boldsymbol{y}})}}=\boldsymbol{X}^T\cdot 2(\boldsymbol{Xw}-\boldsymbol{y})$$

---

偏导为 0，也即 $\boldsymbol{X}^T(\boldsymbol{Xw}^{*}-\boldsymbol{y})=\boldsymbol{0}$，则几何上有 $\boldsymbol{y}-\boldsymbol{Xw}^{*}\perp \text{span}\{\boldsymbol{x}^{(1)},\boldsymbol{x}^{(2)}, \dots, \boldsymbol{x}^{(n)}\}$

也即最优的 $\boldsymbol{w}^{*}$ 会使得 $\boldsymbol{Xw}^{*}$ 恰好是$\boldsymbol{y}$在$\boldsymbol{x}^{(1)},\boldsymbol{x}^{(2)}, \dots, \boldsymbol{x}^{(n)}$张成的空间中的投影

4、数值优化

解析解并不总是存在或者方便计算。例如上面的多特征线性规划，其中要对一个矩阵求逆。当这个矩阵较大时，是非常困难的。所以我们通常利用一些数值方法，简化计算。

如梯度下降法：

$$\boldsymbol{w}^{(t+1)}=\boldsymbol{w}^{(t)}-r\cdot \frac{\partial L(\boldsymbol{w})}{\partial \boldsymbol{w}}\Bigg|_{\boldsymbol{w}=\boldsymbol{w}^{(t)}}$$

其中$r$为学习率。利用这种方法，只需要计算偏导数值，比直接计算解析解的值要容易许多。

用合适的学习率时，可以逐步收敛到最优解。

---

一种改进是随机梯度下降法（Stochastic Gradient Descent, SGD）

梯度下降法中，每次更新，都用到了所有的数据点，这对于训练集较大的情况并不友好。为了减少复杂度，我们可以只利用一部分数据点$\mathcal{B_t}$来计算梯度：

$$\frac{\partial L(\boldsymbol{w})}{\partial \boldsymbol{w}}\approx\frac{1}{|\mathcal{B_t}|}\sum_{i\in \mathcal{B_t}} \frac{\partial (\boldsymbol{x}^{(i)}\boldsymbol{w}-y^{(i)})^2}{\partial \boldsymbol{w}}$$

可以证明，这是真实全数据点梯度的无偏估计，也即：

$$\mathbb{E}_{B_t}\left[\frac1{|\mathcal{B}_t|}\sum_{i\in\mathcal{B}_t}\frac{\partial(\boldsymbol{x}^{(i)}\boldsymbol{w}-y^{(i)})^2}{\partial\boldsymbol{w}}\right]=\frac{\partial L(\boldsymbol{w})}{\partial\boldsymbol{w}}$$

第二讲 线性分类器

1、二分类问题

在分类问题时，最后的标签是离散的。特别地，在二分类中，用 0 和 1 两种结果值表示两个类$y\in\{0, 1\}$

我们引入 sigmoid 函数（逻辑函数），来将值域变换到$[0,1]$之间：

$$\sigma(z)=\frac{1}{1+e^{-z}}$$

我们将$f(\boldsymbol{x})=\sigma(\boldsymbol{xw})$这样的回归称之为逻辑回归。

---

要实现分类，我们希望真实的标签值为 1 时，预测值尽量接近 1；真实标签为 0 时，预测值尽量接近 0。

采用$f(\boldsymbol{x})=\sigma(\boldsymbol{xw})$作为预测函数，可以定义损失函数：

$$L(\boldsymbol w)= \begin{cases} -\log(\sigma(\boldsymbol{xw})), &y=1\\ -\log(1-\sigma(\boldsymbol{xw})), &y=0\\ \end{cases}$$

也可以写成等价形式：

$$L(\boldsymbol w)=-y\log(\sigma(\boldsymbol{xw})) -(1-y)\log(1-\sigma(\boldsymbol{xw}))$$

这种形式的损失函数，我们称之为交叉熵

交叉熵函数是凸的，比非凸的平方误差更容易优化。

---

交叉熵的梯度：

$$\frac{\partial L(\boldsymbol{w})}{\partial \boldsymbol{w}}=\frac 1 N \sum_{i=1}^N[\sigma(\boldsymbol{x}^{(i)}\boldsymbol{w})-y^{(i)}]\boldsymbol{x}^{ {(i)}T}$$

由于其是凸的，令梯度为 0 即可得到最优的$\boldsymbol{w}^*$，但是这里其解析解是不存在的，可以用梯度下降法等数值解法求得。

---

最终，利用最优的$\boldsymbol{w}^*$，我们这样进行分类：计算$f(\boldsymbol{x})=\sigma(\boldsymbol{xw})$，如果其不小于 0.5，预测值为 1；如果小于 0.5，预测值为 0。

一个完全等价的方法是，将决策边界调整为 0，则此时$\boldsymbol{xw}=0$。在空间中，这就是一个垂直于$\boldsymbol{w}$的超平面。

一般地，对于一个固定的向量$\boldsymbol{w}\in \R^k$，点集$\boldsymbol{x}\in\{\boldsymbol{x}|\boldsymbol{xw}=0\}$构成了一个$K-1$维超平面。

所以，本质上逻辑回归+交叉熵还是在空间中画一个超平面将数据点分成两边，无法表达非线性的决策边界。这也是为什么逻辑回归称之为线性分类器，这里的线性指决策平面是线性的。

2、多分类问题

对于多分类问题，一种方法是将其视为若干个二分类问题；另一种方法是直接将其分为某一类。

---

对于第一种方法，假设共有$K$类，则对应有$K$个预测函数$f_i(\boldsymbol{x})$。对于某个样本$\boldsymbol{x}_0$，其被分到第$k$类：

$$k=\arg\max_i f_i(\boldsymbol{x})$$

---

对于第二种方法，引入了 softmax 函数：

$$\text{softmax}_i(\boldsymbol{z})=\frac{e^{z_i}}{\sum_{k=1}^K e^{z_k}}$$

一个显然的性质是$\sum_{i=1}^K \text{softmax}_i(\boldsymbol{z})=1$

于是样本$\boldsymbol{x}$被分到第$i$类的概率可以写为：

$$f_i(\boldsymbol{x})=\text{softmax}_i(\boldsymbol{xW})=\frac{e^{\boldsymbol{xw}_i}}{\sum_{k=1}^Ke^{\boldsymbol{xw}_k}}$$

这里$\boldsymbol{W}=[\boldsymbol{w}_1, \boldsymbol{w}_2, \dots, \boldsymbol{w}_K]$。如果样本$\boldsymbol{x}$的真实标签是第$i$类，就需要让$f_i(\boldsymbol{x})$尽可能的大。

两个类的 softmax 分类，等价于上一节的逻辑回归，只是参数$\boldsymbol{w}=\boldsymbol{w}_1-\boldsymbol{w}_2$

---

将真实标签$y$写成独热编码$\boldsymbol{y}$。目标是最大化属于样本对应类别的概率，则损失概率可以写为：

$$L(\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_K)=-\frac1N\sum_{l=1}^N\sum_{k=1}^Ky_k^{(l)}\log[\text{softmax}_k(\boldsymbol{x}^{(l)}\boldsymbol{W})]$$

其中$y_k^{(l)}$是$\boldsymbol{y}^{(l)}$的第$k$个元素。由独热编码的性质，这里每个样本实际上只被取了在正确类别上的概率，则整个损失函数的意义就是最大化所有样本在正确类别上的平均概率。

关于$\boldsymbol{w}_j$的梯度是：

$$\frac{\partial L(\boldsymbol{W})}{\partial\boldsymbol{w}_j}=\frac1N\sum_{l=1}^N\big(\text{softmax}_j\big(\boldsymbol{x}^{(l)}\boldsymbol{W}\big)-\boldsymbol{y}_j^{(l)}\big)\boldsymbol{x}^{(l)T}$$

若简记$\boldsymbol{W}=[\boldsymbol{w}_1, \boldsymbol{w}_2, \dots, \boldsymbol{w}_k]$梯度可以写为：

$$\frac{\partial L(\boldsymbol{W})}{\partial\boldsymbol{W}}=\frac1N\sum_{l=1}^N\boldsymbol{x}^{(l)T}\big(\text{softmax}\big(\boldsymbol{x}^{(l)}\boldsymbol{W}\big)-\boldsymbol{y}^{(l)}\big)$$

利用梯度下降进行对参数进行更新。

第三讲 从概率的角度看回归与分类

回归和分类的目标都是根据输入$\boldsymbol{x}$去预测输出$y$。之前都是利用确定的函数，直接得出预测值$\hat y$。从概率的角度，我们可以从条件概率的角度建模，在已知条件$\boldsymbol{x}$的情况下，得到$y$的分布，然后以均值（期望）作为预测值：

$$\hat y=\int y p(y|\boldsymbol{x})dy$$

或者概率最大的那个值作为预测值

$$\hat y =\arg \max_y p(y|\boldsymbol{x})$$

1、从概率的角度看回归

单变量的高斯分布：

$$p(z)-\frac{1}{\sqrt{2\pi \sigma^2}}\exp[-\frac{(z-\mu)^2}{2\sigma^2}]$$

其中$\mu$是平均数，$\sigma^2=E[(z-\mu)^2]$是方差

---

多变量的高斯分布：

$$p(\boldsymbol{z})=\frac{1}{(2\pi)^{D/2}|\boldsymbol{\Sigma}|^{1/2}}\exp\left\{-\frac{1}{2}(\boldsymbol{z}-\boldsymbol{\mu})^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{z}-\boldsymbol{\mu})\right\}$$

其中$D$是维度，$\boldsymbol{\mu}\in \R^D$是平均值向量，$\boldsymbol{\Sigma}\in \R^{D\times D}$是协方差矩阵

根据协方差矩阵，分布的形状不尽相同：

每一个协方差矩阵$\boldsymbol{\Sigma}$可以作分解：$\boldsymbol{\Sigma}=\boldsymbol{U \Lambda U}^T$。其中$\boldsymbol{U}$是正交矩阵，也即$\boldsymbol{UU}^T=\boldsymbol{I}$；$\boldsymbol{\Lambda}$是对角阵。

于是，记$\boldsymbol{z}'=\boldsymbol{U}^T\boldsymbol{z}, \boldsymbol{\mu}'=\boldsymbol{U}^T\boldsymbol{\mu}$，原来的分布可以重新写为：

$$p(\boldsymbol{z}')=\frac{1}{(2\pi)^{D/2}|\boldsymbol{\Lambda}|^{1/2}}\exp\left\{-\frac{1}{2}(\boldsymbol{z}'-\boldsymbol{\mu}')^{T}\boldsymbol{\Lambda}^{-1}(\boldsymbol{z}'-\boldsymbol{\mu}')\right\}$$

调整前后的对比：

---

对于回归问题，我们假设$y$的分布是一个正态分布（或者说$y$在真实值的基础上加上了一个高斯噪声）：

$$p(y|\boldsymbol{x};\boldsymbol{w})\sim \mathcal{N}(y;\boldsymbol{xw}, \sigma^2)$$

取其均值作为预测值：

$$\hat y=\boldsymbol{xw}$$

我们的目标是最大化对数似然概率：

$$\max_{\boldsymbol{w}} \log p(y|\boldsymbol{x};\boldsymbol{w})$$

这等价于：

$$\min_{\boldsymbol{w}}(y-\boldsymbol{xw})^2$$

与之前是一致的。

对于$N$个样本，假设他们是独立同分布的（i.i.d.），则他们的联合条件概率密度函数为：

$$p\big(y^{(1)},\cdots,y^{(N)}|\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}\big)=\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left[-\frac{1}{2}\frac{\big(y^{(i)}-\boldsymbol{x}^{(i)}w\big)^{2}}{\sigma^{2}}\right]$$

最大化其对数似然概率等价于最小化：

$$\sum_{i=1}^N(y^{(i)}-\boldsymbol{x}^{(i)}\boldsymbol{w})^2$$

仍然与之前一致。

2、从概率的角度看分类

考虑伯努利分布：

$$p(z)= \begin{cases} &\pi, &z=1\\ &1-\pi, &z=0 \end{cases}$$

其概率密度函数可以写为$p(z)=\pi^z(1-\pi)^{1-z}, z=0, 1$

对于二分类问题，假设其服从伯努利分布，则有：

$$p(y|\boldsymbol{x})=(\sigma(\boldsymbol{xw}))^y(1-\sigma(\boldsymbol{xw}))^{1-y}$$

其中$\pi=\sigma(\boldsymbol{xw}), y=0, 1$

目标仍然是最大化似然概率$\max \log p(y|\boldsymbol{x})$，这等价于最小化交叉熵，与之前的讨论一致。

---

对于多分类问题，同理。分布写为：

$$p(\boldsymbol{z})=\prod_{k=1}^K \pi_k^{z_k}$$

其中$\boldsymbol{z}$是一个独热编码向量，$\pi_k$是属于第$k$类的概率。

令$\pi_k=\text{softmax}_k(\boldsymbol{xW})$，则：

$$p(\boldsymbol{y}|\boldsymbol{x})=\prod_{k=1}^{K}[\text{softmax}_k(\boldsymbol{xW})]^{y_k}$$

最大化对数似然概率仍然等价于最小化交叉熵。

第四讲 非线性模型、过拟合与正则化

1、非线性模型

线性回归只对原本就是线性关系的变量效果较好；线性分类器的决策边界也只能是线性的。事实上，现实中线性的决策边界或者线性回归无法处理更复杂的情况。

一个基本的想法就是用基函数去非线性化原来的线性模型。

原来的线性回归可写为$f(x)=w_0+w_1x=[1, x]\boldsymbol{w}$。如果采用更复杂的基函数，则可以写为$f(x)=w_0+w_1x+w_2x^2+w_3x^3=\boldsymbol{\phi}(x)\boldsymbol{w}$

一般地，基函数模型可以写为：$f(\boldsymbol{x})=\boldsymbol{\phi}(\boldsymbol{x})\boldsymbol{w}=[\phi_1(\boldsymbol{x}), \phi_2(\boldsymbol{x}), \dotsm ,\phi_n(\boldsymbol{x})]\boldsymbol{w}$

基函数模型对$\boldsymbol{x}$不一定是线性的，但是对参数$\boldsymbol{w}$仍然是线性的。

---

经过非线性变换后，损失函数可以写为：

$$L(\boldsymbol{w})=\frac 1 N \Vert \boldsymbol{\phi}(\boldsymbol{X})\boldsymbol{w}-\boldsymbol{y}\Vert^2$$

其中

$$\boldsymbol{\phi}(\boldsymbol{X})= \begin{bmatrix} \boldsymbol{\phi}(\boldsymbol{x}^{(1)})\\ \vdots\\ \boldsymbol{\phi}(\boldsymbol{x}^{(N)}) \end{bmatrix}$$

最小化损失函数，最优参数为：

$$\boldsymbol{w}^*=(\boldsymbol{\phi}^T\boldsymbol{\phi})^{-1}\boldsymbol{\phi}^T\boldsymbol{y}$$

这就是将原来线性回归中的$\boldsymbol{X}$替换为$\boldsymbol{\phi}=\boldsymbol{\phi}\boldsymbol{(X)}$的结果。

---

分类问题中同理。交叉熵变为：

$$L(\boldsymbol{W})=-\frac1N\sum_{l=1}^N\sum_{k=1}^Ky_k^{(l)}\log[\text{softmax}_k(\boldsymbol{\phi}(\boldsymbol{x}^{(l)})\boldsymbol{W})]$$

梯度变为：

$$\frac{\partial L(\boldsymbol{W})}{\partial\boldsymbol{w}_j}=\frac1N\sum_{l=1}^N\big(\text{softmax}_j\big(\boldsymbol{\phi}^{(l)}\boldsymbol{W}\big)-\boldsymbol{y}^{(l)}\big)\boldsymbol{\phi}^{(l)T}$$

同样是将原来的$\boldsymbol{x}^{(l)}$替换为$\boldsymbol{\phi}^{(l)}=\boldsymbol{\phi}(\boldsymbol{x}^{(l)})$的结果

2、过拟合

基函数的维数越高，就能更好的拟合训练数据。但是相对的，在测试集上的表现就会越来越差。

模型在模式数据上的表现称为这个模型的泛化能力。一般来说，基函数的维数越多，这个模型的参数也就越多，模型越复杂。

不能仅仅依据模型在测试集上的表现来评价一个模型，其在泛化能力也十分重要。

---

可以将 20%~30%的训练集数据划分出来作为验证集。利用训练集的数据进行训练，然后再验证集上评估模型的泛化能力。选择在验证集上表现最好的模型。

当验证集上的错误率随着复杂度提升而下降时，称模型此时是欠拟合的；当验证集上的错误率随复杂度提升而提升时，称模型此时是过拟合的。

---

训练数据通常是比较少的，如果还划分一部分用于验证集，则没有足够的数据样本用于训练，此时可以采取K-fold 交叉验证。

也即把训练集分为 K 份，第 i 轮训练用第 i 份作为验证集，其他 K-1 份用于训练。

---

信息准则（Information Criteria） 用于评估模型的复杂度。

Akaike Information Criteria（AIC，赤池信息准则）：

$$\text{AIC}=2M-2\log(L)$$

其中$M$是模型的参数量，$L$是该模型下的最大似然。一般，AIC 越小，模型越好。

Bayesian Information Criteria（BIC）

$$\text{BIC}=M\log N-2\log (L)$$

其中$N$是训练数据数量。

这两个标准一般只能用于概率模型中，因为需要用到对数似然。

3、正则化

过拟合一般是由高阶项对应的参数过大导致的。我们引入正则项来平衡这些影响：

$$\tilde{L}(\boldsymbol{w})=L(\boldsymbol{w})+\lambda \Vert \boldsymbol{w}\Vert_2^2$$

其中$\lambda$是超参数，用于控制正则项的影响。利用 2 范数进行正则化的，称为$L_2$正则化。它将参数趋向于 0。

正则化后得到的模型曲线更平滑。

还有一种$L_1$正则化：

$$\tilde{L}(\boldsymbol{w})=L(\boldsymbol{w})+\lambda \Vert \boldsymbol{w}\Vert_1$$

这种正则化可以让参数变为 0（而不仅仅是趋向 0），所以经常趋向于得到松弛解。

第五讲 支持向量机

1、线性分类器的决策边界

之前的线性分类器的基础上加上一个偏置项，交叉熵损失函数变为：

$$L(\boldsymbol{w}, b)=-y\log(\sigma(\boldsymbol{w}^T\boldsymbol{x}+b)) -(1-y)\log(1-\sigma(\boldsymbol{w}^T\boldsymbol{x}+b))$$

损失函数最小值为 0，记使其为 0 的最优的$\boldsymbol{w}^*, b^*$，则$L(\boldsymbol{w}, b)=0$表示的超平面为：$\{\boldsymbol{w}|\boldsymbol{w}^{*T}\boldsymbol{x}+b^*=0\}$

这个超平面：

• 垂直于$\boldsymbol{w}^*$
• 到原点的距离是$-b^*/\Vert \boldsymbol{w}^* \Vert$

事实上，使得$L(\boldsymbol{w}, b)=0$的$\boldsymbol{w}^*, b^*$有很多个，对应的超平面也有很多个。我们希望找到一个对于陌生数据也能表现得很好的超平面。如下图，我们希望找到一个具有最大间隔的超平面。

2、线性最大间隔分类器

如何表示“间隔”呢？考虑某个数据点$\boldsymbol{x}$到超平面$\mathcal{H}$的距离。

先记$h(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b$

从原点到某个数据点$\boldsymbol{x}$的向量就是$\boldsymbol{x}$，有$\boldsymbol{x}=\boldsymbol{m}_1+\boldsymbol{m}_2$。其中$\boldsymbol{m}_2\perp \mathcal{H}$，则$\boldsymbol{m}_1$代表的向量一端恰好在$\mathcal{H}$上，所以有$h(\boldsymbol{m}_1)=0$

则：

$$h(\boldsymbol{x})=\boldsymbol{w}^T(\boldsymbol{m_1}+\boldsymbol{m}_2)+b=\boldsymbol{w}^T \boldsymbol{m}_2$$

又因为$\boldsymbol{m_2} \parallel \boldsymbol{w}$，所以：

$$\boldsymbol{m}_2=\Vert \boldsymbol{m}_2\Vert \frac{\boldsymbol{w}}{\Vert \boldsymbol{w}\Vert}$$

结合上面两式即得：

$$\Vert \boldsymbol{m}_2\Vert=\frac{h(\boldsymbol{x})}{\Vert \boldsymbol{w}\Vert}$$

所以对于正类的数据点$\boldsymbol{x}$，其到超平面的距离就是$h(\boldsymbol{x})/\Vert \boldsymbol{w}\Vert$；对于负类的数据点$\boldsymbol{x}$，其到超平面的距离就是$-h(\boldsymbol{x})/\Vert \boldsymbol{w}\Vert$。或者写成统一形式：

$$\frac{y h(\boldsymbol{x})}{\Vert \boldsymbol{w}\Vert}, y\in \{-1, 1\}$$

“间隔”取决于距离超平面最近的那个数据点：

$$\text{Margin}=\min_l \frac{y^{(l)}(\boldsymbol{w}^T\boldsymbol{x}^{(l)}+b)}{\Vert \boldsymbol{w}\Vert}$$

我们希望找到一个超平面使得间隔最大，也即希望求得：

$$\arg \max_{\boldsymbol{w}, b} \left\{\min_l \frac{y^{(l)}(\boldsymbol{w}^T\boldsymbol{x}^{(l)}+b)}{\Vert \boldsymbol{w}\Vert}\right\}$$

---

原问题是一个无约束的优化问题。假设$\boldsymbol{w}^*$以及$b$就是最优的参数，则$\widetilde{\boldsymbol{w} }=\kappa\boldsymbol{w}^*, \widetilde{b}=\kappa b$也是最优的参数（$\kappa\neq 0$）。

一定存在$\kappa$，使得$y^{(l)}(\kappa\boldsymbol{w}^{*T}\boldsymbol{x}^{(l)}+\kappa b^*)\geqslant 1, \forall l$，且保证至少存在一个$l$能使得等号成立。

所以原问题可以转化为一个等价的有约束问题，即求：

$$\arg \max_{\widetilde{\boldsymbol{w} }, \widetilde{b}} \left\{\min_l \frac{y^{(l)}(\widetilde{\boldsymbol{w} }^T\boldsymbol{x}^{(l)}+\widetilde{b})}{\Vert \widetilde{\boldsymbol{w} }\Vert}\right\}, s.t.\ y^{(l)}(\widetilde{\boldsymbol{w} }^T\boldsymbol{x}^{(l)}+\widetilde{b})\geqslant 1, \forall l$$

对于这个问题，因为存在某个$l$使得等号成立，所以有：

$$\min_l y^{(l)}(\widetilde{\boldsymbol{w} }^T\boldsymbol{x}^{(l)}+\widetilde{b})=1$$

优化目标变为：

$$\arg \max_{\widetilde{\boldsymbol{w} }, \widetilde{b}} \frac{1}{\Vert \widetilde{\boldsymbol{w} }\Vert}$$

这等价于：

$$\arg \min_{\widetilde{\boldsymbol{w} }, \widetilde{b}} \frac{1}{2}\Vert \widetilde{\boldsymbol{w} }\Vert^2$$

综上，求最大间隔的超平面等价于求解以下有约束的凸优化问题：

$$\arg \min_{\widetilde{\boldsymbol{w} }, \widetilde{b}} \frac{1}{2}\Vert \widetilde{\boldsymbol{w} }\Vert^2, s.t.\ y^{(l)}(\widetilde{\boldsymbol{w} }^T\boldsymbol{x}^{(l)}+\widetilde{b})\geqslant 1, \forall l$$

如果求得最优参数$\boldsymbol{w}^*, b^*$，则我们可以按照下式预测分类结果：

$$\hat y=\text{sign}(\boldsymbol{w}^{*T}\boldsymbol{x}+b^*)$$

---

经过转化后的这个凸优化问题可以利用拉格朗日乘子法求解，具体过程在人工智能笔记中有详细介绍。

简而言之，引入拉格朗日乘子$\boldsymbol{\alpha}$，构建拉格朗日函数，然后求解其对偶问题。利用数值方法，可以求得最优的$\boldsymbol{\alpha}^*$，然后再求得最优的$\boldsymbol{w}^*, b^*$。

分类器也可以等价地写为：

$$\hat y=\text{sign}\left(\sum_{l=1}^N\alpha^{(l)}y^{(l)}\boldsymbol{x}^{(l)T}\boldsymbol{x}+b^*\right)$$

可以证明，$\alpha^{(i)}$大部分都为 0，只有少部分不为 0。这些不为 0 的$\alpha^{(i)}$对应的数据点$\boldsymbol{x}^{(i)}$称为支持向量。也即下图中，恰好在间隔边界上的数据点。

3、软线性最大间隔分类器

线性最大间隔分类器有解的前提是数据是线性可分的。如果数据不是线性可分的，就需要引入软间隔。

也即约束变为：

$$y^{(l)}(\boldsymbol{w}^T\boldsymbol{x}^{(l)}+b)\geqslant 1-\xi^{(l)}$$

其中$\xi^{(l)}\geqslant 0$是一个松弛变量，用于表示最多能容忍的误差。我们希望同时最小化间隔和误差，所以优化目标变为：

$$\min_{\boldsymbol{w}, b, \boldsymbol{\xi}} \left(\frac{1}{2}\Vert \boldsymbol{w}\Vert^2+C\sum_{l=1}^N\xi^{(l)}\right)$$

其中$C$是惩罚因子，它表示了误差的权重。$C$取无穷时，就退化到上一个线性最大间隔分类器。

同样可以利用拉格朗日乘子法求解。最终的分类器的形式仍然是：

$$\hat y=\text{sign}\left(\sum_{l=1}^N\alpha^{(l)}y^{(l)}\boldsymbol{x}^{(l)T}\boldsymbol{x}+b^*\right)$$

4、核技巧

上述的分类器仍然是线性的，引入基函数后，可以得到非线性的分类器：

$$\hat y=\text{sign}\left(\sum_{l=1}^N\alpha^{(l)}y^{(l)}\boldsymbol{\phi}(\boldsymbol{x}^{(l)})^T\boldsymbol{\phi}(\boldsymbol{x})+b^*\right)$$

越高维的空间中，数据点之间的距离越大，也就越容易找到一个可行的“超平面”，所以我们希望变换后的特征空间 $\boldsymbol{\phi}(\boldsymbol{x})$ 尽可能高维。但是也不能过高，因为维度越高，计算量也就越大。

整个问题的难点在于计算$\boldsymbol{\phi}(\boldsymbol{x}^{(l)})^T\boldsymbol{\phi}(\boldsymbol{x})$，这在高维空间中的计算量是非常大的。核技巧就是用于解决这个问题的。

---

核函数是一个包含两个变量的函数$K(\boldsymbol{x}, \boldsymbol{x}')$，可以表示为两个向量的内积：

$$K(\boldsymbol{x}, \boldsymbol{x}')=\boldsymbol{\phi}(\boldsymbol{x})^T\boldsymbol{\phi}(\boldsymbol{x}')$$

Mercer 定理指出，如果一个函数$K(\boldsymbol{x}, \boldsymbol{x}')$是对称正定的，也即：

$$\int \int K(\boldsymbol{x}, \boldsymbol{x}')f(\boldsymbol{x})f(\boldsymbol{x}')d\boldsymbol{x}d\boldsymbol{x}'\geqslant 0, \forall f(\cdot)\in L^2$$

则一定存在一个特征空间$\boldsymbol{\phi}(\boldsymbol{x})$，使得$K(\boldsymbol{x}, \boldsymbol{x}')=\boldsymbol{\phi}(\boldsymbol{x})^T\boldsymbol{\phi}(\boldsymbol{x}')$

一个最常用的核函数是高斯核函数：

$$K(\boldsymbol{x}, \boldsymbol{x}')=\exp\left(-\frac{\Vert \boldsymbol{x}-\boldsymbol{x}'\Vert^2}{2\sigma^2}\right)$$

其对应的特征空间是无穷维的：

$$\boldsymbol{\phi}(x)=e^{-x^2/2\sigma^2}\left[1, \sqrt{\frac{1}{1!\sigma^2}}x, \sqrt{\frac{1}{2!\sigma^4}}x^2, \dots\right]^T$$

所以利用核技巧，原来的分类器可以写为：

$$\hat y=\text{sign}\left(\sum_{l=1}^N\alpha^{(l)}y^{(l)}K(\boldsymbol{x}^{(l)}, \boldsymbol{x})+b^*\right)$$

5、与逻辑回归的联系

记$h^{(l)}=\boldsymbol{w}^T\boldsymbol{x}^{(l)}+b$

逻辑回归中，引入了正则项后，最终的优化目标是最小化：

$$L(\boldsymbol{w}, b)=\frac{-1}{N}\sum_{l=1}^N \left[y^{(l)}\log(\sigma(h^{(l)}))+(1-y^{(l)})\log(1-\sigma(h^{(l)}))\right]+\lambda\Vert \boldsymbol{w}\Vert^2$$

注意，支持向量机中的$y^{(l)}\in \{-1, 1\}$，所以单个数据点的损失应该为：

$$L(\boldsymbol{w}, b)= \begin{cases} -\log(\sigma(h)), &y=1\\ -\log(1-\sigma(h))=-\log(\sigma(-h)), &y=-1 \end{cases}$$

也即有：

$$L(\boldsymbol{w}, b)=\log(\sigma(y^{(l)}h^{(l)}))$$

所以按照支持向量机中标签的定义，逻辑回归的损失函数可以简单地写为：

$$L(\boldsymbol{w}, b)=\frac{-1}{N}\sum_{l=1}^N \log(\sigma(y^{(l)}h^{(l)}))+\lambda\Vert \boldsymbol{w}\Vert^2=\frac{1}{N}\sum_{l=1}^N \log(1+\exp(-y^{(l)}h^{(l)}))+\lambda\Vert \boldsymbol{w}\Vert^2$$

若记$E_{LR}(z)=\log(1+\exp(-z))$，所以逻辑回归的损失函数也可以写为：

$$L(\boldsymbol{w}, b)=\frac{1}{N}\sum_{l=1}^N E_{LR}(y^{(l)}h^{(l)})+\lambda\Vert \boldsymbol{w}\Vert^2$$

---

在理想分类器中，对于单个数据点，可以这样定义损失函数（0-1 Loss）：

$$L(\boldsymbol{w}, b)= \begin{cases} 0, &y^{(l)}h^{(l)}>0\\ 1, &y^{(l)}h^{(l)}\leqslant 0 \end{cases}$$

若函数$E_{Ideal}(z)$满足：

$$E_{Ideal}(z)= \begin{cases} 0, &z>0\\ 1, &z\leqslant 0 \end{cases}$$

于是整个数据集的损失函数可以写为：

$$L(\boldsymbol{w}, b)=\frac{1}{N}\sum_{l=1}^N E_{Ideal}(y^{(l)}h^{(l)})+\lambda\Vert \boldsymbol{w}\Vert^2$$

---

对于线性最大间隔分类器，我们定义：

$$E_{SVM}(z)= \begin{cases} 0, &z\geqslant 0\\ +\infty, &z<0 \end{cases}$$

则也可以把优化目标写成类似的形式：

$$L(\boldsymbol{w}, b)=\frac{1}{N}\sum_{l=1}^N E_{SVM}(y^{(l)}h^{(l)}-1)+\frac 1 2\Vert \boldsymbol{w}\Vert^2$$

---

而线性软最大间隔分类器，定义：

$$E_{Soft}(z)=\max(0, 1-z)$$

这种损失就是Hinge Loss。

由约束条件，有$y^{(l)}h^{(l)}\geqslant 1-\xi^{(l)}$，也即$\xi^{(l)}\geqslant 1-y^{(l)}h^{(l)}$，当$\xi^{(l)}$最小时，该约束取等号。又因为有$\xi^{(l)}\geqslant 0$，所以有：

$$\min \sum_{l=1}^N \xi^{(l)}=\min \sum_{l=1}^N \max(0, 1-y^{(l)}h^{(l)})$$

于是优化目标就可以写为：

$$\begin{split} L(\boldsymbol{w}, b) &=\frac{C}{N}\sum_{l=1}^N \xi^{(l)}+\frac 1 2\Vert \boldsymbol{w}\Vert^2 \\ &=\frac{1}{N}\sum_{l=1}^N E_{Soft}(y^{(l)}h^{(l)})+\lambda\Vert \boldsymbol{w}\Vert^2 \end{split}$$

---

由上可见，逻辑回归、理想分类器、线性最大间隔分类器、线性软最大间隔分类器的损失函数都可以写为类似的形式，差别仅在于损失函数的定义。

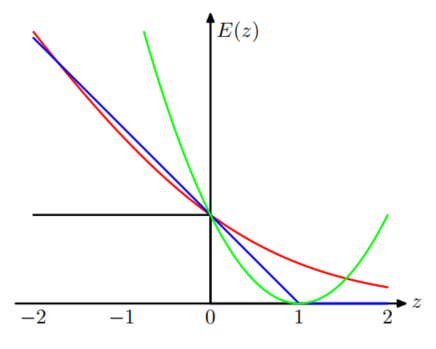
下图是这几种分类器的损失函数的图像：

上面的四种损失函数依次对应红、黑、绿、蓝四条线。

第六讲 神经网络

1、神经网络

非线性模型在许多应用上取得了良好的效果。目前提到的非线性化模型的方法有两种：

• 利用基函数$\boldsymbol{\phi}(\cdot)$来进行特征变换
• 利用核技巧，可以理解为一个无限维的基函数变换

以上两种方法中，基函数（的参数）都是固定的，不能根据数据的特征进行调整。上述的两种方法可以用下图表示：

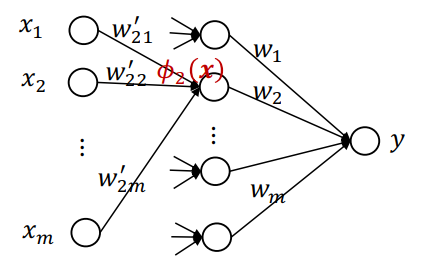
设想让“非线性化”过程中的参数是可学习的（可变的）：

其中$w_{21}', w_{22}', \dots, w_{2m}'$都是可变的。

一般地，令$\phi_i(\boldsymbol{x})=a(\sum_{l=1}^m w_{i l}'x_l)$，其中$a(\cdot)$是激活函数。激活函数一定要有（而且不能是线性函数），否则最终$y$相对于$x$还是线性的。

于是上图的输出可以写为：

$$\hat{y}=\boldsymbol{w}_2^T a(\boldsymbol{W}_1 x)$$

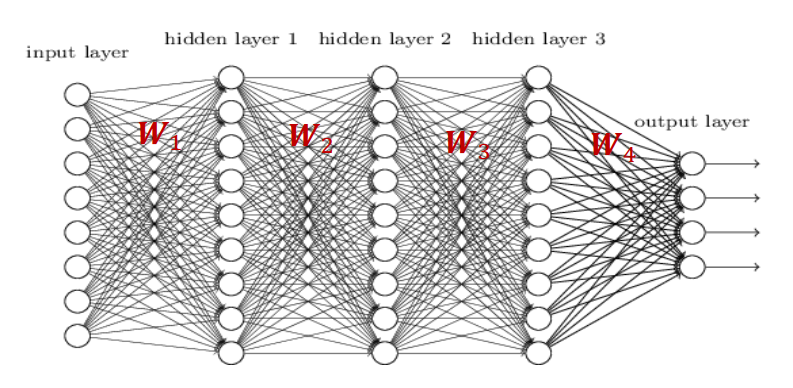
在此基础上，不断增加堆叠的层数：

一个$L$层的神经网络可以写为：

$$\hat{y}=\boldsymbol{W}_La(\cdots a(\boldsymbol{W}_2a(\boldsymbol{W}_1 \boldsymbol{x})))$$

其中最外层到底是矩阵$\boldsymbol{W}_L$还是一个向量$\boldsymbol{w}_L$取决于需要怎样的输出。如果是回归问题，输出是一个实数，那就是后者；如果是分类问题，输出是一个向量，那就是前者，当然最后需要再套一个$\text{softmax}$函数。

---

介绍四种常见的激活函数：

$$\text{sigmoid}(x)=\frac{1}{1+e^{-x}}$$

• 易有梯度消失现象
• 只输出正值
• 指数函数的计算代价高

$$\text{tanh}(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$

• 易有梯度消失现象
• 指数函数的计算代价高
• 同时输出正值和负值

$$\text{ReLU}(x)=\max(0, x)$$

• 在$x>0$时没有梯度消失现象；$x<0$时梯度为 0
• 计算效率高
• 只输出正值

$$\text{Leaky Relu}(x)=\max(0.1, x)$$

• 对所有的$x$都没有梯度消失现象
• 计算效率高

---

给定训练集$\mathcal{D}=\{(\boldsymbol{x}_i, y_i)\}$，回归问题的损失函数可以写为：

$$L=\frac 1 N\sum_{(\boldsymbol{x}, y)\in \mathcal{D}}|y-\hat{y}|^2$$

多分类问题的损失函数可写为：

$$L=-\frac 1 N\sum_{(\boldsymbol{x}, y)\in \mathcal{D}}\sum_{k=1}^K y_k\log \hat{y_k}$$

2、反向传播

同样，我们使用梯度下降法来更新参数，需要计算$\frac{\partial L}{\partial \boldsymbol{W}_l}$。整个网络中有大量的参数，我们考虑递归的方式来求每个参数的梯度。

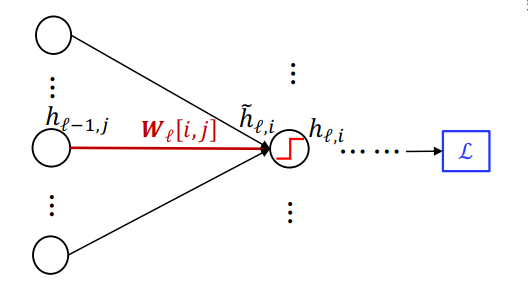
首先考虑一个局部：

这里$W_{l, i, j}$是第$l$层的参数中，第$l$个隐藏层第$i$个节点的第$j$个参数。则有：

$$\begin{split} \frac{\partial L}{\partial W_{l, i, j}}&=\frac{\partial L}{\partial h_{l, i}}\frac{\partial h_{l, i}}{\partial \tilde{h}_{l, i}}\frac{\partial \tilde{h}_{l, i}}{\partial W_{l, i, j}}\\ &=\frac{\partial L}{\partial h_{l, i}}\cdot a'(\tilde{h}_{l, i})\cdot h_{l-1, j} \end{split}$$

所以计算对$W_{l, i, j}$梯度的关键是计算出对$h_{l, i}$的梯度。

下面看计算对$h_{l, i}$的梯度：

有：

$$\begin{split} \frac{\partial L}{\partial h_{l, i}}&=\sum_{j=1}^m\frac{\partial L}{\partial h_{l+1, j}}\frac{\partial h_{l+1, j}}{\partial h_{l, j}}\\ &=\sum_{j=1}\frac{\partial L}{\partial h_{l+1, j}}\cdot a'(\tilde{h}_{l+1, j})\cdot W_{l+1, j, i} \end{split}$$

所以计算对对$h_{l, i}$的梯度关键是计算出下一层的，对$h_{l+1, j}$的梯度。

综上，可以从后往前，一步步的计算出对所有参数的梯度。梯度是从后往前传播的，于是把这个过程称之为反向传播。

利用反向传播计算参数的过程总共可以分为两步

1. 计算：

   $$\frac{\partial L}{\partial \boldsymbol{h}_l}=\boldsymbol{W}_{l+1}^T({\boldsymbol{a}}'_{l+1}\odot \frac{\partial L}{\partial \boldsymbol{h}_{l+1}}),{\boldsymbol{a}}'_{l+1}=[a'(\tilde{h}_{l+1, 1}), a'(\tilde{h}_{l+1, 2}), \cdots, a'(\tilde{h}_{l+1, m})]^T$$

2. 计算：

   $$\frac{\partial L}{\partial \boldsymbol{W}_l}=({\boldsymbol{a}}'_{l}\odot \frac{\partial L}{\partial \boldsymbol{h}_{l}})\boldsymbol{h}_{l-1}^T$$

3、各种类型的神经网络

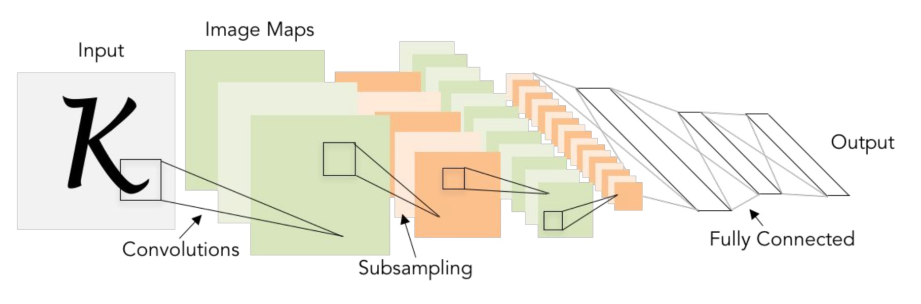
3.1、CNN

Convolutional Neural Networks，卷积神经网络

上述的普通全连接网络（多层感知机，MLP）有以下缺点：

• 参数数量巨大，容易过拟合
• 没有考虑数据数据中潜在的结构信息

CNN 就是一种可以利用图片/视觉信息中潜在结构的网络。

---

二维图像可以理解为二维矩阵，用过滤器（Filter）对原始图像做卷积，“提取”出特征信息：

CNN 中，基本的结构是卷积层+ReLU+池化层：

这种结构可以多次堆叠。其特点是：

• 减少维度
• 使模型非线性化
• 保留重点特征

更详细生动的解释可以查看人工智能笔记。

---

下面介绍几种具体的 CNN：

LeNet，其结构是卷积层+池化层+卷积层+池化层+全连接层+全连接层：

AlexNet 则结构更多更复杂，包括五个卷积层和三个全连接层：

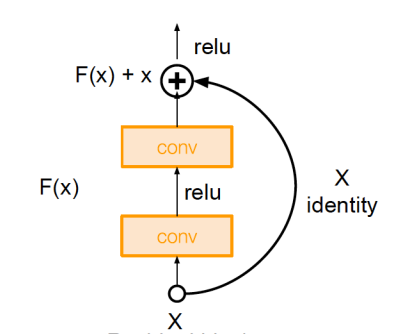
ResNet 则有 152 层。层数不是越多越好，层数越多，意味着参数越多，也越难以训练。ResNet 还引入了残差连接（Shortcut Connection），创建了一些直接让相隔的层相连的连接。如下图中的弧线就是残差连接：

3.2、RNN

Recurrent Neural Network，循环神经网络，其核心思想是会考虑网络的隐藏状态，使得模型能够“记忆”之前的信息。

每个新的输入都会更新隐藏状态，输出要同时考虑输入和上一个隐藏状态。这样就能够考虑到前后数据潜在的依赖关系

---

多到多的 RNN：

应用的例子有语言模型、视频帧分类等

---

多到一的 RNN：

应用的例子有序列分类、情感分析等

---

一到多的 RNN：

应用的例子有图片内容分析等

---

多到一（编码器）+一到多（解码器）的 RNN：

应用的例子有机器翻译、语句特征提取等。

---

LSTM，长短期记忆网络，引入了一个特殊的结构来精细控制记忆的内容：

通过引入门控机制来控制信息流，是一种有效解决梯度消失问题并捕捉长期依赖关系的循环神经网络。

第七讲 优化算法与训练技术

1、优化算法

1.1、随机梯度下降

Stochastic Gradient Descent，SGD。基本思想是使用部分样本计算损失，然后继续梯度下降。

用数学形式来表达即：

$$\boldsymbol{w}_{t+1}= \boldsymbol{w}_t-\eta \nabla L(\boldsymbol{x}, y; \boldsymbol{w}_t)$$

其中$\eta$是学习率，$\nabla L(\boldsymbol{x}, y; \boldsymbol{w}_t)$是部分样本的平均损失。

SGD 的问题是，非常容易陷入局部最优，且解空间中一些病态弯曲（pathological curvature）造成收敛缓慢，如下图：

SGD 的路线会是图中的折线，而不是我们期望的直线。

1.2、SGD+Momentum

SGD+Momentum 是在 SGD 的基础上引入了动量项，其更新公式为：

$$\begin{align*} \boldsymbol{v}_{t}&=\rho \boldsymbol{v}_{t-1}+\nabla L(\boldsymbol{x}, y;\boldsymbol{w}_t)\\ \boldsymbol{w}_{t+1}&=\boldsymbol{w}_t-\eta \boldsymbol{v}_t \end{align*}$$

其中$\rho\in(0, 1)$是动量因子，常选择的值是 0.9、0.95、0.99。

这里的动量项与物理学中的动量类似。可以想象，一个小球从坡上滚下，首先由于有重力，下坡速度越来越快，动量越来越大；其次如果遇到一个上坡，积累的动量有益于克服上坡的阻力帮其脱出。也就是说，引入动量项可以加速收敛，避免陷入局部最优。

1.3、RMSProp

Root Mean Square Propagation，均方根传播。其更新公式为：

$$\begin{align*} \boldsymbol{s}_t&=\rho \boldsymbol{s}_{t-1}+(1-\rho)(\nabla L(\boldsymbol{x}, y; \boldsymbol{w}_t))^2\\ \boldsymbol{w}_{t+1}&=\boldsymbol{w}_t-\eta\nabla L(\boldsymbol{x}, y; \boldsymbol{w}_t)\oslash \sqrt{\boldsymbol{s}_t} \end{align*}$$

其中$\oslash$表示两个相同形状的矩阵对应元素相除，$\boldsymbol{s_t}$是之前梯度的平方的加权。$\oslash \sqrt{\boldsymbol{s}_t}$这个操作相当于将加权梯度进行了归一化，拉到相同的水平，这样可以避免病态弯曲（两边不会那么陡峭）。由于加权梯度还包含了之前的信息，相当于将之前的信息“传递”过来，这也是算法名字的来源。

将更新式子展开后即可发现，在衰减因子的作用下，时间越早的梯度对更新的影响越小，这也是常见的思想。

1.4、Adam

Adaptive Moment Estimation 的缩写，是一种结合了 Momentum 和 RMSProp 的优化算法。其更新公式为：

$$\begin{align*} \boldsymbol{m}_t&=\beta_1\boldsymbol{m}_{t-1}+(1-\beta_1)\nabla L(\boldsymbol{x}, y; \boldsymbol{w}_t)\\ \boldsymbol{s}_t&=\beta_2\boldsymbol{s}_{t-1}+(1-\beta_2)(\nabla L(\boldsymbol{x}, y; \boldsymbol{w}_t))^2\\ \boldsymbol{w}_{t+1}&=\boldsymbol{w}_t-\eta\boldsymbol{m}_t\oslash \sqrt{\boldsymbol{s}_t} \end{align*}$$

其中$\boldsymbol{m}_t$是过去梯度的移动平均。当$\beta_1=0$时，Adam 就退化为了 RMSProp。

参数的一组常见设置是$\beta_1=0.9, \beta_2=0.999, \eta=0.001$

2、训练技巧

2.1、预处理

一些经常使用的数据处理方法包括：

• 中心化：例如同时减去均值
• 归一化：每个维度的数据都除以标准差
• 白化（Whitening）数据

下图直观地展示了这三种方法的效果：

---

下面讨论中心化和归一化数据的有效性。考虑一个线性回归问题，其损失函数是：

$$L(\boldsymbol{w})=\frac 1 n \Vert \boldsymbol{X}\boldsymbol{w}-\boldsymbol{y}\Vert^2$$

由于各个特征值可能数量级不同，则不同维度的相同步进，对损失函数值的影响会有很大不同，这导致收敛缓慢。中心化和正则化就是在将不同维度的特征值调整到相同的数量级。

2.2、初始化

从固定高斯分布随机取样来初始化神经网络中各层的权重，尤其是在较浅的神经网络（层数小于 8）时，会取得较好的效果。一个常用的高斯分布是：

$$\boldsymbol{w}\sim N(0, 0.01^2)$$

如果激活函数使用的是$\text{ReLU}$，则可以使用截断的高斯分布，其是通过将标准高斯分布中超出特定范围的值的概率设为零，并对剩余部分进行归一化处理得到的。：

$$\boldsymbol{w}\sim N_T(0, 0.01^2)$$

---

如果神经网络较深，可以通过对以下高斯分布进行采样，来对计算出第$i$层节点值要用到的参数初始化：

$$\boldsymbol{w}\sim N(0, \sigma_i^2)$$

其中$\sigma_i$是第$i-1$层的神经元个数的倒数的平方根。

2.3、Dropout

基本思想是在前向传播的过程中，随机地“丢弃一些节点”，也即将一些节点的输出设置为 0。这样可以有效防止过拟合，尤其是在深度神经网络中。

将模型用于测试时，我们一般希望对于相同的输入能得到相同的输出，所以此时要关掉 Dropout。

另一个问题出现了，模型中的参数，是适合训练时的数据的。而训练时数据由于有 Dropout，每层的输入都会小于原始输入。所以测试时，每层的输入也要加上 Dropout 的概率：

$$\boldsymbol{h}_{l+1}=\sigma(p \boldsymbol{W}_l \boldsymbol{h}_l)$$

2.4、批量归一化

Batch Normalization，BN。其基本思想是在每一层的输入上进行归一化。

一个好的初始化可以让模型一开始在解空间中处于一个正常的位置，但是随着训练的进行，初始化的效果越来越弱，最后还是取决于训练过程的好坏。

一种解决方法就是引入 BN 层，将某一个隐藏层的输出$\{\boldsymbol{h}_l^{(i)}\}_{i=1}^N$变为标准正态分布：

$$\hat{\boldsymbol{h}}_l^{(i)}=(\boldsymbol{h}_l^{(i)}-\boldsymbol{\mu}_l)\oslash \boldsymbol{\sigma}_l$$

其中$\boldsymbol{\mu}_l, \boldsymbol{\sigma}_l^2$分别是$\boldsymbol{h}_l^{(i)}$的均值和标准差。进一步地，可以引入两个可学习的参数$\boldsymbol{\gamma}_l, \boldsymbol{\beta}_l$，来调整归一化后的值：

$$\tilde{\boldsymbol{h}}_l^{(i)}=\boldsymbol{\gamma}_l\odot\hat{\boldsymbol{h}}_l^{(i)}+\boldsymbol{\beta}_l$$

其中$\odot$是对应元素相乘。根据所有样本计算均值和标准差代价太大，一般用某一个小批次的均值和方差来近似。

---

同样考虑利用模型进行测试时，输出依赖于每个小批次的均值和方差，导致输出不稳定。一般有两个解决方法：

• BN 层统一采用整个训练集的均值和方差
• 用移动平均来估计均值和方差

---

最后，整个 BN 层的计算过程可以写为：

$$\text{BN}(\boldsymbol{h}_l)=\boldsymbol{\gamma}_l\odot(\boldsymbol{h}_l-\boldsymbol{\mu}_l)\oslash \boldsymbol{\sigma}_l+\boldsymbol{\beta}_l$$

2.5、超参数调整

学习率等超参数的调整也不是盲目的，有一些一般性的方法：

1. 首先尝试在许多问题上表现优异的超参数
2. 根据训练结果逐渐来调整

不同超参数表现出来的 loss 曲线如下图：

第八讲 决策树

Decision Tree，DT。

决策树也是一种分类器，但是与之前提到的线性回归/逻辑回归/支持向量机等分类器不同，决策树分类器是通过建立一个树形结构来进行分类。

1、基本概念

决策树中：

1. 根节点和内部节点表示一个属性（特征）
2. 叶子节点对应一个（最终被划分为的）类别
3. 边对应某个属性值

利用决策树进行分类，就是从根节点开始，根据属性值逐步向下，直到到达叶子节点。叶子节点的类别就是最终的分类结果。

学习出一个好的决策树，要考虑：

• 每个节点上用哪个属性进行划分（可以重复使用属性）
• 某个节点引出哪些边（如何划分属性值）
• 何时停止拓展决策树

2、选择属性的标准

生活中，我们对物体进行分类，一般会从最明显的特征入手，或者说从“包含最多信息”的特征入手，在决策树中也是如此。

---

我们先来介绍熵（Entropy）的概念，它是对随机变量的不确定性的度量。给定一个随机变量$Z\sim p(z)$，则其熵是：

$$H(Z)=-\sum_{z\in \mathcal{Z}}p(z)\log p(z)$$

其中$\mathcal{Z}$是随机变量$Z$可能取值的集合。

熵越大，变量取值的不确定性越大。如果变量在各种情况下取值都是相同的，则不能够通过这个变量来区分不同的情况，也即熵最大；如果变量在各种情况下取值都是不同的，则可以通过这个变量来区分不同的情况，也即熵最小。一句话：分布越平坦（均匀），熵越大。

---

条件熵是在给定一个随机变量$Y$的情况下，另一个随机变量$Z$的熵：

$$H(Z|Y)=\sum_{y\in \mathcal{Y}}p(Y=y)H(Z|Y=y)$$

我们总有$H(Z)\geqslant H(Z|Y)$，可以这样直观的理解：获取额外信息（$Y$的取值）后，把握一般都会变大，对$Z$的不确定性会减小。

---

最终我们引出信息增益（Information Gain）的概念。$Y$带来的信息增益$IG(Y)$，是知道随机变量$Y$取值，使另一个随机变量$Z$的熵减少的程度：

$$IG(Y)=H(Z)-H(Z|Y)$$

3、构建决策树

从根节点开始，我们计算知道各个属性对确定最后分类结果带来的信息增益，选择信息增益最大的属性作为根节点。

接下来，根据根节点各个属性的取值，将数据集划分为若干个子集，对每个子集递归地重复上述过程，用其他属性来构建子树。

当某个节点的所有样本都属于同一类别时，停止拓展。

还有其他可能的停止拓展的条件：所有属性都已使用过、树达到最大深度、信息增益值小于某个阈值等。

---

树过大或者过复杂时，容易过拟合，可以通过剪枝来解决这个问题。

利用验证集，可以在构建过程中或者构建结束后使用下面的策略：

• 减去某个节点不影响验证集的准确率
• 减去对验证集准确率提升最小的节点
• 验证集上的准确率开始下降即停止扩展

第九讲 集成学习

训练单个的，在所有数据上都表现优异的分类器（Strong Classifier）是困难的。但是，如果我们能够训练多个较弱的分类器（Weak Classifier），虽然它们每一个单拿出来在所有数据集上表现一般，但是对某一部分数据集表现优异，那么我们就可以通过用适当的方法将这些弱分类器组合起来，得到一个强分类器。这就是集成学习（Ensemble Learning）的基本思想。

主要要解决两个问题：

• 如何构建弱分类器
• 如何将弱分类器组合起来

弱分类器有很多种类，可以是决策树、SVM、神经网络等。

组合方式有两大类，无权的和加权的。

1、Bagging

Bootstrap Aggregating，自举汇聚法。

我们无法预知怎样划分数据，然后再在上面训练弱分类器并组合能取得最好的效果。可以转换思路，可以训练一些预测误差相互独立的弱分类器，这样相当于考虑不同方面的特征，最后再将这些弱分类器组合起来。

为了实现这一点，从原始数据集中随机取样出若干个大小相同的子集，然后在每个子集上训练一个弱分类器，最后将这些弱分类器组合起来。Bagging 中，最后利用弱分类器组合的方式是多数通过（Majority Voting），即对于每个样本，所有弱分类器投票，预测结果是得票最多的类别；或者对于回归问题，用所有弱分类器输出的平均值。可见 Bagging 是一种无权的组合方式。

这种方式下，各个弱分类器的误差可能还是有较大的相关性，我们可以进一步增加随机性。例如，如果弱分类器采用的是决策树，我们可以在构建决策树是，只使用随机地抽取的部分属性。这样每个决策树的形状都不尽相同，是一片随机森林（Random Forest）。

2、Boosting

这种方法的基本思想是，每次训练一个弱分类器，对于被误分类的样本，给予其更大的权重，然后投入到下一个弱分类器的训练中。最后将所有弱分类器带权组合起来。

具体有 AdaBoost（Adaptive Boosting）算法：

1. 初始化样本权重$w_i^{(0)}=\frac 1 N, i=1, 2, \cdots, N$
2. 对于第$k$轮迭代，训练一个分类器$h_k(\boldsymbol{x})$，用带权$\boldsymbol{w}^{(k-1)}$的样本
3. 训练结束后，计算错误率：

   $$\epsilon_k=\frac{\sum_{i=1}^N w_i^{(k-1)}I(h_k(\boldsymbol{x}_i)\neq y_i)}{\sum_{i=1}^N w_i^{(k-1)}}$$

   也即是被误分类的样本的权重之和占所有样本权重之和的比例
4. 该分类器在最终组合中的权重为

   $$\alpha_k=\frac 1 2 \ln \frac{1-\epsilon_k}{\epsilon_k}$$

5. 更新样本权重，用于下一轮训练：

   $$w_i^{(k)}=w_i^{(k-1)}\exp(-\alpha_k y_i h_k(\boldsymbol{x}_i))$$

由上述训练过程可见，误分类的样本权重会增大，正确分类的样本权重会减小，这样可以使得下一个弱分类器更关注于误分类的样本，这是一个增强的过程。同时还可以发现，最后的组合是带权的，与弱分类器的表现有关。

一个典型的误分类率曲线如下图所示：

---

考虑定义一个指数损失函数：

$$L(\boldsymbol{w})=\sum_{i=1}^N \exp(-y_i h(\boldsymbol{x}_i))$$

其中$h(\boldsymbol{x}_i)$是组合分类器：

$$h(\boldsymbol{x})=\sum_{i=1}^K \alpha_i h_i(\boldsymbol{x})$$

可以证明，AdaBoost 算法等价于在最小化指数损失函数。

第十讲 PCA

Principal Component Analysis，主成分分析。

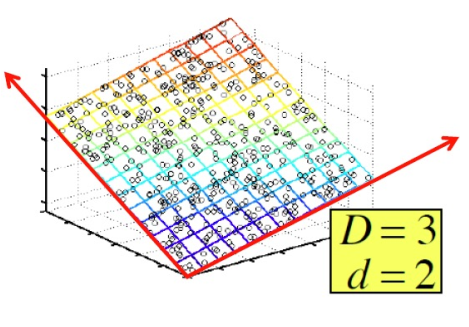
现实问题中，许多数据的维度都是巨大的，如果直接拿来计算，代价非常高。而且，数据的维度往往是冗余的，经常出现高维数据驻留在近似的低维空间的情况，如下图：

原始数据虽然是三维的，但近似可以认为都在一个二维平面上。

所以如果我们能找到数据分布的主要方向，就能用较少的维度来表示数据，从而节省计算资源。

1、角度一——最小化误差

由于我们抛弃了一些维度，误差是客观存在的，但是我们希望重建后数据与原始数据的误差尽可能小。

如果给定一组正交基，也即一组向量$\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_M$满足：

$$\boldsymbol{u}_i^T\boldsymbol{u}_j=\delta_{i, j}=\begin{cases}1, & i=j\\ 0, & i\neq j \end{cases}$$

在这组正交基张成的空间中，某个向量$\boldsymbol{x}$的最佳近似是：

$$\tilde{\boldsymbol{x}}=\sum_{i=1}^M \alpha_i\boldsymbol{u}_i$$

其中$\alpha_i=\boldsymbol{u}_i^T\boldsymbol{x}$。

这是因为最小化误差等价于：

$$\min \Vert \boldsymbol{x}-\tilde{\boldsymbol{x}}\Vert^2=\min \Vert \boldsymbol{x}-\sum_{i=1}^M \alpha_i\boldsymbol{u}_i\Vert^2=\min (\Vert \boldsymbol{x}\Vert^2-\sum_{i=1}^M \alpha_i \boldsymbol{u}_i^T\boldsymbol{x}+\sum_{i=1}^M \alpha_i^2)$$

这是一个凸优化问题，其解就是$\alpha_i=\boldsymbol{u}_i^T\boldsymbol{x}$。

---

接下来就是确定一组正交基，能够最小化这个最小的误差。一般，我们处理$\boldsymbol{x}-\overline{\boldsymbol{x}}$，而不是直接处理$\boldsymbol{x}$，其中$\overline{\boldsymbol{x}}$是整个数据集的均值。

我们的目标即是最小化整个数据集的平均重建误差：

$$E=\frac 1 N \sum_{i=1}^N \Vert (\boldsymbol{x}_i-\overline{\boldsymbol{x}})-\tilde{\boldsymbol{x}}_i\Vert^2$$

当然，我们已知$\alpha_{i, j}=\boldsymbol{u}_j^T(\boldsymbol{x}_i-\overline{\boldsymbol{x}})$，所以：

$$E=\frac 1 N \sum_{i=1}^N \Vert \boldsymbol{x}_i-\overline{\boldsymbol{x}}\Vert^2-\sum_{i=1}^M \boldsymbol{u}_i^T \frac 1 N \sum_{j=1}^N (\boldsymbol{x}_i-\overline{\boldsymbol{x}})(\boldsymbol{x}_i-\overline{\boldsymbol{x}})^T\boldsymbol{u}_i$$

其中$\frac 1 N \sum_{j=1}^N (\boldsymbol{x}_i-\overline{\boldsymbol{x}})(\boldsymbol{x}_i-\overline{\boldsymbol{x}})^T$是协方差矩阵，是对称的，记为$\boldsymbol{S}$。

则整个误差最终可以写成下面的形式：

$$E=\frac 1 N \Vert \boldsymbol{X}-\overline{\boldsymbol{X}}\Vert_F^2-\frac 1 N\sum_{i=1}^M \boldsymbol{u}_i^T\boldsymbol{S}\boldsymbol{u}_i$$

可以证明，与其等价的约束问题：

$$\max_{\boldsymbol{u}_i} \sum_{i=1}^M \boldsymbol{u}_i^T\boldsymbol{S}\boldsymbol{u}_i\quad\text{s.t.} \boldsymbol{u}_i^T\boldsymbol{u}_i=\delta_{i, j}$$

的解是$\boldsymbol{S}$从大到小排序前$M$个特征向量。由于$\boldsymbol{S}\in \mathbb{R}^{D\times D}$是实对称矩阵，所以其一定存在$D$个相互正交的特征向量。

2、角度二——最大化方差

另一个角度是最大化重建数据的方差。可以想象，把面上数据投影到一条线上，如果所有的数据都集中在线上某个点附近，则几乎无法区分数据，携带的信息很少；如果数据比较松散地分布在较大的范围内，容易区分出每个点，携带的信息就比较多。

由方差的定义，可以写出在某个方向$\boldsymbol{u}_j$上的整个数据集方差：

$$V=\frac 1 N \sum_{i=1}^N (\boldsymbol{u_j}^T(\boldsymbol{x}_i-\overline{\boldsymbol{x}}))^2=\boldsymbol{u}_j^T\boldsymbol{S}\boldsymbol{u}_j$$

这与我们在上一个角度得到的形式是一样的。

3、角度三——奇异值分解

一个矩阵$\boldsymbol{A} \in \mathbb{R}^{M\times N}$可以做奇异值分解：

$$\boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^T$$

其中$\boldsymbol{U}=[\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_M]\in \mathbb{R}^{M\times M}$和$\boldsymbol{V}=[\boldsymbol{v}_1, \boldsymbol{v}_2, \cdots, \boldsymbol{v}_N]\in \mathbb{R}^{N\times N}$是正交矩阵。$\boldsymbol{u}_i$和$\boldsymbol{v}_i$分别是$\boldsymbol{A}\boldsymbol{A}^T$和$\boldsymbol{A}^T\boldsymbol{A}$的特征向量。$\boldsymbol{\Sigma}$是一个对角矩阵，对角线上的元素是奇异值。

由于$\boldsymbol{\Sigma}$只有对角线上有非零值，原矩阵$\boldsymbol{A}$可以表达为：

$$\boldsymbol{A}=\sum_{i=1}^r \Sigma_{i, i}\boldsymbol{u}_i\boldsymbol{v}_i^T=\boldsymbol{U}'\boldsymbol{\Sigma}'\boldsymbol{V}'$$

如果取$\boldsymbol{A}=\boldsymbol{X}-\overline{\boldsymbol{X}}$，则有$\boldsymbol{A}\boldsymbol{A}^T=N\boldsymbol{S}$，$\boldsymbol{A}\boldsymbol{A}^T$的特征向量就是$\boldsymbol{S}$的特征向量。

综上可见，三个角度的 PCA 都是等价的。

第十一讲 K-means 聚类

给定一组数据$\{\boldsymbol{x}_i\}$，聚类就是将数据分成若干个簇：

簇内的数据点尽可能相似，簇间的数据点尽可能不同。

---

K-means 是一种常见的聚类算法，其流程如下：

1. 假如要将数据分成$K$个簇，首先生成 $K$个初始中心点 $\boldsymbol{\mu}_k$，每个中心点代表一个簇
2. 对于每一个数据点，分配到最近的中心点所代表的簇。若用$r_{i, k}\in\{0, 1\}$表示$\boldsymbol{x}_i$是否属于第$k$个簇，则有：

   $$r_{i, k}=\begin{cases} 1, & \text{if } k=\arg\min_j \Vert \boldsymbol{x}_i-\boldsymbol{\mu}_j\Vert^2\\ 0, & \text{otherwise} \end{cases}$$

3. 更新中心点，使得每个簇的中心点是簇内所有数据点的平均值：

   $$\boldsymbol{\mu}_k=\frac{\sum_{i=1}^N r_{i, k}\boldsymbol{x}_i}{\sum_{i=1}^N r_{i, k}}$$

---

接下来讨论 K-means 是否收敛。

可以定义如下目标函数：

$$J=\sum_{i=1}^N \sum_{k=1}^K r_{i, k}\Vert \boldsymbol{x}_i-\boldsymbol{\mu}_k\Vert^2$$

这个目标函数的含义是，每个数据点到其所属簇中心的距离之和。K-means 就相当于在最小化这个目标函数。易知，$J$是单调递减的，因为每次迭代都会使得$J$减小。所以 K-means 一定会收敛。

---

易知，随着$K$增大，$J$总是减小的。一般，可以用肘部法则来确定最佳的$K$值：

---

K-means 聚类的效果还与初始中心点高度相关。一般有以下几种初始化方法：

• 随机初始化。这种方法可能导致初始生成邻近的中心点，使得最终聚类效果不好
• 基于距离的初始化。第一个中心点随机生成，接下来选择离现存中心点最远的数据点作为下一个中心点。这种方法的问题是可能选择到一些离群点。
• 随机+基于距离的初始化。先随机生成一个中心点，然后基于距离选择下一个中心点，剩下的距离离目前的中心点越远，被选中的概率越大。

---

K-means 也有一些问题，例如对离群值敏感，难以处理非球形簇等。

有一种改进是软 K-means。$r_{i, k}$的含义变为$\boldsymbol{x}_i$属于第$k$个簇的概率：

$$r_{i, k}=\frac{\exp(-\Vert \boldsymbol{x}_i-\boldsymbol{\mu}_k\Vert^2)}{\sum_{j=1}^K \exp(-\Vert \boldsymbol{x}_i-\boldsymbol{\mu}_j\Vert^2)}$$

中心点更新公式不变。

第十二讲 隐变量模型

Latent Variable Model。

1、引入

在第三讲中我们提到，分类和回归这种有监督学习都可以看成是在学习某个条件概率分布$p(y|\boldsymbol{x};\boldsymbol{w})$。无监督学习也可以看成是在学习某个概率分布$p(\boldsymbol{x};\boldsymbol{w})$。

由于没有标签$y$，对$\boldsymbol{x}$建模要困难许多。一种最简单的想法是将$\boldsymbol{x}$的分布限定为某个高斯分布$\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})$，显然这种模型的表达能力很有限。

---

设想引入一个简单的分类分布$p(\boldsymbol{z})$，满足$p(\boldsymbol{z}_i)=\boldsymbol{\pi}_i, i=1, 2, \cdots, K$。我们将其与一个高斯分布组合起来：

$$p(\boldsymbol{x})=\sum_{i=1}^K p(\boldsymbol{x}|\boldsymbol{z}_i)p(\boldsymbol{z}_i)=\sum_{i=1}^K \boldsymbol{\pi}_i\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)$$

则我们可以获得一个更复杂的分布：

---

这里的$p(\boldsymbol{z})$可以代表数据隐藏的结构。一般地，隐变量模型是带有隐变量的概率模型：

$$p(\boldsymbol{x}, \boldsymbol{z})$$

其中$\boldsymbol{z}$就称为隐变量。隐变量也可以有多个，如$p(\boldsymbol{x}, \boldsymbol{z}_1, \boldsymbol{z}_2, \cdots, \boldsymbol{z}_K)$。

相应的，关于$\boldsymbol{x}$的概率$p(\boldsymbol{x})$是一个边缘概率，可以写为：

$$p(\boldsymbol{x})=\int_{\boldsymbol{z}} p(\boldsymbol{x}, \boldsymbol{z})d\boldsymbol{z}$$

2、高斯隐变量模型

若隐变量的分布是一个高斯分布：

$$p(\boldsymbol{z})=\mathcal{N}(\boldsymbol{z}|\boldsymbol{0}, \boldsymbol{I})$$

引入参数$\boldsymbol{W}$写出条件概率$p(\boldsymbol{x}|\boldsymbol{z})$，假定其也是一个高斯分布：

$$p(\boldsymbol{x}|\boldsymbol{z})=\mathcal{N}(\boldsymbol{x}|\boldsymbol{W}\boldsymbol{z}+\boldsymbol{\mu}, \sigma^2 \boldsymbol{I})$$

我们可以通过最大化其（对数）似然概率：

$$\log p(\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_N)= \log \prod_{i=1}^N p(\boldsymbol{x}_i)=\sum_{i=1}^N \log p(\boldsymbol{x}_i)$$

来得到能最好拟合真实数据的参数。

---

由$p(\boldsymbol{x}|\boldsymbol{z})$的表达式，可知

$$\boldsymbol{x}=\boldsymbol{\mu}+\boldsymbol{Wz}+\boldsymbol{\epsilon}$$

其中$\boldsymbol{\epsilon}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2 \boldsymbol{I})$。因为高斯分布的线性组合仍然是高斯分布，所以$\boldsymbol{x}$也是服从高斯分布的。这个多维高斯分布的期望为：

$$E[\boldsymbol{x}]=\boldsymbol{\mu}+\boldsymbol{W}\mathbb{E}[\boldsymbol{z}]+\mathbb{E}[\boldsymbol{\epsilon}]=\boldsymbol{\mu}$$

协方差为：

$$\text{Cov}[\boldsymbol{x}]=\mathbb{E}[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^T]=\boldsymbol{W}\boldsymbol{W}^T+\sigma^2 \boldsymbol{I}$$

所以有：

$$p(\boldsymbol{x})=\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}, \boldsymbol{W}\boldsymbol{W}^T+\sigma^2 \boldsymbol{I})$$

---

回头看我们对数似然概率，可以写成：

$$\begin{split} \sum_{i=1}^N \log \mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}, \boldsymbol{W}\boldsymbol{W}^T+\sigma^2 \boldsymbol{I})=-\frac 1 2\left[ND\log{2\pi}+N\log \vert \boldsymbol{W}\boldsymbol{W}^T+\sigma^2 \boldsymbol{I}\vert\right]-\\ \frac 1 2\sum_{i=1}^N(\boldsymbol{x}_i-\boldsymbol{\mu})^T(\boldsymbol{W}\boldsymbol{W}^T+\sigma^2 \boldsymbol{I})^{-1}(\boldsymbol{x}_i-\boldsymbol{\mu}) \end{split}$$

记$\boldsymbol{\Sigma}=\boldsymbol{W}\boldsymbol{W}^T+\sigma^2 \boldsymbol{I}, \boldsymbol{S}=\sum_{i=1}^N(\boldsymbol{x}_i-\boldsymbol{\mu})(\boldsymbol{x}_i-\boldsymbol{\mu})^T$，则：

$$\frac{\partial\log p(\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_N)}{\partial \boldsymbol{\mu}}=0 \Rightarrow \boldsymbol{\mu}=\frac 1 N \sum_{i=1}^N \boldsymbol{x}_i$$

$$\frac{\partial\log p(\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_N)}{\partial \boldsymbol{\Sigma}}=-\frac N 2 (\boldsymbol{\Sigma}^{-1}-\boldsymbol{\Sigma}^{-1}\boldsymbol{S}\boldsymbol{\Sigma}^{-1})=0 \Rightarrow \boldsymbol{\Sigma}=\boldsymbol{S}$$

综上，在最大化似然概率时，易知$\boldsymbol{x} \sim \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma})=\mathcal{N}(\overline{\boldsymbol{x}}, \boldsymbol{S})$。

---

进一步可求出$\boldsymbol{W}=\boldsymbol{U}\sqrt{\Lambda-\sigma^2 \boldsymbol{I}}$，其中

• $\boldsymbol{U}$由$\boldsymbol{S}$的前$M$个特征向量组成
• $\Lambda$是$\boldsymbol{S}$的前$M$个特征值组成的对角矩阵

所以$\boldsymbol{W}$就可以视作没有经过正则化的数据$\boldsymbol{x}$的主成分，其中每$i$个成分被放大了$\sqrt{\lambda_i-\sigma^2}$倍。

所以高斯隐变量模型也被称为概率 PCA。

3、高斯混合模型

Gaussian Mixture Model，GMM。

在高斯混合模型中，我们假设数据是由多个高斯分布混合而成的：

$$p(\boldsymbol{x})=\sum_{i=1}^K \pi_i\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)$$

其中$\pi_i$是权重，满足$\sum_{i=1}^K \pi_i=1$。

---

高斯混合模型可以写作隐变量模型的形式。引入隐变量$\boldsymbol{z}$，且$\boldsymbol{z}$是一个独热编码，记$\boldsymbol{z}_i$表示第$i$个元素为 1，其他元素为 0 的向量。

隐变量的分布写为$p(\boldsymbol{z})$，满足$p(\boldsymbol{z}_i)=\pi_i$。条件概率$p(\boldsymbol{x}|\boldsymbol{z})$写为$p(\boldsymbol{x}|\boldsymbol{z}_i)=\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)$。这就得到了高斯混合模型的隐变量模型形式。

通过最大化似然概率，可以得到最优参数$\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i, \pi_i$。

有了$\boldsymbol{x}$的分布之后，可以计算后验概率：

$$p(\boldsymbol{z}_i|\boldsymbol{x})=\frac{p(\boldsymbol{x}|\boldsymbol{z}_i)p(\boldsymbol{z}_i)}{p(\boldsymbol{x})}=\frac{\pi_i\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)}{\sum_{j=1}^K \pi_j\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}$$

这个后验概率的含义就是，数据点$\boldsymbol{x}$属于第$i$个高斯分布的概率，相当于在做聚类。

---

LVM 还运用在隐式马尔科夫模型、Sigmoid 信念网络（SBN）、隐式狄利克雷分布（LDA）等模型中。

第十三讲 EM 算法

Expectation Maximization Algorithm，期望最大化算法。

EM 算法是用于解决下面的问题：假如有联合分布$p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})$，我们需要最大化对数似然概率（一个边缘概率）$p(\boldsymbol{x}; \boldsymbol{\theta})$，也即：

$$\boldsymbol{\theta}^*=\arg\max_{\boldsymbol{\theta}} \log p(\boldsymbol{x}; \boldsymbol{\theta})$$

---

EM 算法是一种迭代算法，每次迭代分两步：

1. E-step：计算下面这个期望：

   $$Q(\boldsymbol{\theta};\boldsymbol{\theta}^{(t)})=\mathbb{E}_{\boldsymbol{z}\sim p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)})}[\log p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})]$$

   这实际上是在给定数据$\boldsymbol{x}$和参数$\boldsymbol{\theta}^{(t)}$的情况下，先算出隐变量$\boldsymbol{z}$的分布（一个后验分布），然后计算联合概率在这个分布上的期望。
2. M-step：更新参数使这个期望最大化：

   $$\boldsymbol{\theta}^{(t+1)}=\arg\max_{\boldsymbol{\theta}} Q(\boldsymbol{\theta};\boldsymbol{\theta}^{(t)})$$

1、理论推导

将对数似然概率重写。假定$q(\boldsymbol{z})$是任意的分布，由$\sum_{\boldsymbol{z}} q(\boldsymbol{z})=1$有：

$$\begin{align*} \log p(\boldsymbol{x}; \boldsymbol{\theta})&=\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log p(\boldsymbol{x}; \boldsymbol{\theta})=\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log \frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}\\ &=\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log \frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z})}+\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log \frac{q(\boldsymbol{z})}{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}\\ &=\mathcal{L}(q, \boldsymbol{\theta})+\text{KL}(q\Vert p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})) \end{align*}$$

前一项我们称之为变分下界，它是对数似然概率的一个下界。通过最大化这个下界可以间接最大化对数似然概率。

后一项我们称之为KL 散度，它用于衡量两个分布的相似程度。实际上我们这里就是在用任意一个分布$q(\boldsymbol{z})$来拟合真正的后验分布 $p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})$。

---

KL 散度一般的定义为：

$$\text{KL}(q\Vert p)=\int q(\boldsymbol{z})\log \frac{q(\boldsymbol{z})}{p(\boldsymbol{z})} d\boldsymbol{z}\geqslant 0$$

下面这张图可以直观地解释 KL 散度：

---

若取$q(\boldsymbol{z})=p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)})$，则参数为$\boldsymbol{\theta}^{(t)}$时的对数似然概率为：

$$\log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t)})=\mathcal{L}(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)}), \boldsymbol{\theta}^{(t)})=\sum_{\boldsymbol{z}} p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)})\log \frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta}^{(t)})}{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)})}$$

KL 散度恰好为 0，直接舍去。如果我们更新参数：

$$\boldsymbol{\theta}^{(t+1)}=\arg\max_{\boldsymbol{\theta}} \mathcal{L}(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)}), \boldsymbol{\theta})$$

则一定有：

$$\mathcal{L}(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)}), \boldsymbol{\theta}^{(t+1)})\geqslant \mathcal{L}(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)}), \boldsymbol{\theta}^{(t)})=\log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t)})$$

我们再看参数为$\boldsymbol{\theta}^{(t+1)}$时的对数似然概率：

$$\log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t+1)})=\mathcal{L}(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)}), \boldsymbol{\theta}^{(t+1)})+\text{KL}(p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t)})\Vert p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta}^{(t+1)}))\geqslant \log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t)}) +0$$

所以按照上面更新参数的方法，总有：

$$\log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t+1)})\geqslant \log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t)})$$

---

接下来，只需证明 EM 算法和上述过程等价。因为：

$$\mathcal{L}(q, \boldsymbol{\theta})=\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log \frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z})}=\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})-\sum_{\boldsymbol{z}} q(\boldsymbol{z})\log q(\boldsymbol{z})$$

后半部分其实就是$q(\boldsymbol{z})$的熵，可以忽略。而前半部分正是 E-step 中的期望。所以 EM 算法和上述过程等价。

2、训练 GMM

GMM 可以利用 EM 算法来训练。

首先是 E-step。由于：

$$p(\boldsymbol{z}_j|\boldsymbol{x}_i; \boldsymbol{\theta}^{(t)})=\frac{\mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}^{(t)}_j, \boldsymbol{\Sigma}^{(t)}_j)\pi^{(t)}_j}{\sum_{k=1}^K \mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}^{(t)}_k, \boldsymbol{\Sigma}^{(t)}_k)\pi^{(t)}_k}=\gamma^{(t)}_{i, j}$$

所以：

$$\log p(\boldsymbol{x}_i, \boldsymbol{z}; \boldsymbol{\theta}^{(t)})=\sum_{j=1}^K [\log \mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}^{(t)}_j, \boldsymbol{\Sigma}^{(t)}_j)+\log \pi^{(t)}_j]$$

所以对于单个数据点$\boldsymbol{x}_i$，期望为：

$$Q(\boldsymbol{\theta}; \boldsymbol{\theta}^{(t)})=\sum_{j=1}^K \gamma_{i, j}^{(t)}[\log \mathcal{N}(\boldsymbol{x}_i|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)+\log \pi_j]$$

将高斯分布也展开：

$$Q(\boldsymbol{\theta}; \boldsymbol{\theta}^{(t)})=\sum_{j=1}^K \gamma_{i, j}^{(t)}\left[-\frac 1 2 \log \vert \boldsymbol{\Sigma}_j\vert-\frac 1 2 (\boldsymbol{x}_i-\boldsymbol{\mu}_j)^T\boldsymbol{\Sigma}_j^{-1}(\boldsymbol{x}_i-\boldsymbol{\mu}_j)+\log \pi_j\right]$$

考虑所有数据，平均期望就是：

$$Q(\boldsymbol{\theta}; \boldsymbol{\theta}^{(t)})=\frac 1 N\sum_{i=1}^N \sum_{j=1}^K \gamma_{i, j}^{(t)}\left[-\frac 1 2 \log \vert \boldsymbol{\Sigma}_j\vert-\frac 1 2 (\boldsymbol{x}_i-\boldsymbol{\mu}_j)^T\boldsymbol{\Sigma}_j^{-1}(\boldsymbol{x}_i-\boldsymbol{\mu}_j)+\log \pi_j\right]+C$$

---

接下来是 M-step。上面已经求出了期望的式子，分别对$\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j$求偏导并令其为 0，可以得到：

$$\begin{align*} &\boldsymbol{\mu}_j^{(t+1)}=\frac{1}{N_j} \sum_{i=1}^N \gamma_{i, j}^{(t)}\boldsymbol{x}_i\\ &\boldsymbol{\Sigma}_j^{(t+1)}=\frac{1}{N_j} \sum_{i=1}^N \gamma_{i, j}^{(t)}(\boldsymbol{x}_i-\boldsymbol{\mu}_j^{(t+1)})(\boldsymbol{x}_i-\boldsymbol{\mu}_j^{(t+1)})^T \end{align*}$$

其中$N_j=\sum_{i=1}^N \gamma_{i, j}^{(t)}$，可以理解为所有数据点分到第$j$类的概率之和。对于$\pi_j$，在约束$\sum_{j=1}^K \pi_j=1$下，可以求出解：

$$\pi_j^{(t+1)}=\frac{N_j}{N}$$

---

总结一下，如果第$t$轮的参数为$\boldsymbol{\mu}^{(t)}, \boldsymbol{\Sigma}^{(t)}, \pi^{(t)}$，首先利用其计算$\gamma_{i, j}^{(t)}$，然后根据上面的公式更新参数$\boldsymbol{\mu}^{(t+1)}, \boldsymbol{\Sigma}^{(t+1)}, \pi^{(t+1)}$。重复这个过程直到收敛。

---

如果将$\boldsymbol{\Sigma}_k$限定为对角矩阵$\sigma^2 I$的形式，且固定$\pi_k=\frac 1 K$，则 GMM 就退化为$\beta=\frac {1}{2\sigma^2}$的软 K-means。

3、EM 变体

上面我们讨论了 EM 在训练 GMM 中的应用，实际问题中的后验分布不总是高斯分布，期望和参数更新都不一定有闭式解。

3.1、EM+SGD

推导 EM 算法的过程中，我们发现最大化期望，只是在保证似然概率不减。事实上，保证似然概率不减，不一定要最大化期望。

对期望利用梯度上升法来更新参数：

$$\boldsymbol{\theta}^{(t+1)}=\boldsymbol{\theta}^{(t)}+\eta \nabla_{\boldsymbol{\theta}} Q(\boldsymbol{\theta}; \boldsymbol{\theta}^{(t)})$$

显然有：

$$Q(\boldsymbol{\theta}^{(t+1)}; \boldsymbol{\theta}^{(t)})\geqslant Q(\boldsymbol{\theta}^{(t)}; \boldsymbol{\theta}^{(t)})$$

由于$p(\boldsymbol{z})$的熵可以认为是不变的，所以根据 EM 算法的推导过程可以反向推导出，仍然有：

$$\log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t+1)})\geqslant \log p(\boldsymbol{x}; \boldsymbol{\theta}^{(t)})$$

3.2、MCMC EM

Markov Chain Monte Carlo EM。

其中 MCMC 是一种采样方法，由于我们并不总是知道后验分布的形式，所以可以通过 MCMC 来近似采样。

所以期望可以用这些采样值来近似：

$$Q(\boldsymbol{\theta}; \boldsymbol{\theta}^{(t)})\approx \frac 1 S \sum_{s=1}^S \log p(\boldsymbol{x}, \boldsymbol{z}_s; \boldsymbol{\theta})$$

再结合 SGD，就得到了 MCMC EM，这是常用于训练隐变量模型的方法。

3.3、VB EM

Variational Bayes EM，变分贝叶斯 EM。

直接在高维空间中采样出$\boldsymbol{z}_s$代价比较大。VB EM 的基本思想是用一个简单的分布$q(\boldsymbol{z}; \boldsymbol{\phi})$来近似$p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})$，然后在这个简单的分布上进行 EM 算法。

这个简单的分布，可以是每个维度用一个高斯分布的组合：

$$z_i\sim \mathcal{N}(\mu_i, \sigma_i^2)$$

然后找到能最小化与原后验分布 KL 散度的参数$\boldsymbol{\phi}$。

---

将最小化 KL 散度进行转化：

$$\min_{\boldsymbol{\phi}} \text{KL}(q(\boldsymbol{z}; \boldsymbol{\phi})\Vert p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})) \Leftrightarrow \max_{\boldsymbol{\phi}} \int q(\boldsymbol{z}; \boldsymbol{\phi})\log \frac{p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})}{q(\boldsymbol{z}; \boldsymbol{\phi})}d\boldsymbol{z} \Leftrightarrow \max_{\boldsymbol{\phi}} \int q(\boldsymbol{z}; \boldsymbol{\phi})\log \frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{p(\boldsymbol{z}; \boldsymbol{\phi})}d\boldsymbol{z}$$

中间，我们舍去了$\log p(\boldsymbol{x}; \boldsymbol{\theta})$，因为它与$\boldsymbol{\phi}$无关。

后续利用这个近似分布最大化梯度可以写为：

$$\max_{\boldsymbol{\theta}} \mathbb{E}_{q(\boldsymbol{z}; \boldsymbol{\phi})}[\log p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})]= \max_{\boldsymbol{\theta}} \int q(\boldsymbol{z}; \boldsymbol{\phi})\log p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})d\boldsymbol{z}\Leftrightarrow \max_{\boldsymbol{\theta}} \int q(\boldsymbol{z}; \boldsymbol{\phi})\log\frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}; \boldsymbol{\phi})}d\boldsymbol{z}$$

这里添加了与$\boldsymbol{\theta}$无关的项$\log p(\boldsymbol{x}; \boldsymbol{\theta})$，不影响最大化。

可以发现最小化散度和最大化期望可以转化为相同的形式。所以以上两个问题统一写为：

$$\max_{\boldsymbol{\theta}, \boldsymbol{\phi}} \int q(\boldsymbol{z}; \boldsymbol{\phi})\log\frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}; \boldsymbol{\phi})}d\boldsymbol{z}=\max_{\boldsymbol{\theta}, \boldsymbol{\phi}} \int \mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})d\boldsymbol{z}$$

利用梯度下降法，同时更新$\boldsymbol{\theta}, \boldsymbol{\phi}$，这就是 VB EM。

---

可以证明，$\mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})$是任意参数的对数似然概率的下界。VB EM 在最大化这个下界，也就是在最大化对数似然概率。

第十四讲 深度生成模型

数据的生成过程可以用一个联合概率分布函数来描述：

$$p(\boldsymbol{x}, \boldsymbol{z})=p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})$$

也即由隐变量$\boldsymbol{z}$生成数据$\boldsymbol{x}$。显然，这也可以看成是一个隐变量模型。这就是普通的生成模型（GM）。

之前介绍的 PCA 是隐变量模型：

$$\begin{align*} &p(\boldsymbol{z})=\mathcal{N}(\boldsymbol{z}|\boldsymbol{0}, \boldsymbol{I})\\ &p(\boldsymbol{x}|\boldsymbol{z})=\mathcal{N}(\boldsymbol{x}|\boldsymbol{W}\boldsymbol{z}+\boldsymbol{\mu}, \sigma^2 \boldsymbol{I}) \end{align*}$$

GMM 也是隐变量模型：

$$\begin{align*} &p(\boldsymbol{z}_i)=\pi_i\\ &p(\boldsymbol{x}|\boldsymbol{z}_i)=\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i) \end{align*}$$

---

为了增强模型的表达能力，我们在$p(\boldsymbol{z})$和$p(\boldsymbol{x}|\boldsymbol{z})$中引入深度神经网络，于是联合概率分布可以写为：

$$p(\boldsymbol{x}, \boldsymbol{z})=p(\boldsymbol{x}|T(\boldsymbol{z}))p(\boldsymbol{z})$$

其中$T(\cdot)$就代表一个神经网络。这样，我们就得到了深度生成模型（DGM）。

---

例如在生成图片的时候，DGM 可以具体的写为：

$$p(\boldsymbol{x}, \boldsymbol{z})=\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}(\boldsymbol{z}), \boldsymbol{I})\mathcal{N}(\boldsymbol{z}|\boldsymbol{0}, \boldsymbol{I})$$

其中$\boldsymbol{\mu}(\boldsymbol{z})$就是一个神经网络。如过神经网络的结构如下图：

则有：

$$\boldsymbol{\mu}(\boldsymbol{z})=\boldsymbol{W}_3a(\boldsymbol{W}_2a(\boldsymbol{W}_1\boldsymbol{z}+\boldsymbol{b}_1)+\boldsymbol{b}_2)+\boldsymbol{b}_3$$

在 PCA 中，则有：

$$\boldsymbol{\mu}(\boldsymbol{z})=\boldsymbol{W}\boldsymbol{z}+\boldsymbol{b}$$

后续，将神经网络涉及的参数简记一个符号$\boldsymbol{\theta}$，$\boldsymbol{\mu}(\boldsymbol{z})$就可以写为$\boldsymbol{\mu}(\boldsymbol{z}; \boldsymbol{\theta})$。

1、VB EM 训练 DGM

我们知道 VB EM 的基本思想是用一个简单的分布$q(\boldsymbol{z}; \boldsymbol{\phi})$来近似$p(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\theta})$，然后在这个简单的分布上进行 EM 算法。

优化这个近似的分布和 E-step 中的期望可以统一的写为最大化下面这个式子：

$$\mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})=\int q(\boldsymbol{z}; \boldsymbol{\phi})\log\frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}; \boldsymbol{\phi})}d\boldsymbol{z}$$

进一步，由$p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})=p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})p(\boldsymbol{z})$，所以：

$$\begin{align*} \mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})&=\int q(\boldsymbol{z}; \boldsymbol{\phi})\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})d\boldsymbol{z}-\int q(\boldsymbol{z}; \boldsymbol{\phi})\log \frac{q(\boldsymbol{z}; \boldsymbol{\phi})}{p(\boldsymbol{z})}d\boldsymbol{z}\\ &=\mathbb{E}_{q(\boldsymbol{z}; \boldsymbol{\phi})}[\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})]-\text{KL}(q(\boldsymbol{z}; \boldsymbol{\phi})\Vert p(\boldsymbol{z})) \end{align*}$$

---

接下来，考虑一个具体的例子：$p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})=\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}(\boldsymbol{z}; \boldsymbol{\theta}), \boldsymbol{I})$，$q(\boldsymbol{z}; \boldsymbol{\phi})=\mathcal{N}(\boldsymbol{z}|\boldsymbol{\lambda}, \text{diag}(\boldsymbol{\eta}^2))$

也即$p(\boldsymbol{x}|\boldsymbol{z})$和$q(\boldsymbol{z})$都是高斯分布，且协方差矩阵是对角矩阵。$\boldsymbol{\phi}$包括参数$\boldsymbol{\lambda}, \boldsymbol{\eta}$。

要最大化$\mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})$，考虑使以下两个偏导为 0：

$$\frac{\partial \mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})}{\partial \boldsymbol{\theta}}=0, \frac{\partial \mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})}{\partial \boldsymbol{\phi}}=0$$

对于$\mathcal{L}(\boldsymbol{x};\boldsymbol{\theta}, \boldsymbol{\phi})$中散度的部分，由于$\boldsymbol{q}(z; \boldsymbol{\phi})$和$p(\boldsymbol{z})$都是高斯分布，所以 这部分偏导为 0 有闭公式解。

但是对于期望的部分，由于$\boldsymbol{\mu}(\boldsymbol{z}; \boldsymbol{\theta})$是一个神经网络，所以这部分的偏导没有闭式解。

2、重参数化技巧

在 MCMC EM 中提到，可以利用采样的方法来近似期望。在 DGM 中，我们同样可以这样做。但是，如果直接对$q(\boldsymbol{z}; \boldsymbol{\phi})$采样，这样采样出的只是单纯的数据点，并不包含对应的参数$\boldsymbol{\lambda}, \boldsymbol{\eta}$。

所以，我们可以利用重参数化技巧。先从一个标准正态分布$\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$中采样出一个$\boldsymbol{\epsilon}$，然后做一个映射：

$$\boldsymbol{z}=\boldsymbol{\lambda}+\boldsymbol{\eta}\odot\boldsymbol{\epsilon}$$

有$\boldsymbol{z}\sim \mathcal{N}(\boldsymbol{\lambda}, \text{diag}(\boldsymbol{\eta}^2))$。所以$\boldsymbol{z}$就相当于从$q(\boldsymbol{z}; \boldsymbol{\phi})$中采样出来的数据点，且显示带有参数$\boldsymbol{\lambda}, \boldsymbol{\eta}$。

---

由于$p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})$的协方差矩阵是对角矩阵，所以：

$$\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})=C-\frac 1 2 \Vert \boldsymbol{x}-\boldsymbol{\mu}(\boldsymbol{z}; \boldsymbol{\theta})\Vert^2=C-\frac 1 2 \Vert \boldsymbol{x}-\boldsymbol{\mu}(\boldsymbol{\lambda}+\boldsymbol{\eta}\odot\boldsymbol{\epsilon}; \boldsymbol{\theta})\Vert^2$$

于是，期望可以用采样数据来估计：

$$\mathbb{E}_{q(\boldsymbol{z}; \boldsymbol{\phi})}[\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})]\approx \frac 1 S \sum_{s=1}^S [C-\frac 1 2 \Vert \boldsymbol{x}-\boldsymbol{\mu}(\boldsymbol{\lambda}+\boldsymbol{\eta}\odot\boldsymbol{\epsilon}_s; \boldsymbol{\theta})\Vert^2]=\tilde L(\boldsymbol{x}; \boldsymbol{\theta}, \boldsymbol{\phi})$$

这种形式下，期望对参数$\boldsymbol{\theta}$以及$\boldsymbol{\phi}$的偏导是可求的了。利用自动微分+反向传播，就能对这个期望的近似值进行优化。

3、在整个数据集上的训练

为了优化最终的目标，对于数据集上的每个数据点$\boldsymbol{x}_i$，最好都要有一个对应的$q_i(\boldsymbol{z}; \boldsymbol{\phi}_i)$，也即有对应的参数$\boldsymbol{\phi}_i=\{\boldsymbol{\lambda}_i, \boldsymbol{\eta}_i\}$。

由于$\boldsymbol{\theta}$会在所有样本上更新，而$\boldsymbol{\phi}$是在单个样本上更新，所以后者的更新频率可能会更高。但是为了保证能够有一个较好的后验分布近似$q_i(\boldsymbol{z}; \boldsymbol{\phi}_i)$，我们需要提高$\boldsymbol{\phi}_i$的更新频率。

我们引入两个深度神经网络$g(\cdot;\boldsymbol{\phi}_1), g(\cdot;\boldsymbol{\phi}_2)$，让参数$\boldsymbol{\lambda}_i, \boldsymbol{\eta}_i$由这两个网络输出，也即：

$$\boldsymbol{\lambda}_i=g(\boldsymbol{x}_i;\boldsymbol{\phi}_1), \boldsymbol{\eta}_i=g(\boldsymbol{x}_i;\boldsymbol{\phi}_2)$$

所以只需要同时训练这两个网络就行，这两个网络就能给出所有数据点的$\boldsymbol{\lambda}_i, \boldsymbol{\eta}_i$。不仅更新频率提高了，且相比单独训练每组参数，训练网络的效率更高。

最终，整个 DGM 模型的目标函数如下：

网络$g(\cdot;\boldsymbol{\phi}_1)$可以看作是编码器。由于$\boldsymbol{\epsilon}$是从标准正态分布中采样的，可以将$g(\cdot;\boldsymbol{\phi}_2)\odot \boldsymbol{\epsilon}$看作是一个高斯噪声。

由$\boldsymbol{z}$到$\boldsymbol{x}$的网络$\boldsymbol{\mu}(\boldsymbol{z}; \boldsymbol{\theta})$可以看作是解码器。我们还加入了一个 KL 散度作为正则项。

---

以上，其实就是所谓的变分自编码器（VAE）：

相比普通的自编码器（AE），VAE 引入了一个正则项 KL 散度，同时还引入了高斯噪声。

第十五讲 表示学习

Representation Learning

1、引入

表示学习的目标是将数据点$x_i$映射到空间$\mathbb{R}^d$中的一个向量。显然，这种映射方式有无数种，我们希望找到这样一种映射，可以保留尽可能多的语义信息（Semantic Information）。这里的$x_i$不是标量的意思，可以代表各种类型的数据，例如图片、文本等。

例如，数据为手写数字的图片。我们希望映射后，相同数字的图片在空间中尽可能相近。

这样重新表示后，数据更为紧凑（Compact），而且仅保留了重要的语义信息，便于后续的处理，也很容易使用一些下游的方法来处理：例如分类、聚类等。

2、图片表示

对于有监督的情况，之前介绍过用 CNN 来训练一个分类器：

卷积-池化层的部分可以看成在做特征提取，全连接层的部分可以看成在做分类。则最后一个卷积-池化层的输出就可以看作是对原始图片的一个重新表示。有时，全连接层的输出也可以看作是一个表示。

---

对于无监督的情况，可以先用一个带标签的辅助数据集训练一个 CNN，这个预训练的 CNN 同样可以看为是特征提取。

再在无标签的数据集上，用这个预训练的 CNN，就得到了一个新的表示。

上一讲介绍到的变分自编码器，其中的编码器就相当于做特征提取，编码后的结果也可以看做是一个表示。PCA 可以看做是一个线性的自编码器。

2.1、SimCLR

Simple Framework for Contrastive Learning，是一种对比学习（Contrastive Learning）框架，

对于一张图片，我们可以对其做一些变换，例如裁剪、旋转、翻转等，这个过程也称为数据增广（Data Augmentation）：

$$\boldsymbol{x}_i^+=\text{aug}(\boldsymbol{x}_i)$$

---

SimCLR 的基本思想就是让$\boldsymbol{x}_i$和$\boldsymbol{x}_i^+$在表示空间中尽可能接近，而与其他图片$\boldsymbol{x}_j$及其增广$\boldsymbol{x}_j^+$更远：

图中$\boldsymbol{h}_i, \boldsymbol{h}_j$就可以看作是$\tilde{\boldsymbol{x}}_i, \tilde{\boldsymbol{x}}_j$的表示。$g(\cdot)$被称为投影头（Projection Head），通常是一个较浅的神经网络，类似于 CNN 分类器中最后的全连接层。

某个数据点上的损失函数（称之为InfoNCE Loss）可以写为：

$$L=-\log \frac{\exp(\text{sim}(\boldsymbol{z}_i, \boldsymbol{z}_i^+)/\tau)}{\sum_{j\neq i}\exp(\text{sim}(\boldsymbol{z}_i, \boldsymbol{z}_j)/\tau)+\sum_{j\neq i}\exp(\text{sim}(\boldsymbol{z}_i, \boldsymbol{z}_j^+)/\tau)+\exp(\text{sim}(\boldsymbol{z}_i, \boldsymbol{z} _j^+)/\tau)}$$

其中$\text{sim}(\boldsymbol{z}_i, \boldsymbol{z}_j)=\boldsymbol{z}_i^T\boldsymbol{z}_j/\Vert \boldsymbol{z}_i\Vert \Vert \boldsymbol{z}_j\Vert$

由这个函数可以看出，最小化这个损失，就是在尽可能将$\boldsymbol{z}_i$和$\boldsymbol{z}_i^+$拉近，同时将$\boldsymbol{z}_i$和其他图片的表示拉远。当在所有数据点上同时做这件事时，不仅每个点及其增广倾向于接近，相同类别的点也会更接近。举例来说的话，一张狗的图片及其变形会尽量接近，同时不同的狗的图片之间也会倾向于接近。

---

首先利用 SimCLR 在某个无标签的大数据集上训练一个特征提取器$f(\cdot)$，然后冻结特征提取器（不更新其中的参数），对比着少量带标签的数据训练一个线性分类器$g(\cdot)$，得到整个模型。

其中前半部分可以看作是在训练一个一般的特征提取器，后半部分可以看作针对任务进行的微调。

后半部分训练的投影头可以显著提升整个模型的性能：

同时使用大批量的数据进行训练也可以显著提升 SimCLR 的性能，但是也会对硬件有更高的要求：

---

对于两个服从联合分布$p(x, y)$的随机变量$X, Y$，它们的互信息（Mutual Information）定义为：

$$I(X, Y)=\int p(x, y)\log \frac{p(x, y)}{p(x)p(y)}dxdy$$

可以从不同的角度理解：

• $I(x, y)=\text{KL}(p(x, y)\Vert p(x)p(y))$：这两个分布之间的 KL 散度(“距离”)
• $I(x, y)=H(x)-H(x|y)=H(y)-H(y|x)$：已知一个变量给另一个变量带来的信息量

直观来说，互信息可以理解为两者之间的相关性，共享的信息量。

可以证明，互信息的一个下界是：

$$I(X, Y)\geqslant \log K+\mathbb{E}_{p(x, y)}\prod_{k=1}^K p(y_k)\log{\frac{e^{s(x, y)}}{e^{s(x, y)}+\sum_{k=1}^{K-1} e^{s(x, y_k)}}}$$

其中$p(y)=\int p(x, y)dx$是边缘分布。$s(x, y)$是一个任意形式的分布，实际中通过训练它，使得下界最大（更接近互信息）。

期望可以通过采样的方式估计。从联合分布中抽取一个样本$(x, y)$，然后从边缘分布中独立抽取$K-1$个样本$y_k$，就可以得到上面不等式右侧的一个下界的估计。于是一个下界的估计可以写为：

$$I(X, Y)\geqslant L\approx \log K+\log \frac{e^{s(x, y)}}{e^{s(x, y)}+\sum_{k=1}^{K-1} e^{s(x, y_k)}}$$

---

结合 SimCLR，两个随机变量$Z=g(f(\mathcal{T}(\boldsymbol{x})), Z^+=g(f(\mathcal{T}(\boldsymbol{x})))$，其中$\mathcal{T}(\cdot)$是随机的一个数据增广操作

所以可以写出这两个随机变量的互信息下界估计：

$$I(Z, Z^+)\geqslant \log N+\log \frac{e^{s(z, z^+)}}{e^{s(z, z^+)}+\sum_{k=1}^{N-1} e^{s(z, z_k^+)}}$$

由于分布$p(z)$和$p(z^+)$是相同的，所以对于$(z_i, z_i^+)$样本，视为从$p(z, z^+)$中采样；$(z_i, z_j^+)$样本，视为从$p(z^+)$中采样两次然后组合。

于是，这个下界的估计可以重新写为：

$$I(Z, Z^+)\geqslant \log (2N-1)+\log \frac{e^{s(z_i, z_i^+)}}{e^{s(z, z^+)}+\sum_{j\neq i} e^{s(z, z_j)}+\sum_{j\neq i} e^{s(z, z_j^+)}}$$

可以发现后半部分就是 InfoNCE 的负值。所以 SimCLR 目标是最小化 InfoNCE，可以理解为最大化互信息的下界，也即最大化互信息。直观上来讲，尽可能找到数据之间的关联。

2.2、MoCo

名字来源于 Momentum Contrast，是另一种对比学习框架。

---

首先引入一些概念。在 SimCLR 中，对原始数据$\boldsymbol{x}$做增广得到$\boldsymbol{x}^+$，我们分别称为锚点/基准点（Anchor）和正样本。相应的，其他的数据和它们的增广称为负样本。SimCLR 就是在训练一个编码器，使得由锚点和正样本编码出来的特征在表示空间中尽可能接近，而与负样本尽可能远。

对比学习可以看成是一个字典查询任务。构建一个字典，字典的键就是各个样本，值就是编码后的特征（表示）。我们称锚点的编码为 query（或者简记为 q，对应的原始数据为$\boldsymbol{x}^q$），正样本和负样本的编码为 key（或者简记为 k，对应的原始数据为$\boldsymbol{x}^k$）。对于一个 query，我们希望在字典中找到与之最接近的 key。注意，这里的 key 并不是（字典的）键的意思，只是一个称呼，其实际对应是字典的值。

---

SimCLR 中，实际是对锚点$\boldsymbol{x}^q$和正负样本$\boldsymbol{x}^k$使用相同的编码器得到 q 和 k，然后计算相似度，使得 q 和正样本的 k 的相似度尽可能大，而 q 和负样本的 k 相似度尽可能小，以此更新编码器参数。SimCLR 中，每个批次数据以及编码出的特征构成字典。所以字典大小与批次大小相关联，容易受到硬件瓶颈限制。

后来引入了 Memory Bank 的概念，所有样本的编码特征都存储在 Memory Bank 中。每次训练，正常获得 q，然后从 Memory Bank 中随机抽取部分 k 以及对应的$\boldsymbol{x}^k$构成字典，然后计算相似度，更新编码器参数。最后用新的编码器对$\boldsymbol{x}^k$ 重新编码，更新 Memory Bank。这种方法下，字典大小与批次大小解耦了，一定程度上解决了硬件瓶颈问题。

但是这种方法下，由于每次只更新 Memory Bank 的部分编码，所以会导致 Memory Bank 中的编码特征的一致性很差（不是同一个编码器编码的），最终导致 q 和 k 的相似度计算不准确。

---

MoCo 在 Memory Bank 的基础上进一步改进，它给 Memory Bank 引入了一个更新缓慢的动量编码器。动量编码器的参数更新不如主编码器那么频繁，所以 Memory Bank 中的编码特征相对比较一致。

另外，Memory Bank 换用队列结构。队列中的每个元素都是一个字典。对一个批次训练，使用队头的字典。主编码器、动量编码器的参数更新后，对使用到的字典用动量编码器进行更新，然后将这个字典放入队列的尾部，同时将队列头部的字典移除。

通过以上改进，不仅实现了字典大小与批次大小的解耦，还解决了 Memory Bank 中编码特征的一致性问题。

---

MoCo v2 结合了 SimCLR 中非线性投影头，以及 MoCo 中的 Memory Bank 和动量编码器，进一步提升了性能。

3、文本表示

3.1、独热编码、BOW 和 TFIDF

最简单的表示文本数据的方法，是将词表中的每一个词都用一个独热向量来表示。但显然，当句子非常长时，这种方法就非常的笨重。

---

另一种表示方法——词袋模型（Bag of Words，BOW），丢弃了句子内词的顺序信息，只考虑文本中每个词的数量，也即每个词被认为有同等的重要性。但是，不同的词所含的信息量是不同的（例如介词和名词，两者所含的信息相差甚远），所以这种方法也有局限性。

---

TFIDF，Term Frequency-Inverse Document Frequency，这种方法认为每个词有不同的重要性。

一个词的 TFIDF 计算公式为：

$$\text{TFIDF}(w, d, \mathcal{D})=\text{TF}(w, d)\cdot \text{IDF}(w, \mathcal{D})$$

其中$w$代表一个词，$d$代表第$d$篇文章，$\mathcal{D}$代表整个语料库。

$\text{TF}(w, d)$，也即名字中的的 TF ——词频，表示文章$d$中，$w$出现的频率$\text{TF}{(w, d)}=n_w/n$

$\text{IDF}(w, \mathcal{D})$，也即名字中的 IDF——文档频率倒数，实际表示出现$w$的文章的频率倒数的对数$\text{IDF}(w, \mathcal{D})=\log (N/N_{\text{contain w}})$。IDF 衡量了$w$包含信息的多少。$w$的 IDF 越大，说明其包含了越多信息，在语料的重要性更大。

---

以上三种方法均不能反映“近义词关系”，或者说语义相似性（Semantic Similarities），例如“soccer”和“football”在表示空间中可能很不一样。

而且用这三种方法进行表示，维度都比较高（尤其是独热编码），而且比较稀疏。BOW 和 TDIDF 还不包含词的顺序信息，而众所周知，同一个词在不同上下文的含义可能是完全相反的。

3.2、Word2Vex

基于上面三种方法的局限，我们希望设计出这样的一种文本表示方法：

• 表示是比较紧的（表示空间尽可能低维）
• 能够反映近义词（词之间的语义相似性）

一个朴素的观察是，如果两个词经常在句子中同时出现（或相互替换），就说明它们有某种程度的语义相似性，也就是说词的语义相似性隐含在句子中。我们可以通过学习大量的句子，来捕捉到这种相似性。

---

有两种基本的方法，Skip-grams 和 CBOW（Continuous Bag-of-Words）。前者是根据一个中心词来预测出前后的词，然后与原文比较，进行训练；后者是根据前后词预测出中心词，然后与原文比较，进行训练。

首先介绍 Skip-grams。一开始，每一个词都用一个随机的实值向量来表示$\boldsymbol{w}\in\mathbb{R}^m$，也称为这个词的（在表示空间中的）嵌入（Embedding）。

句子$\boldsymbol{w}_1\boldsymbol{w}_1\boldsymbol{w}_2\cdots \boldsymbol{w}_T$，遍历每个词作为中心词为$\boldsymbol{w}_t$，则目标是最小化下面这个函数：

$$J(\boldsymbol{\theta})=-\frac 1 T \sum_{t=1}^T \sum_{|j|\leqslant m,j\neq 0} \log P(\boldsymbol{w}_{t+j}|\boldsymbol{w}_t;\boldsymbol{\theta})$$

其中预测词出现的概率$P(\boldsymbol{w}_{t+j}|\boldsymbol{w}_t;\boldsymbol{\theta})$：

$$P(\boldsymbol{w}_{t+j}|\boldsymbol{w}_t;\boldsymbol{\theta})=\frac{\exp(\boldsymbol{w}_t^T \boldsymbol{w}_{t+j})}{\sum_{\boldsymbol{w}\in \mathcal{W}}\exp(\boldsymbol{w}_t^T \boldsymbol{w} )}$$

其中$\mathcal{W}$代表整个词典。

用大量语料训练后，具有语义相似性越大的两个词的嵌入（两个向量），其$\text{sim}(\boldsymbol{w}_i, \boldsymbol{w}_j)=\cos \theta$大。

CBOW 则反之，是类似的，这里不再赘述。

---

句子的嵌入可以通过句子中的词嵌入的平均得到$\mathbb{R}^m$，或者拼接为一个矩阵$\mathbb{R}^{T\times m}$，或者用 CNN/LSTM 进行提取（用下游任务训练句嵌入）。

3.3、ELMo

Word2Vex 一个缺点是，每个词都只有一个固定的嵌入。但是一个词可能有很多意思，不同的语义下应该用不同的嵌入方式。

因此，考虑根据输入的句子作为上下文，来具体计算每个词的表征，提出了 ELMo（Embeddings from Language Model）。其基本思想，是用训练语言模型的套路，把语言模型中间隐含层的输出提取出来，作为这个词在当前上下文情境下的表征。（这与我们在图像表示中，用 CNN 最后一个卷积层作为表示的思路类似）

具体而言，其流程如下：

1. 在大语料库上训练一个双向 RNN
2. 将感兴趣的句子正向/反向输入这个预训练的 RNN
3. 最后的词的嵌入由两种情况下 RNN 的隐藏层拼接起来构成

3.4、BERT

ELMo 嵌入也有一些缺陷：

• RNN 记忆能力有限，难以捕获长距离依赖
• RNN 只允许顺序执行操作，难以并行化

BERT（Bidirectional Encoder Representations from Transformers），其与 RNN 不同，采用的是基于 Transformer 的“全连接”结构。相比于传统的全连接层，Transformer 是一种依赖于自注意力机制的架构，能够有效处理序列数据。

---

BERT 模型的预训练任务可以分为两个部分：

• Masked Language Model（MLM）：在输入的句子中随机 Mask （掩盖、隐藏）掉一些词，然后训练模型去预测这些 mask 掉的词
• Next Sentence Prediction（NSP）：在输入的句子对中，训练模型去预测第二个句子是否是第一个句子的下一个句子

每次输入两个句子，用特殊的符号区分这两个句子，然后将两个句子拼接起来输入模型，同时进行 MLM 和 NSP 任务：

---

BERT 模型最终得到的嵌入由三个部分的和构成：

• Token Embeddings：输入的词的嵌入。
• Segment Embeddings：区分输入中的不同句子。例如，第一个句子的嵌入为 0，第二个句子的嵌入为 1。
• Position Embeddings：位置嵌入，用于区分不同位置的词。其公式为：$\text{PE}_{(pos, i)}=\sin(pos/10000^{2i/d})$

第十六讲 推荐系统

1、引入

对推荐问题进行建模，记$X$为用户集合，$S$为物品集合，$R$为用户对物品的效用矩阵（Utility Matrix），$R_{ij}$可以理解为用户$i$对物品$j$的喜爱程度。效用函数$u:X\times S\rightarrow \mathbb{R}$。

在推荐问题中，有以下几个关键问题：

• 收集可以获得的数据，填充效用矩阵
• 外推无法观测/未知的数据，尤其是关注高的效用值
• 评估外推方法的好坏

---

对于第一个问题，可以去直接询问（Explit Feedback）用户对物品的评分，也可以通过用户的行为（Implicit Feedback）来推断用户对物品的喜好。例如用户下单购买某商品，相比只是浏览，反映着较高的喜爱程度。

关于外推其他效用值。首先，由于用户不可能购买过所有商品，所以效用矩阵是稀疏的。也就是说，用户购买商品的记录十分有限，要面临冷启动问题。其次，对于新用户或者是新商品，根本没有任何历史记录，很难做外推。

2、基于内容的推荐

Content-Based Recommendation，这是一种不依赖于效用矩阵的推荐方法。其基本思想是根据该用户打出高分的物品，推荐与之相似的物品，例如推荐相同类型/演员/风格的电影。

---

为了判断两个物品的相似性，首先我们要为物品创建一个档案（Profile），也即代表物品的特征向量。对于电影来说，档案可以代表导演/标题/演员等；对于文本来说，可以是关键词等。我们需要挑选出最能代表物品的特征，例如对于文本，可以用我们之前提到的 TFIDF 方法。

然后两个物品之间的相似度，可以用档案的余弦相似度来衡量，也即两个向量夹角的余弦。

---

优点：

• 无需其他用户的数据，没有稀疏以及冷启动的问题。
• 每个用户有一个独立的推荐状态，不易受到其他用户的影响。
• 有可解释性

缺点：

• 找到合适的特征比较困难
• 新用户无历史记录，难以推荐
• 过度专一化，无法跟上用户的新兴趣，也无法利用其它用户的评价来辅助判断。

3、协同过滤

Collaborative Filtering

3.1、用户-用户协同过滤

其灵感是，如果有一批人 $N$ 和 $x$ 一样都买了某件商品 A，且 $N$ 中大部分人还会买 B，可以推测 $x$ 也会对 B 感兴趣。

记$x$对所有商品的评分为$\boldsymbol{r}_x$，$I_{x, y}$是$x$和$y$都打过分的商品的集合，可以引入皮尔逊相关系数（Pearson correlation coefficient）：

$$\text{sim}(x, y)=\frac{\sum_{i\in I_{xy}}(r_{xi}-\bar{r}_x)(r_{yi}-\bar{r}_y)}{\sqrt{\sum_{i\in I_{xy}}(r_{xi}-\bar{r}_x)^2}\sqrt{\sum_{i\in I_{xy}}(r_{yi}-\bar{r}_y)^2}}$$

这里减去平均值是为了避免将没评分的结果（0）视为最负面的结果，所以减去平均值后，正面的评分为正，负面的评分为负，更能够反映用户的喜好。

于是可以这样做外推：

$$\hat{r}_{x i}=\bar{r}_x+\frac{\sum_{y\in N} \text{sim}(x, y)(r_{yi}-\bar{r}_y)}{\sum_{y\in N} \text{sim}(x, y)}$$

3.2、物品-物品协同过滤

这种方法的灵感来源于，如果用户 $x$ 喜欢物品 A，那么他也可能喜欢和 A 相似的物品 B。

其与上面那种方法是类似的，只是这里是计算物品之间的相似度，而不是用户之间的相似度：

$$r_{x i}=b_{x i}+\frac{\sum_{j\in I_{x}}\text{sim}(i, j)(r_{xj}-b_{xj})}{\sum_{j\in I_{x}}\text{sim}(i, j)}$$

这里$I_x$代表用户$x$评分过的物品集合。其中$b_{x i}=\mu+b_x+b_i$，$\mu$是所有评分的平均值，$b_x$是用户$x$的评分偏差（个人与大众的偏差），$b_i$是物品$i$的评分偏差（大众在物品$i$上与其他物品的偏差）。

实际中，物品-物品联合推荐表现要比用户-用户联合推荐好，因为物品的特征和相似性更容易捕获，且相对单一。而用户的品味和爱好是多样的。

3.3、分析

协同过滤的优点：对于各种物品都适用，无需去挑选特征。

缺点：冷启动问题，对于新用户和新物品（First rater），无法推荐。且对于稀疏数据，效果不佳。而且倾向于推荐热门物品，缺乏多样性。

实践中，一般都结合使用上述方法。

4、基于矩阵分解的推荐

考虑效用矩阵$\boldsymbol{U}\in \mathbb{R}^{m\times n}$，其中$m$是用户数，$n$是物品数。我们希期找到两个矩阵$\boldsymbol{P}^T\in \mathbb{R}^{m\times k}$和$\boldsymbol{Q}\in \mathbb{R}^{n\times k}$，使得$\boldsymbol{U}\approx \boldsymbol{P}^T\boldsymbol{Q}$。

我们希望近似的结果尽可能接近，并加上一些正则项，所以可以目标是最小化：

$$\min_{\boldsymbol{P}, \boldsymbol{Q}}\sum_{i, j}(r_{ij}-\boldsymbol{p}_i^T\boldsymbol{q}_j)^2+\lambda(\Vert \boldsymbol{p}_i\Vert^2+\Vert \boldsymbol{q}_j\Vert^2)$$

仅考虑有评分的项，通过梯度下降来进行训练。最终可以利用$\boldsymbol{p}^T\boldsymbol{q}$来预测未知的评分。

第十七讲 异常检测

Anomaly Detection，有时也称为离群点检测或新颖性检测。

1、引入

一般来说，在一个数据集中，绝大部分的样本都是“相同的”，我们称这些样本为正常样本。剩下的样本与正常样本们往往有很大的不同，我们称这些样本为异常样本。

异常样本与正常样本之间差异也是多种多样的，仅通过一个两个显式的标准很难判断某个样本是否异常，这也是异常检测的难点。

网络入侵检测、信用卡欺诈检测、罕见疾病诊断、工业损伤检测等问题，都可以看作是异常检测问题。原来解决这些问题的方法，往往都是依靠已有的或者已出现的异常：如果新的样本和以前出现过的异常样本相似，那么就可以判断这个样本也是异常的。这种方法一个最大的问题是，对于一种全新的异常，是检测不出来的。这也是以前的异常检测方法的一个最大的缺陷。

---

异常的种类包括：

• 点异常：只通过样本本身就能判断的异常（相对接下来的上下文异常或者整体异常而言）
• 上下文异常：样本本身看起来正常，只有放到一个上下文中才能看出的异常。比如一个波正常应该是波峰的区域，出现了波谷：
  
• 整体异常：单独看或者在上下文中看都是正常的，但是整体来看是异常的。比如心电图中的某一段变为直线，这段直线在周围正常的波形中就显得异常：
  

2、基于距离的异常检测

异常点也被称为离群点，也就是距离“大部队”比较“远”的点。基于距离的异常检测方法，就是通过计算样本点与其他样本点的距离，更具体的说，是离第$k$个最邻近邻居的距离，来判断样本点是否异常。这个距离越大，说明越有可能是异常。

优点：

• 简单、容易实现
• 可解释性强，符合直觉

缺点：

• 需要知道样本点两两之间的距离，复杂度高达$O(n^2)$
• 对$k$的选择敏感
• 对于高维数据，难以找到一种合适的距离度量

3、基于密度的异常检测

另一角度看，离群点旁边的点总是比较少，或者说异常点总是落在低密度的区域。

基于密度的异常检测，首先根据大量的正常样本，估计出一个概率密度分布$\hat{p}(x)$，然后对于一个新的样本$x$，计算其概率密度$p(x)$，如果$p(x)$小于某个阈值，就认为这个样本是异常的。

---

核密度估计（Kernel Density Estimation）是一种常用的密度估计方法。这种方法中，一组样本$\boldsymbol{x}_i$的概率密度函数可以写为：

$$\hat{p}(\boldsymbol{x})=\frac {1}{Nh} \sum_{i=1}^n K(\frac{\boldsymbol{x}-\boldsymbol{x}_i}{h})$$

其中$K(\cdot)$是某个核函数，$h$是一个参数，用于控制分布的平滑程度（带宽）。

KDE 的缺点是，对$h$的选择敏感，且在高维数据上的表现不佳。

---

另一种方法是，用已知的分布去拟合数据，类似于之前的高斯混合模型。概率密度分布可写为：

$$\hat{p}(\boldsymbol{x})=\mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma})$$

或者是：

$$\hat{p}(\boldsymbol{x})=\sum_{i=1}^k \pi_i \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)$$

其中参数$\boldsymbol{\theta}$通过最大似然估计得到。

这种方法好坏受到选择分布本身的表达能力的限制，且同样在高维数据上表现不佳。

---

针对在高维数据上表现不佳的问题，提出了两阶段法：

1. 通过某种方式（PCA、自编码器等）对数据进行降维/学习到一个低维的表示
2. 利用 KDE 或者已知分布拟合，对降维后的数据进行密度估计

---

用大量正常样本训练深度生成模型（如 VAE、GAN）等，也可以得到一个概率密度分布。然后用这个分布来判断新样本是否异常。

4、基于重建的异常检测

在大量正常样本上训练一个编码——解码模型。编码器将输入的样本映射到一个低维的表示，训练解码器能够将这个低维表示重建回原始的样本。

由于是在正常样本上训练的，所以对于正常样本，重建出来的样本应该和原始样本相似；而对于异常样本，重建出来的样本应该和原始样本有较大的差异。依据这个原理，我们可以用重建误差来判断样本是否异常。

其实，这种方法的本质，也是在寻找正常样本的某种特征或者说低维表示（训练编码器），只是利用特征/低维表示的方式有所不同。

5、单类分类器

由于大量的数据都比较“靠近”，可以想象画一个圈，将大部分的数据包含在里面，圈外的数据就是异常的。也就是说，只划分一个类出来，所以这种方法叫做单类分类器。

---

首先考虑找到一个最小的超球，能将所有的样本点包含进去。设超球的半径为$r$，球心为$\boldsymbol{c}$，则这个问题可以写为：

$$\min_{\boldsymbol{c}, r} r^2, \text{ s.t. } \Vert \phi(\boldsymbol{x}_i)-\boldsymbol{c}\Vert^2\leqslant r^2$$

其中$\phi(\cdot)$是任意一种非线性映射。

显然，这样的超球很容易受到离群点的影响。为了将离群点包含进去，不得不增大超球的半径。

---

接下来，考虑松弛，将这些离群点“放出去”。引入一个松弛变量$\xi_i$，则问题可以写为：

$$\min_{\boldsymbol{c}, r, \boldsymbol{\xi}} r^2+\frac{1}{\nu n}\sum_{i=1}^n \xi_i, \text{ s.t. } \Vert \phi(\boldsymbol{x}_i)-\boldsymbol{c}\Vert^2\leqslant r^2+\xi_i, \xi_i\geqslant 0$$

其中$\nu$是一个超参数，用于控制松弛的程度。当$\nu$趋于 0 时，这个问题就退化为前面的问题。（很类似于软间隔 SVM 的形式）

通过这样的超球，就可以按照一开始的想法，将超球内的样本划分为正常样本，超球外的样本划分为异常样本。

---

$\phi(\cdot)$可以是某个核函数，这样优化问题可以通过解其对偶形式解决。这就完全类似于 SVM 的形式了。

$\phi(\cdot)$还可以是一个神经网络，可以通过用 SGD 来优化以下无约束的损失函数：

$$L=r^2+\frac{1}{\nu n}\sum_{i=1}^n \max(0, \Vert \phi(\boldsymbol{x}_i)-\boldsymbol{c}\Vert^2-r^2)$$

6、评估指标

如何评估异常检测的好坏？

根据样本实际的正常与否以及预测结果，可以得出下面这个表格：

四类样本的数量，用其名字的首字母表示，例如 TP 代表 True Positive。

一种直接的想法是用预测的准确率来评估：

$$\text{AC}=\frac{TP+TN}{TP+TN+FP+FN}$$

但是，这种指标对于异常检测来说并不合适，因为异常样本往往是少数，而正常样本是多数。粗暴地全部认为是正确样本，就能得到一个很高的准确率。

6.1、ROC 曲线

考虑将正常样本预测为正常的比例（True Positive Rate，也称为召回率）$\text{TPR}=TP/(TP+FN)$，以及将异常样本预测为正常的比例（False Positive Rate）$\text{FPR}=FP/(FP+TN)$。考虑采用不同的分类阈值，得到多组 TPR 和 FPR。然后以 TPR 为纵轴，FPR 为横轴，做出曲线图，这个曲线就称为ROC 曲线（Receiver Operating Characteristic Curve）：

可以想象，某个分类阈值对应的点越靠近左上角，说明其能在正确识别出绝大部分正常样本的同时，只将很少的异常样本误判为正常样本，也就说明这个分类阈值更好。

而对于整个异常检测方法而言，可以用 ROC 曲线下的面积（Area Under ROC Curve，AUROC）来评估。AUROC 越大，说明曲线越靠近左上角，也就说明每个分类阈值下表现都很好，也就说明这个异常检测方法越好。

随机预测的情况下，TPR 始终为 0.5，对应 AUROC 为 0.5。所以可以 0.5 作为基准，来评估异常检测方法的好坏。

6.2、PR 曲线

考虑召回率$\text{Recall}=TP/(TP+FN)$和精确率$\text{Precision}=TP/(TP+FP)$。同样，考虑不同的分类阈值，得到多组召回率和精确率。以召回率为横轴，精确率为纵轴，做出曲线图，这个曲线就称为PR 曲线（Precision-Recall Curve）：

某个分类阈值对应的点越靠近右上角，说明不但能够召回大部分正常样本（横坐标大，召回率高），还能较好的剔除异常样本（纵坐标大，精确率高），也就说明这个分类阈值更好。

对于整个异常检测方法而言，可以用 PR 曲线下的面积（Area Under PR Curve，AUPR）来评估。AUPR 越大，说明曲线越靠近右上角，也就说明每个分类阈值下表现都很好，也就说明这个异常检测方法越好。

随机检测的 AUPR 不一定为 0.5，可以直接将用了异常检测方法的 AUPR 与随机检测的 AUPR 进行比较，如果更大，说明这个异常检测方法是有效的。

6.3、F1 值

这是一个形式和使用更加简单的指标。F1 值是精确率和召回率的调和平均：

$$F1=\frac{2}{\text{Precision}^{-1}+\text{Recall}^{-1}}=2\cdot \frac{\text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}$$

F1 值越大，说明精确率和召回率都很高，也就说明这个异常检测方法越好。