说在前面
动手写一个这个的起因是,看见舍友 A 在做密码学实验。这学期选课的时候,想着自己都已经学过组合数学与数论、代数结构了,把密码学的先修课程都学了(虽然学得一坨),选个密码学也很合理吧。结果因为时间冲突,遗憾没能选上。但离奇的是,和我一个教学班的另一位舍友 B(课程安排基本相同)成功选上了密码学理论,让我感到非常困惑。
这个密码学实验的平台现代密码学实验 (还是这学期助教手搓的(助教还是铁血二次元,域名甚至就带 akarin),而且前期因为 bug 太多不好用,还被狠狠吐槽。Matrix 一位也选了密码学的同学当场质疑:“为什么不用 Matrix!”不过助教祭天多次之后,目前实验平台用着也是没啥大问题。
最开始是看到舍友 A 在做上面的实验 1-1:维吉尼亚密码分析,教他写的时候又被他气晕。把想法转化为代码的能力实在是太差,不如我自己上去写。然后因为没有上过理论课,很多前置知识都是现查的,当晚并没有 AC。
这次看到 A 又在与密码学实验鏖战,我瞟了一眼,原来是实验 2-1:有限域运算。本来上次被勾引了一下兴趣就起来了,于是索性借他的号准备代打(误),于是就有了这份代码和这篇文章。
实验的简要描述以及完整代码已经放到了 Github 上:Smallorange666/Finite-field-operations 。实验平台上有详细描述以及助教提供的指导和提示信息。
处理输入输出
本次实验的输入输出都是二进制数据,大一学 C 语言的时候提到fopen中关于打开模式的参数b表示以二进制读写文件,终于有了实践机会。
贴心的助教还提供了一个ONLINE_JUDGE的编译参数,再编写一些宏,就可以实现本地调试和上评测机无缝衔接:
1 2 3 4 5 6 7 8 9 10 11 12 13 #ifdef ONLINE_JUDGE #define in stdin #define out stdout #endif int main (void ) { #ifndef ONLINE_JUDGE FILE *in = fopen("input.bin" , "rb" ); FILE *out = fopen("output.bin" , "wb" ); #endif }
一开始还对数据的读入感到疑惑。因为是输入是二进制,读的时候用uint64_t读,会不会导致“读反”呢。其实大可不必担心:
第一:数据本身就是以二进制小端序给出的,这本来就与计算机的存储方式一样。而我们用fread读入,程序只知道是一个个字节,会原样按顺序读入,最后将其视为一个uint64_t整体。我们对这个uint64_t进行操作的时候,不用在意其内部字节的排列,因为说白了这就是一个整数嘛,该怎么样就是怎么样,底层交给计算机去处理。
例如,数据是0x12 0x34 0x56 0x78,用fread读入到uint32_t中,如果你试图将其转换为uint8_t *,然后逐字节输出,得到的自然还是0x12 0x34 0x56 0x78。如果你直接以十六进制形式输出这个uint32_t的值,得到的应该是0x78563412。
如果你想把这个uint32_t的低 16 位变为 0,直接与上0xFFFF0000即可。而不是想到,“低 16 位”放在第一和第二个字节,所以应该与上0x0000FFFF,这恰恰是错误的做法。
运算实现
有限域的基本知识不再这里赘述(也述不出来),可以看看这篇:密码学基础 有限域
在本次实验中,你只需要关心:有限域F 2 131 F_{2^{131}} F 2 131 a ( x ) = ∑ i = 0 130 a i x i a(x)=\sum_{i=0}^{130}a_ix^i a ( x ) = ∑ i = 0 130 a i x i a i ∈ { 0 , 1 } a_i\in\{0,1\} a i ∈ { 0 , 1 } uint64_t 来存储(类似于压位高精度的思想)这个 131 位的二进制数,剩余的位置 0 即可。每一个uint64_t称为一个字 。
因为系数是在有限域内的,所以系数之间的加法等价与异或运算,乘法等价于与运算 。
加法
也即两个 131 位二进制数逐位异或,也可以拆分为三个字的异或:
1 2 3 4 5 6 7 void gf_add (uint64_t res[5 ], const uint64_t a[5 ], const uint64_t b[5 ]) { for (int i = 0 ; i < 3 ; i++) { res[i] = a[i] ^ b[i]; } }
乘法
普通乘法
最一般的做法就是普通的多项式相乘,模拟手工乘法,假设有两个多项式:
a ( x ) = ∑ i = 0 130 a i x i , b ( x ) = ∑ i = 0 130 b i x i a(x)=\sum_{i=0}^{130}a_ix^i, b(x)=\sum_{i=0}^{130}b_ix^i
a ( x ) = i = 0 ∑ 130 a i x i , b ( x ) = i = 0 ∑ 130 b i x i
则有:
c ( x ) = a ( x ) ∗ b ( x ) = ∑ i = 0 130 ∑ j = 0 130 a i b j x i + j c(x)=a(x)*b(x)=\sum_{i=0}^{130}\sum_{j=0}^{130}a_ib_jx^{i+j}
c ( x ) = a ( x ) ∗ b ( x ) = i = 0 ∑ 130 j = 0 ∑ 130 a i b j x i + j
容易知道结果 c ( x ) c(x) c ( x ) x i x^i x i ∑ j ∑ k a j b k \sum_{j}\sum_k a_jb_k ∑ j ∑ k a j b k j + k = i j+k=i j + k = i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void gf_mul_trivial (uint64_t res[5 ], const uint64_t a[5 ], const uint64_t b[5 ]) { uint64_t tem[5 ] = {0 }; for (int i = 0 ; i < 131 ; i++) { for (int j = 0 ; j < 131 ; j++) { int i1 = i / 64 , i2 = i % 64 ; int j1 = j / 64 , j2 = j % 64 ; int ij1 = (i + j) / 64 , ij2 = (i + j) % 64 ; const uint64_t mask = 1 ; uint64_t ai = 0 , bj = 0 ; if (a[i1] & (mask << i2)) ai = 1 ; if (b[j1] & (mask << j2)) bj = 1 ; tem[ij1] ^= (ai & bj) << ij2; } } gf_mod(res, tem); }
由于我们是用 64 位整数数组储存多项式,所以要考虑第 i i i i1、i2就分别是字偏移量和位偏移量,其余变量也是类似的。
位运算乘法
通过简单的位运算,也可以实现乘法。因为:
c ( x ) = a ( x ) b ( x ) = ∑ i = 0 130 b i a ( x ) x i c(x)=a(x)b(x)=\sum_{i=0}^{130}b_i a(x)x^i
c ( x ) = a ( x ) b ( x ) = i = 0 ∑ 130 b i a ( x ) x i
对于多项式 a ( x ) a(x) a ( x ) x i x^i x i b i b_i b i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void gf_mul_bit (uint64_t res[5 ], const uint64_t a[5 ], const uint64_t b[5 ]) { uint64_t tem[5 ] = {0 }; uint64_t b_[5 ] = {0 }; for (int i = 0 ; i < 5 ; i++) { uint64_t mask = 1 ; for (int j = 0 ; j < 64 ; j++) { if (a[i] & mask) { left_shift(b_, b, i * 64 + j); for (int k = 0 ; k < 5 ; k++) tem[k] = tem[k] ^ b_[k]; } mask <<= 1 ; } } gf_mod(res, tem); }
这里就是遍历a的每一位,如果这一位是 1,就将b左移相应的位数,然后与结果异或。
Karatsuba 算法
n n n O ( n 2 ) O(n^2) O ( n 2 ) O ( n ) O(n) O ( n ) Karatsuba 算法 ,该算法的原理是将大数拆成几部分,分别计算各部分的乘积,最后合并结果。本实验中,天然进行了划分,将原数划分为了三个字。
记原比特串为 A A A
A = A 2 2 128 + A 1 2 64 + A 0 A=A_22^{128}+A_12^{64}+A_0
A = A 2 2 128 + A 1 2 64 + A 0
其中 A 2 , A 1 , A 0 A_2, A_1, A_0 A 2 , A 1 , A 0
于是,根据 Karatsuba 算法的思想,两个比特串相乘可以写为:
A B = ( A 2 2 128 + A 1 2 64 + A 0 ) ( B 2 2 128 + B 1 2 64 + B 0 ) = A 2 B 2 2 256 + ( A 2 B 1 + A 1 B 2 ) 2 192 + ( A 2 B 0 + A 0 B 2 + A 1 B 1 ) 2 128 + ( A 1 B 0 + A 0 B 1 ) 2 64 + A 0 B 0 = A 2 B 2 2 256 + [ ( A 1 + A 2 ) ( B 1 + B 2 ) − A 1 A 2 − B 1 B 2 ] 2 192 + [ ( A 0 + A 2 ) ( B 0 + B 2 ) − A 0 B 0 − A 2 B 2 + A 1 B 1 ] 2 128 + [ ( A 0 + A 1 ) ( B 0 + B 1 ) − A 0 A 1 − B 0 B 1 ] 2 64 + A 0 B 0 \begin{split}
AB&=(A_2 2^{128}+A_1 2^{64}+A_0)(B_2 2^{128}+B_1 2^{64}+B_0)\\
&=A_2B_2 2^{256}+(A_2B_1+A_1B_2) 2^{192}+(A_2B_0+A_0B_2+A_1B_1) 2^{128}\\
&+(A_1B_0+A_0B_1) 2^{64}+A_0B_0\\
&=A_2B_2 2^{256}+[(A_1+A_2)(B_1+B_2)-A_1A_2-B_1B_2] 2^{192}\\
&+[(A_0+A_2)(B_0+B_2)-A_0B_0-A_2B_2+A_1B_1] 2^{128}\\
&+[(A_0+A_1)(B_0+B_1)-A_0A_1-B_0B_1] 2^{64}+A_0B_0
\end{split}
A B = ( A 2 2 128 + A 1 2 64 + A 0 ) ( B 2 2 128 + B 1 2 64 + B 0 ) = A 2 B 2 2 256 + ( A 2 B 1 + A 1 B 2 ) 2 192 + ( A 2 B 0 + A 0 B 2 + A 1 B 1 ) 2 128 + ( A 1 B 0 + A 0 B 1 ) 2 64 + A 0 B 0 = A 2 B 2 2 256 + [( A 1 + A 2 ) ( B 1 + B 2 ) − A 1 A 2 − B 1 B 2 ] 2 192 + [( A 0 + A 2 ) ( B 0 + B 2 ) − A 0 B 0 − A 2 B 2 + A 1 B 1 ] 2 128 + [( A 0 + A 1 ) ( B 0 + B 1 ) − A 0 A 1 − B 0 B 1 ] 2 64 + A 0 B 0
记基本乘积:
P 1 = A 0 B 0 , P 1 = A 1 B 1 , P 2 = A 2 B 2 P_1=A_0B_0, P1=A_1B_1, P_2=A_2B_2
P 1 = A 0 B 0 , P 1 = A 1 B 1 , P 2 = A 2 B 2
记基本和:
S 0 = A 0 + A 1 , S 1 = A 1 + A 2 , S 2 = A 0 + A 2 , S 3 = B 0 + B 1 , S 4 = B 1 + B 2 , S 5 = B 0 + B 2 S_0=A_0+A_1, S_1=A_1+A_2, S_2=A_0+A_2, S_3=B_0+B_1, S_4=B_1+B_2, S_5=B_0+B_2
S 0 = A 0 + A 1 , S 1 = A 1 + A 2 , S 2 = A 0 + A 2 , S 3 = B 0 + B 1 , S 4 = B 1 + B 2 , S 5 = B 0 + B 2
然后计算交叉和:
P 3 = S 0 S 3 − P 0 − P 1 , P 4 = S 2 S 5 − P 0 − P 2 , P 5 = S 1 S 4 − P 1 − P 2 P_3=S_0S_3-P_0-P_1, P_4=S_2S_5-P_0-P_2, P_5=S_1S_4-P_1-P_2
P 3 = S 0 S 3 − P 0 − P 1 , P 4 = S 2 S 5 − P 0 − P 2 , P 5 = S 1 S 4 − P 1 − P 2
注意 P i P_i P i S i S_i S i P i h P_{ih} P ih P i P_i P i P i l P_{il} P i l P i P_i P i
uint64_t[4]uint64_t[3]uint64_t[2]uint64_t[1]uint64_t[0]
P 2 l + P 5 h P_{2l}+P_{5h} P 2 l + P 5 h P 5 l + ( P 1 + P 4 ) h P_{5l}+(P_1+P_4)_h P 5 l + ( P 1 + P 4 ) h ( P 1 + P 4 ) l + P 3 h (P_1+P_4)_l+P_{3h} ( P 1 + P 4 ) l + P 3 h P 3 l + P 0 h P_{3l}+P_{0h} P 3 l + P 0 h P 0 l P_{0l} P 0 l
计算基本乘积、基本和、交叉和这样的,64 位的加法乘法,可以利用 SIMD (Single Instruction Multiple Data,单指令多数据)指令 进行加速。实验描述中提示,可以参考这篇论文 ECC2-131 的并行 Pollard rho 算法实现分析 。我实现的具体过程进行了修改,并不完全与论文一致。
于是可以写出:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 void gf_mul_simd (uint64_t res[5 ], const uint64_t a[5 ], const uint64_t b[5 ]) { __m128i A0 = _mm_set_epi64x(0 , a[0 ]); __m128i A1 = _mm_set_epi64x(0 , a[1 ]); __m128i A2 = _mm_set_epi64x(0 , a[2 ]); __m128i B0 = _mm_set_epi64x(0 , b[0 ]); __m128i B1 = _mm_set_epi64x(0 , b[1 ]); __m128i B2 = _mm_set_epi64x(0 , b[2 ]); __m128i S0 = _mm_xor_si128(A0, A1); __m128i S1 = _mm_xor_si128(A1, A2); __m128i S2 = _mm_xor_si128(A0, A2); __m128i S3 = _mm_xor_si128(B0, B1); __m128i S4 = _mm_xor_si128(B1, B2); __m128i S5 = _mm_xor_si128(B0, B2); __m128i P0 = _mm_clmulepi64_si128(A0, B0, 0x00 ); __m128i P1 = _mm_clmulepi64_si128(A1, B1, 0x00 ); __m128i P2 = _mm_clmulepi64_si128(A2, B2, 0x00 ); __m128i P3 = _mm_xor_si128(_mm_clmulepi64_si128(S0, S3, 0x00 ), _mm_xor_si128(P0, P1)); __m128i P4 = _mm_xor_si128(_mm_clmulepi64_si128(S2, S5, 0x00 ), _mm_xor_si128(P0, P2)); __m128i P5 = _mm_xor_si128(_mm_clmulepi64_si128(S1, S4, 0x00 ), _mm_xor_si128(P1, P2)); uint64_t tem[5 ] = {0 }; tem[0 ] = _mm_extract_epi64(P0, 0 ); tem[1 ] = _mm_extract_epi64(P3, 0 ) ^ _mm_extract_epi64(P0, 1 ); tem[2 ] = _mm_extract_epi64(_mm_xor_si128(P1, P4), 0 ) ^ _mm_extract_epi64(P3, 1 ); tem[3 ] = _mm_extract_epi64(P5, 0 ) ^ _mm_extract_epi64(_mm_xor_si128(P1, P4), 1 ); tem[4 ] = _mm_extract_epi64(P2, 0 ) ^ _mm_extract_epi64(P5, 1 ); gf_mod(res, tem); }
说明一下上面的代码:
_mm_set_epi64x(0, a[0]):将a[0]设置到一个 128 位向量__m128的低 64 位中
_mm_xor_si128(): 对两个 128 位向量进行按位异或操作
_mm_clmulepi64_si128(A0, B0, 0X00):取A0和B0向量的低 64 位进行无进位乘法 ,用到了论文中提到的 PCLMULQDQ(Packed Carry-Less Multiplication Quadword)指令,是 Intel 的 SSE4.2 指令集的一部分。
_mm_extract_epi64(P0, _):从 128 位向量中提取 64 位整数。第二个参数设置为 0 时取低 64 位,第二个参数设置为 1 时取高 64 位。
上面这段代码用到了 SIMD 中的 SSE 和 AES-NI 指令集,如果要在本地编译运行,首先需要确保你的 CPU 支持这些指令集,然后添加编译参数 -march=native -mtune=native以启用所有检测到的指令集。
取模
思路参考了Guide to elliptic curve cryptography 一书中 2.3.5 节提到的:对于特殊形式的不可约多项式,可以简单地通过位运算的方式,快速取模。(电子书可自行寻找资源)
我们利用相同的思路,因为不可约多项式为 f ( x ) = x 131 + x 13 + x 2 + x + 1 f(x)=x^{131}+x^{13}+x^2+x+1 f ( x ) = x 131 + x 13 + x 2 + x + 1
x 131 ≡ x 13 + x 2 + x + 1 m o d f ( x ) x^{131}\equiv x^{13}+x^2+x+1 \mod f(x)
x 131 ≡ x 13 + x 2 + x + 1 mod f ( x )
要取模的数假设为:
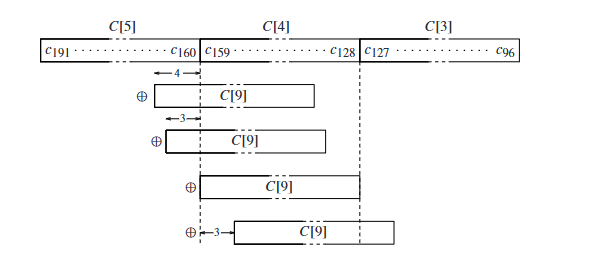
C [ 4 ] C[4] C [ 4 ] C [ 3 ] C[3] C [ 3 ] C [ 2 ] C[2] C [ 2 ] C [ 1 ] C[1] C [ 1 ] C [ 0 ] C[0] C [ 0 ]
a 319 … a 256 a_{319}\dots a_{256} a 319 … a 256 a 255 … a 192 a_{255}\dots a_{192} a 255 … a 192 a 191 … a 128 a_{191}\dots a_{128} a 191 … a 128 a 127 a 126 … a 64 a_{127}a_{126}\dots a_{64} a 127 a 126 … a 64 a 63 a 62 … a 0 a_{63}a_{62}\dots a_{0} a 63 a 62 … a 0
考虑对 C [ 3 ] C[3] C [ 3 ]
{ a 255 x 255 ≡ a 255 x 137 + a 255 x 126 + a 255 x 125 + a 255 x 124 m o d f ( x ) a 254 x 254 ≡ a 254 x 136 + a 254 x 125 + a 254 x 124 + a 254 x 123 m o d f ( x ) ⋮ a 192 x 192 ≡ a 192 x 74 + a 192 x 63 + a 192 x 62 + a 192 x 61 m o d f ( x ) \begin{cases}
a_{255}x^{255}\equiv & a_{255}x^{137}+a_{255}x^{126}+a_{255}x^{125}+a_{255}x^{124}&\mod f(x)\\
a_{254}x^{254}\equiv & a_{254}x^{136}+a_{254}x^{125}+a_{254}x^{124}+a_{254}x^{123}&\mod f(x)\\
&\vdots\\
a_{192}x^{192}\equiv & a_{192}x^{74}+a_{192}x^{63}+a_{192}x^{62}+a_{192}x^{61}&\mod f(x)
\end{cases}
⎩ ⎨ ⎧ a 255 x 255 ≡ a 254 x 254 ≡ a 192 x 192 ≡ a 255 x 137 + a 255 x 126 + a 255 x 125 + a 255 x 124 a 254 x 136 + a 254 x 125 + a 254 x 124 + a 254 x 123 ⋮ a 192 x 74 + a 192 x 63 + a 192 x 62 + a 192 x 61 mod f ( x ) mod f ( x ) mod f ( x )
这些式子累加起来,左边就是C [ 3 ] C[3] C [ 3 ] C [ 3 ] C[3] C [ 3 ]
于是,我们可以通过位运算来实现快速取模。论文 中有用这种思想取模的伪代码,但是错误的 。正确的代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void gf_mod (uint64_t res[5 ], const uint64_t a[5 ]) { uint64_t e[5 ]; for (int i = 0 ; i < 5 ; i++) { e[i] = a[i]; } for (int i = 4 ; i >= 3 ; i--) { uint64_t t = e[i]; e[i - 3 ] = e[i - 3 ] ^ (t << 61 ) ^ (t << 62 ) ^ (t << 63 ); e[i - 2 ] = e[i - 2 ] ^ (t << 10 ) ^ (t >> 1 ) ^ (t >> 2 ) ^ (t >> 3 ); e[i - 1 ] = e[i - 1 ] ^ (t >> 54 ); } uint64_t t = e[2 ] >> 3 ; res[0 ] = e[0 ] ^ (t << 13 ) ^ t ^ (t << 1 ) ^ (t << 2 ); res[1 ] = e[1 ] ^ (t >> 51 ); res[2 ] = e[2 ] & 0x7 ; }
只要能理解“比特串移动”,剩下的都是小学数学和信息的问题。
平方
复用乘法
即直接调用乘法,于是有:
1 2 3 4 void gf_pow2_mul (uint64_t res[5 ], const uint64_t a[5 ]) { gf_mul_simd(res, a, a); }
位运算
类似于位运算做乘法的思路。但由于是平方,可以消去许多项:
c ( x ) = a ( x ) ∗ a ( x ) c(x)=a(x)*a(x)
c ( x ) = a ( x ) ∗ a ( x )
考虑 x i x^i x i ∑ j = 0 i a j a i − j \sum_{j=0}^ia_ja_{i-j} ∑ j = 0 i a j a i − j i i i
∑ j = 0 i a j a i − j = ∑ j = 0 i / 2 ( a j a i − j + a j a i − j ) + a i / 2 a i / 2 \sum_{j=0}^ia_ja_{i-j}=\sum_{j=0}^{i/2}(a_ja_{i-j}+a_ja_{i-j})+a_{i/2}a_{i/2}
j = 0 ∑ i a j a i − j = j = 0 ∑ i /2 ( a j a i − j + a j a i − j ) + a i /2 a i /2
由有限域的性质,两相同数相加等于两相同数异或,消除;两相同数相乘等于相与,就是原数,则 x i x^i x i a i / 2 a_{i/2} a i /2
同理, i i i
综上:
c ( x ) = a ( x ) ∗ a ( x ) = ∑ i = 0 130 a i x 2 i c(x)=a(x)*a(x)=\sum_{i=0}^{130}a_ix^{2i}
c ( x ) = a ( x ) ∗ a ( x ) = i = 0 ∑ 130 a i x 2 i
于是可以写出:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 void gf_pow2_bit (uint64_t res[5 ], const uint64_t a[5 ]) { uint64_t tem[5 ] = {0 }; for (int i = 0 ; i < 5 ; i++) { for (int j = 0 ; j < 64 ; j++) { int i_ = ((i * 64 + j) * 2 ) / 64 ; int j_ = (i * 64 + j) * 2 % 64 ; uint64_t mask = 1 ; if (a[i] & (mask << j)) { tem[i_] |= mask << j_; } } } gf_mod(res, tem); }
Karatsuba 算法
与乘法是相同的思路,同样利用 Karatsuba 算法,推导略去。由于是相同的数相乘,仅需计算三个交叉和:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void gf_pow2_simd (uint64_t res[5 ], const uint64_t a[5 ]) { __m128i A0 = _mm_set_epi64x(0 , a[0 ]); __m128i A1 = _mm_set_epi64x(0 , a[1 ]); __m128i A2 = _mm_set_epi64x(0 , a[2 ]); __m128i P0 = _mm_clmulepi64_si128(A0, A0, 0x00 ); __m128i P1 = _mm_clmulepi64_si128(A1, A1, 0x00 ); __m128i P2 = _mm_clmulepi64_si128(A2, A2, 0x00 ); uint64_t tem[5 ] = {0 }; tem[0 ] = _mm_extract_epi64(P0, 0 ); tem[1 ] = _mm_extract_epi64(P0, 1 ); tem[2 ] = _mm_extract_epi64(P1, 0 ); tem[3 ] = _mm_extract_epi64(P1, 1 ); tem[4 ] = _mm_extract_epi64(P2, 0 ); gf_mod(res, tem); }
乘方
复用乘法
直接调用gf_mul(),然后一个个相乘,于是有:
1 2 3 4 5 6 7 8 9 void gf_pow_trivial (uint64_t res[5 ], const uint64_t a[5 ], uint64_t n) { uint64_t tem[5 ] = {1 , 0 , 0 , 0 , 0 }; for (uint64_t i = 0 ; i < n; i++) { gf_mul(tem, tem, a); } gf_mod(res, tem); }
快速幂
利用快速幂的思路,本质是对指数进行二进制展开,然后根据展开的结果,不断平方,最后乘到结果上。于是有:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 void gf_pow_fast (uint64_t res[5 ], const uint64_t a[5 ], uint64_t n) { uint64_t tem[5 ] = {1 , 0 , 0 , 0 , 0 }; uint64_t base[5 ]; for (int i = 0 ; i < 5 ; i++) { base[i] = a[i]; } while (n) { if (n & 1 ) { gf_mul(tem, tem, base); } gf_pow2(base, base); n >>= 1 ; } gf_mod(res, tem); }
求逆
拓展欧几里得算法
参考书中 2.3.6 节 的伪代码即可:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 void gf_inv_euclid (uint64_t res[5 ], const uint64_t a[5 ]) { uint64_t u[5 ] = {0 }, v[5 ] = {0 }; for (int i = 0 ; i < 3 ; i++) { u[i] = a[i]; v[i] = F[i]; } uint64_t g1[5 ] = {1 , 0 , 0 , 0 , 0 }; uint64_t g2[5 ] = {0 , 0 , 0 , 0 , 0 }; uint64_t tem[5 ] = {0 }; while (degree(u)) { int d = degree(u) - degree(v); if (d < 0 ) { for (int i = 0 ; i < 5 ; i++) { uint64_t tem = u[i]; u[i] = v[i]; v[i] = tem; } for (int i = 0 ; i < 5 ; i++) { uint64_t tem = g1[i]; g1[i] = g2[i]; g2[i] = tem; } d = -d; } left_shift(tem, v, d); for (int i = 0 ; i < 5 ; i++) { u[i] ^= tem[i]; } left_shift(tem, g2, d); for (int i = 0 ; i < 5 ; i++) { g1[i] ^= tem[i]; } } gf_mod(tem, g1); for (int i = 0 ; i < 5 ; i++) { res[i] = tem[i]; } }
Itoh-Tsujii 算法
论文A fast algorithm for computing multiplicative inverses in GF(2m) using normal bases 提出了基于费马小定理和二进制展开的 Itoh-Tsujii 算法 。
在 F 2 m F_{2^m} F 2 m x 2 m − 1 ≡ 1 m o d f ( x ) x^{2^m-1}\equiv 1\mod f(x) x 2 m − 1 ≡ 1 mod f ( x ) x 2 m − 2 ≡ x − 1 m o d f ( x ) x^{2^m-2}\equiv x^{-1}\mod f(x) x 2 m − 2 ≡ x − 1 mod f ( x ) x 2 m − 2 x^{2^m-2} x 2 m − 2
本实验中 m = 132 m=132 m = 132 2 132 − 2 2^{132-2} 2 132 − 2 gf_pow()。
一种方法是利用平方函数gf_pow2(),因为:
x 2 m − 2 = ( x 2 m − 1 − 1 ) 2 = ( x 2 m − 2 + 2 m − 3 + ⋯ + 1 ) 2 x^{2^m-2}=(x^{2^{m-1}-1})^2=(x^{2^{m-2}+2^{m-3}+\dots+1})^2
x 2 m − 2 = ( x 2 m − 1 − 1 ) 2 = ( x 2 m − 2 + 2 m − 3 + ⋯ + 1 ) 2
指数上是一个等比数列,用类似于快速幂的思想,记 x i = x 2 i + 2 i − 1 + ⋯ + 1 x_i=x^{2^i+2^{i-1}+\dots+1} x i = x 2 i + 2 i − 1 + ⋯ + 1
x i + 1 = x 2 i + 1 + 2 i + ⋯ + 1 = x 2 ∗ ( 2 i + 2 i − 1 + ⋯ + 1 ) + 1 = x i 2 ∗ x x_{i+1}=x^{2^{i+1}+2^i+\dots+1}=x^{2*(2^i+2^{i-1}+\dots+1)+1}=x_i^2*x
x i + 1 = x 2 i + 1 + 2 i + ⋯ + 1 = x 2 ∗ ( 2 i + 2 i − 1 + ⋯ + 1 ) + 1 = x i 2 ∗ x
按以上迭代过程,不难写出代码。
论文中的方法也是通过迭代先计算出 x 2 m − 1 − 1 x^{2^{m-1}-1} x 2 m − 1 − 1 m − 1 m-1 m − 1 ( a 0 a 1 … a k ) 2 (a_0a_1\dots a_k)_2 ( a 0 a 1 … a k ) 2 n i = ( a 0 a 1 … a i ) 2 n_i=(a_0a_1\dots a_i)_2 n i = ( a 0 a 1 … a i ) 2 x 0 = x = x 2 n 0 − 1 x_0=x=x^{2^{n_0}-1} x 0 = x = x 2 n 0 − 1
当 a 1 a_1 a 1 n 1 = 2 n 0 n_1=2n_0 n 1 = 2 n 0
x 0 ∗ x 0 2 n 0 = x 2 n 0 − 1 ∗ x ( 2 n 0 − 1 ) 2 n 0 = x 2 2 n 0 − 1 = x 2 n 1 − 1 x_0*x_0^{2^{n_0}}=x^{2^{n_0}-1}*x^{(2^{n_0}-1)2^{n_0}}=x^{2^{2n_0}-1}=x^{2^{n_1}-1}
x 0 ∗ x 0 2 n 0 = x 2 n 0 − 1 ∗ x ( 2 n 0 − 1 ) 2 n 0 = x 2 2 n 0 − 1 = x 2 n 1 − 1
当 a 2 a_2 a 2 n 1 = 2 n 0 + 1 n_1=2n_0+1 n 1 = 2 n 0 + 1
x ( x 0 x 0 2 n 0 ) 2 = x ( x 2 2 n 0 − 1 ) 2 = x 2 2 n 0 + 1 − 1 = x 2 n 1 − 1 x(x_0x_0^{2^{n_0}})^2=x(x^{2^{2n_0}-1})^2=x^{2^{2n_0+1}-1}=x^{2^{n1}-1}
x ( x 0 x 0 2 n 0 ) 2 = x ( x 2 2 n 0 − 1 ) 2 = x 2 2 n 0 + 1 − 1 = x 2 n 1 − 1
一般地,有迭代过程:
x i + 1 = { x i x i 2 n i , a i + 1 = 0 x ( x i x i 2 n i ) 2 , a i + 1 = 1 x_{i+1}=
\begin{cases}
x_ix_i^{2^{n_i}}&,a_{i+1}=0\\
x(x_ix_i^{2^{n_i}})^2&,a_{i+1}=1
\end{cases}
x i + 1 = { x i x i 2 n i x ( x i x i 2 n i ) 2 , a i + 1 = 0 , a i + 1 = 1
按照这样迭代,即有 x i + 1 = x 2 n i − 1 x_{i+1}=x^{2^{n_i}-1} x i + 1 = x 2 n i − 1 x k + 1 2 x_{k+1}^2 x k + 1 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 void gf_inv_fermat (uint64_t res[5 ], const uint64_t a[5 ]) { uint64_t x_i[5 ]; for (int i = 0 ; i < 5 ; i++) x_i[i] = a[i]; uint64_t n = M - 1 ; int bits = 0 ; while (n) { n >>= 1 ; bits++; } n = M - 1 ; uint64_t mask = 1ULL << (bits - 2 ); int n_i = 1 ; for (int i = 0 ; i < bits - 1 ; i++) { uint64_t tem[5 ] = {0 }; for (int j = 0 ; j < 5 ; j++) tem[j] = x_i[j]; if (n & mask) { for (int j = 0 ; j < n_i; j++) gf_pow2(tem, tem); gf_mul(tem, x_i, tem); gf_pow2(tem, tem); gf_mul(x_i, a, tem); n_i = n_i * 2 + 1 ; } else { for (int j = 0 ; j < n_i; j++) gf_pow2(tem, tem); gf_mul(x_i, x_i, tem); n_i *= 2 ; } mask >>= 1 ; } gf_pow2(res, x_i); }
注意由于指数大小的限制,这里计算 x 2 n i x^{2^{n_i}} x 2 n i gf_pow2()
性能分析
由于影响因素较多,以下运行时间仅提供数量级和大小关系的参考 。
三种乘法函数的比较
为了防止偶然误差的影响,这里用让三种乘法对同一组数据重复运算 10000 次取均值,然后重复该实验 20 次。多次尝试后,结果相差不大,可认为基本排除误差。最终得到三种乘法所需的时间如下表所示:
gf_mul_trivialgf_mul_bitgf_mul_simd
127383ns
995ns
64ns
多次尝试后,结果相差不大,可认为基本排除误差。
三种平方的函数的比较
让三种平方对同一组数据重复运算 10000 次取均值,然后重复该实验 1000 次。最终得到三种平方所需的时间如下表所示:
gf_pow2_bitgf_pow2_mulgf_pow2_simd
1172ns
56ns
37ns
两种求逆的函数的比较
让两种求逆对同一个数据重复运算 10000 次取均值,然后重复该实验 10 次。最终得到两种求逆所需的时间如下表所示:
gf_inv_eculidgf_inv_femart
81236ns
4498ns
写在最后
写完之后在实验平台上提交,也是跑出来 8 个样例 AC 161.686ms 的成绩,狠狠代打拿下第一!(作为参考,助教的时限开到了 30000ms,大多数同学也是 5 位数的水平)
大获全胜.jpg!