算法设计与分析笔记

第一章 基础知识

算法是一个满足下列条件的计算：

• 输入：有满足给定约束条件的输入
• 输出：能够输出满足给定约束条件的结果
• 有穷性：有限步内必须停止
• 确定性：每一步都是严格定义和确定的动作
• 可行性：每一个动作都能够被精确地机械的执行

---

一般用算法的时间复杂度来度量算法的效率。

算法在机器上真正运行的时间取决于硬件性能，所以一般用该算法解决某问题所需的基本运算次数来表示算法的效率，这个次数通常还与问题的规模$n$有关。所以时间复杂度一般都表示为输入规模的函数$T(n)$。

最后，相同规模的数据，也可能因为数据特点的不同，导致不同的基本运算次数。通常，算法的时间复杂度分为最坏情况下的时间复杂度$W(n)$，以及平均情况下的时间复杂度$A(n)$。

$A(n)=\sum_{I\in S}P_I t_I$，其中$S$是规模为$n$的实例集，某个实例$I\in S$的概率为$P_I$，算法对实例$I$所需的基本运算次数是$t_I$。

---

设$f, g$是定义域为自然数集$\N$的函数

1. 若存在正数$c, n_0$使得对于一切$n\geqslant n_0$，有$0\leqslant f(n)\leqslant c\cdot g(n)$成立，则称$f(n)$的渐进的上界是$g(n)$，记作$f(n)=O(g(n))$
2. 若存在正数$c, n_0$使得对于一切$n\geqslant n_0$，有$0\leqslant c\cdot g(n)\leqslant f(n)$成立，则称$f(n)$的渐进的下界是$g(n)$，记作$f(n)=\Omega(g(n))$
3. 若对于任意的正数$c$都存在$n_0$，使得$n\geqslant n_0$时，有$0\leqslant f(n)< c\cdot g(n)$成立，记作$f(n)=o(g(n))$
4. 若对于任意的正数$c$都存在$n_0$，使得$n\geqslant n_0$时，有$0\leqslant c\cdot g(n)< f(n)$成立，记作$f(n)=\omega (g(n))$
5. 若$f(n)=O(g(n))$且$f(n)=\Omega(g(n))$，则$g(n)$称为渐进的紧的界，记为$f(n)=\Theta(g(n))$

---

大$O$记号的运算规则：

• $O(f)+O(g)=O(\max(f, g))$
• $O(f)+O(g)=O(f+g)$
• $O(f)O(g)=O(fg)$
• $O(cf(n))=O(f(n))$，其中$c>0$是一个常数
• $f=O(f)$
• 如果$g(n)=O(f(n))$，则$O(f)+O(g)=O(f)$

---

设$f, g$是定义域为自然数集$\N$的函数

• 如果$\lim_{n\rightarrow \infin}f(n)/g(n)$存在且等于某个常数$c>0$，则$f(n)=\Theta(g(n))$
• 如果$\lim_{n\rightarrow \infin}f(n)/g(n)=0$，则$f(n)=o(g(n))$
• 如果$\lim_{n\rightarrow \infin}f(n)/g(n)=+\infin$，则$f(n)=\omega(g(n))$

---

设函数$f, g, h$的定义域为$\mathbb{N}$，则：

• 若$f=O(g), g=O(h)$，有$f=O(h)$
• 若$f=\Omega(g), g=\Omega(h)$，有$f=\Omega(h)$
• 若$f=\Theta(g), g=\Theta(h)$，有$f=\Theta(h)$

---

多项式函数：$f(n)=a_0+a_1n+\dots+a_dn^d$，其中$a_d\neq 0$。有$f(n)=\Theta(n^d)$

对数函数：对每个$b>1, \alpha>0$，有$\log_b n=o(n^\alpha)$，也即任何幂函数都比对数函数的阶要高。还有$\log_k n=\Theta(\log_l n)$，无论底数如何，对数函数都是同阶的。

指数函数：对每个$r>1$和每个$d>0$，有$n^d=o(r^n)$，也即任何指数函数都比多项式函数增长得快

阶乘函数：由Stirling 公式

$$n!=\sqrt{2\pi n}\left(\frac n e\right)^n\left(1+\Theta\left(\frac 1 n\right)\right)$$

可得$n!=o(n^n), n!=\omega(2^n), \log(n!)=\Theta(n\log n)$

---

调和级数，可以用积分做其渐进的界：

$$\ln (n+1)=1+\int_1^n \frac 1 x dx\geqslant 1+\sum_{k=2}^n \frac 1 k=\sum_{k=1}^n\frac 1 k \geqslant \int_{1}^{n+1} \frac 1 x dx=\ln n$$

所以：

$$\sum_{k=1}^n\frac 1 k=\Theta(\ln n)$$

---

主定理：设$a\geqslant 1, b>1$为常数，$f(n)$为函数，$T(n)$为非负整数，且：

$$T(n)=aT(\frac n b)+f(n)$$

则：

• 若$f(n)=O(n^{\log _ba-\varepsilon}), \varepsilon>0$，那么$T(n)=\Theta(n^{\log_ba})$
• 若$f(n)=\Theta(n^{\log_ba})$，那么$T(n)=\Theta(n^{\log_b a}\log n)$
• 若$f(n)=O(n^{\log _ba+\varepsilon}), \varepsilon>0$，且对于某个常数$c<1$和所有充分大的$n$都有$af(n/b)\leqslant cf(n)$，那么$T(n)=\Theta(f(n))$

第二章 分治算法

1、基本概念

分治算法基本思想是将一个规模为$n$的问题以某种方式分解为$k$个规模较小的子问题，这些子问题非常小以至于能在常数时间内解决，最后将这些子问题的解合并为原问题的解。这三步就是分治算法的三个步骤：

1. 分（Divide）：将大规模问题分割成若干个更小规模的子问题。如果子问题的规模不够小，则再继续划分，如此递归地进行下去。
2. 治（Conquer）：解决这些子问题。
3. 合（Combine）：将这些子问题的解合并为原问题的解。

其中分这个步骤是分治算法基础和关键，一般要遵循两个原则：

• 平衡子问题原则：分割出的若干个子问题，其规模最好大致相当
• 独立子问题原则：分割出的若干个子问题，之间的重叠越少越好，最好是互相独立的

---

一般地，分治算法时间复杂度可以写为以下递推形式：

$$\begin{align*} W(n)=W(|P_1|)+W(|P_2|)+\dots+W(|P_k|)+f(n) \\ W(c)=C \end{align*}$$

其中$|P_i|$是第$i$个子问题的规模，$f(n)$是合并子问题解的时间开销，$C$是直接求解规模为$c$的子问题的时间开销。

---

根据分解出的子问题规模，具体还有以下两种常见的递推形式：

$$\begin{align*} T(n)=\sum_{i=1}^k a_i T(n-i)+f(n) \\ T(n)=aT(n/b)+d(n) \end{align*}$$

例如：

• 汉诺塔问题$T(n)=2T(n-1)+1$
• 二分查找问题$T(n)=T(n/2)+1$
• 归并排序问题$T(n)=2T(n/2)+n$。

对于第一个方程，可以用迭代法、递归树、尝试法求解；对于第二个方程，易看出这是主定理的形式。

当$d(n)$为常数时，由主定理有：

$$T(n)=\begin{cases} \Theta(n^{\log_ba}) & a\neq 1\\ \Theta(\log n) & a=1 \end{cases}$$

当$d(n)=cn$时，分别对应主定理的三种情况：

$$T(n)=\begin{cases} \Theta(n) & a<b\\ \Theta(n\log n) & a=b\\ \Theta(n^{\log_ba}) & a>b \end{cases}$$

2、实例

2.1、逆序对问题

给定一个包含$n$个元素的数组$A$，一个逆序对是一个满足$i<j$且$A[i]>A[j]$的有序对。求逆序对的数量。

• 分：当数组规模为$n>2$时，将数组分为两个规模为$n/2$的子数组
• 治：递归地求解两个子数组的逆序对数量。如果$n=1$，则逆序对数量为 0；如果$n=2$，则逆序对数量为 0 或 1。
• 合：原数组的逆序对数量=两个子数组之间的逆序对数量+跨两个子数组的逆序对数量。

治的时候同时使元素按升序排列，并在并的时候按照升序合并，这样可以使计算跨两个子数组的逆序对的复杂度降为$O(n)$。（可见，这就是归并排序。所以求逆序对可以再归并排序的基础上进行）

---

时间复杂度递推式：

$$\begin{align*} W(n)=2W(n/2)+O(n)\\ W(1)=0, W(2)=1 \end{align*}$$

所以$W(n)=O(n\log n)$

2.2、芯片测试问题

现有$n$个芯片，其中好芯片至少比坏芯片多一片。每次拿两个芯片测试，每个芯片会报告另一个芯片是好或者坏。好芯片的报告总是正确的，坏芯片的报告可能是正确的，也可能是错误的。设计一个算法，使用最少的测试次数找到一个好芯片。

考虑用其他$n-1$个芯片对剩下的芯片 A 进行测试。首先，好芯片的数量至少为$\lfloor\frac{n}{2}\rfloor+1$，这些好芯片对 A 的报告一定是正确的

• A 是好的，则至少有$\lfloor\frac{n}{2}\rfloor$个芯片报告 A 为好
• A 是坏的，则至少有$\lfloor\frac{n}{2}\rfloor+1$个芯片报告 A 为坏

另外，两个芯片都报告对方是好时，两个芯片都好或者都坏。

---

于是可以考虑如下分治策略：

• 分：当$n>3$时，两两一组做测试，互相报告为好的组，任留一片，另一片丢弃；其他情况，两片都丢弃。当$n$为奇数时，最后剩下的一个芯片用其余$n-1$个芯片测试，由上面的结论，可以直接判断出该芯片是好还是坏。如果是好的，算法结束；如果是坏的，直接丢弃。
• 治：$n<=3$时，一次测试即可确定好芯片。
• 合：治的时候，已经得到了

---

下面证明算法正确性。假设$n$为偶数，考虑分的时候，A、B 都好的有$i$组，一好一坏的有$j$组，A、B 都坏的有$k$组。则有：

$$\begin{align*} 2i+2j+2k=n\\ 2i+j>2k+j \end{align*}$$

淘汰后，好芯片数量为$i$，坏芯片数量为$k$，由上面的式子，有$i>k$。所以“好芯片至少比坏芯片多一片”的性质始终保留。$n$为奇数时，通过轮空处理，如果算法没结束，丢弃的一定是坏芯片，性质仍然保留，转化为$n$为偶数的情况。

最终剩余 3 片以内时：

• $n=1, 2$，剩下的芯片一定都是好的
• $n=3$，好芯片至少两片。任取两个芯片，做一次测试，一定可以判断出三个芯片的好坏情况。

---

时间复杂度递推式：

$$\begin{align*} W(n)=W(n/2)+O(n)\\ W(3)=1, W(2)=W(1)=0 \end{align*}$$

最终有$W(n)=O(n)$

2.3、快速排序

给定一个长度为$n$的数组 A，输出排序后的数组。

• 分：当$n$>1 时，选取某个元素$x$为基准，将数组分为两个子数组 A1、A2，使得 A1 中的元素都小于等于$x$，A2 中的元素都大于$x$。接下来递归地对 A1、A2 进行排序。
• 治：当$n<=1$时，数组已排好序。
• 合：合并 A1、x、A2。由于子数组都是排好序的，[A1, x, A2]就是有序的。

---

快速排序的时间复杂度与选择的基准元素有关，划分出的两个子数组的规模直接影响了排序效率。

最坏的情况下，每次一个子数组长度满的，另一个子数组空的：

$$\begin{align*} W(n)=W(n-1)+n-1\\ W(1)=W(0)=0 \end{align*}$$

所以$W(n)=n(n-1)/2$

最好的情况下，每次划分都能均匀划分：

$$\begin{align*} T(n)=2T(n/2)+n-1\\ T(1)=T(0)=0 \end{align*}$$

所以$T(n)=\Theta(n\log n)$

---

考虑计算平均时间复杂度。假设每次选择首元素划分后，首元素位于第$i$个位置（从 1 开始），那么有：

$$T(n)=T(i-1)+T(n-i)+n-1$$

首元素处于每个位置的概率都是$1/n$，所以：

$$\begin{align*} A(n)=\frac 1 n\sum_{i=1}^n[T(i-1)+T(n-i)+n-1]\\ A(1)=A(0)=0 \end{align*}$$

可算出$T(n)=\Theta(n\log n)$

2.4、快速幂

给定整数$a, b$，求$a^b$。

• 分：$b>=2$时，对指数分解。当$b$为偶数时，考虑计算$a^{b/2}$；当$b$为奇数时，考虑计算$a^{(b-1)/2}$
• 治：$b=1$，$a$就是子问题结果
• 和：对子问题结果平方，再视$b$的奇偶性决定是否再乘以$a$

时间复杂度的递推式：

$$\begin{align*} W(n)=W(n/2)+\Theta(1)\\ W(1)=0 \end{align*}$$

可得$W(n)=\Theta(\log n)$

---

利用相同的思想可以得到快速矩阵幂。例如斐波那契数列的计算可以写成矩阵形式：

$$\begin{bmatrix} F_{n+2} & F_{n+1}\\ F_{n+1} & F_n \end{bmatrix}=\begin{bmatrix} F_{n+1} & F_n\\ F_n & F_{n-1} \end{bmatrix}\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^n\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n+1}$$

接下来可以用矩阵快速幂的方法计算。

2.5、选择问题

给定一个长度为$n$的数组 A ，找最大和最小的元素。

• 直接遍历。最坏的时间复杂度为$W(n)=n-1+n-2=n-3$

• 分治算法。两两一组，可以分为$\lfloor n/2\rfloor$组。组内比较大小，得到$\lceil n/2\rceil$个“较小”/“较大”（奇数时为$\lfloor n/2\rfloor+1$）。然后遍历这些“较小”/“较大”，得到最小/最大的元素，还需要比较$2(\lceil n/2\rceil-1)$次。所以最坏时间复杂度为$W(n)=\lfloor n/2\rfloor+2\lceil n/2\rceil-2=\lceil 3n/2\rceil-2$，比直接遍历要好。可以证明，这就是时间复杂度最低的算法。

---

给定一个长度为$n$的数组 A ，找第二大的元素。

• 直接遍历两次。最坏的时间复杂度为$W(n)=n-1+n-2=2n-3$

• 锦标赛算法。每次两两一组比赛，胜者进入下一轮。由于第二大的元素只可能被最大的元素淘汰。所以可以每次做比较时，将被败者元素添加到胜者元素对应的链表上。最后查找最大元素的链表中最大的元素即可。

  最大元素能一直进入下一轮，比较$\lceil \log_2 n\rceil$次，在链表中查找最大元素需要比较$n-1$次，所以最终其链表长度为$\lceil \log_2 n\rceil-1$。每轮比赛每组都淘汰一个元素，最终一共淘汰$n-1$个元素，进行了$n-1$次比较。所以时间复杂度为$W(n)=\lceil \log_2 n\rceil-1+n-1=n+\lceil \log_2 n\rceil-2$。可以证明，这就是时间复杂度最低的算法。

---

给定一个长度为$n$的数组 A ，找第 k 大的元素。这是最一般的选择问题。

• 直接排序后查找。时间复杂度为$O(n\log n)$

• 分治算法。每次选取一个基准元素$m^*$，比其小的划分为一个子数组，比其大的划分为另一个子数组。根据子数组的元素个数，决定进入哪一个子数组进行递归。

  如果选择算法的时间复杂度为$T(n)$，则选择基准元素的复杂度应该为$T(cn)$，其中$c<1$。最坏情况下，每次递归调用都进入规模较大的子数组，解决子问题的时间复杂度应该为$T(dn)$，其中$d>1$。而且要有$c+d<1$，才能使最终复杂度达到$O(n)$。

  考虑五个元素一组，找到每组的中位数，然后找到所有中位数的中位数，作为基准元素。然后将整个数组按下图分为四块：

  

  每列就是刚才的一组，设其是从大到小排序的，所以组的中位数恰好都在第三行。列之间根据中位数大小排序基准元素就在第三行的中间。显然 C 中元素都比$m^*$小，B 中元素都比$m^*$大。需要遍历 A、D 两块来确定其中哪些元素大于/小于$m^*$。这样，得到划分后的子数组。然后递归调用。

  不妨设$n$是 5 的倍数，且$n/5=2r+1$为奇数。有$|A|=|D|=2r, |B|=|C|=3r+2$。最坏的情况下，递归调用进入的子数组规模为$|A|+|D|+|C|=7r+2<0.7n$。

  所以最坏情况下的时间复杂度$W(n)\leqslant W(n/5)+W(7n/10)+tn$。由主定理，有$W(n)=O(n)$。不等号右侧第一项对应调用选择算法查找中位数的中位数，第二项对应递归调用，第三项对应找每组中位数以及处理 A、D 两块的时间。

2.6、多项式在 1 的全体$2n$次方根的值

1 在复数域上开$2n$次方，有$2n$个根$\omega_i=\cos \frac{\pi j}{n}+i\sin \frac{\pi j}{n}$，$i=0, 1, \dots, 2n-1$。给定一个多项式$A(x)=a_0+a_1x+\dots+a_{n-1}x^{n-1}$，求所有$A(\omega_i)$。

• 根据定义，一个个的求。求单个$A(\omega_i)$的时间复杂度为$O(n^2)$，总的时间复杂度为$O(n^3)$

• 迭代法。有迭代式$A_i(x)=a_{n-i}+xA_{i-1}(x), A_1(x)=a_{n-1}$，所以$A_n(x)=A(x)$。
  求单个值的时间复杂度为$O(n)$，总的时间复杂度为$O(n^2)$

• 分治算法。不妨设$n=2r$，考虑多项式$A_0(x)=a_0+a_2 x+\cdots+a_{2r}x, A_1(x)=a_1+a_3 x+\cdots+a_{2r-1}(x)$。则$A(x)=A_0(x^2)+xA_1(x^2)$。所以可以递归地求解。

  有$\omega_i^2=\omega_{(2i)\%(2n)}$。所以$A(\omega_i)=A_0(\omega_{(2i)\%(2n)})+\omega_i A_1(\omega_{(2i)\%(2n)}), \forall j$，也即原问题可以划分为两个规模减半的子问题。所以整个问题时间复杂度为$T(n)=2T(n/2)+O(n)$，由主定理有$T(n)=O(n\log n)$。

2.7、平面点集凸包问题

给定一个平面上的点集，找到包含所有点的最小凸多边形。

考虑分治算法。首先找到纵坐标最大和最小的两个点，用它们之间的连线$d$将点集划分为左右两部分。然后找到距离$d$最远的点$P$，这个点与$d$的两个端点连线分别为$a, b$，则$a, b, d$构成一个三角形。三角形内的点直接删去，a 及其外侧的点构成一个新的点集，b 及其外侧的点构成另一个新的点集。递归地求解。

初始划分的时间复杂度为$O(n)$。每次根据$d$找到$P$的时间复杂度为$O(n)$，然后划分子问题的时间复杂度为$O(n)$。最坏的情况下，每次划分出的子问题规模为$n-1$，时间复杂度为$W(n)=W(n-1)+O(n)$，可得$W(n)=O(n^2)$。所以总的时间复杂度为$O(n^2)$。

3、分治算法的改进

3.1、减少子问题个数

考虑分治算法时间复杂度递推式：

$$W(n)=aW(n/b)+d(n)$$

当$a>b$，$d(n)$不大时，由主定理，有$W(n)=\Theta(n^{\log_ba})$，此时减少$a$可以降低$W(n)$的阶。

利用子问题之间的依赖关系，使得某些子问题的解可以通过组合其他子问题的解得到。这样，可以减少子问题的个数，降低时间复杂度。

---

考虑两个$n$位的二进制数$X, Y$相乘。直接相乘，需要$O(n^2)$次乘法运算。

将每个数分为两部分$X=X_1\cdot 2^{n/2}+X_0, Y=Y_1\cdot 2^{n/2}+Y_0$，则其乘积可以写为：

$$X\cdot Y=(X_1\cdot 2^{n/2}+X_0)(Y_1\cdot 2^{n/2}+Y_0)=X_1Y_1\cdot 2^n+(X_1Y_0+X_0Y_1)\cdot 2^{n/2}+X_0Y_0$$

时间复杂度$W(n)=4W(n/2)+O(n)$，由主定理，有$W(n)=O(n^{\log_2 4})=O(n^2)$。

寻找子问题之间的依赖关系，可以发现：

$$X_1Y_0+X_0Y_1=(X_1+X_0)(Y_1+Y_0)-X_1Y_1-X_0Y_0$$

所以仅需要三次乘法运算，就可以得到$X\cdot Y$。时间复杂度降为$W(n)=3W(n/2)+O(n)$，由主定理，有$W(n)=O(n^{\log_2 3})=O(n^{1.59})$。

---

Strassen 矩阵乘法，也用了类似的思想。将两个矩阵相乘，考虑将每个矩阵分为四个子矩阵，可以得到：

$$\begin{bmatrix} A_{11} & A_{12}\\ A_{21} & A_{22} \end{bmatrix}\begin{bmatrix} B_{11} & B_{12}\\ B_{21} & B_{22} \end{bmatrix}= \begin{bmatrix} C_{11} & C_{12}\\ C_{21} & C_{22} \end{bmatrix}$$

如果只是普通的分块计算：

$$\begin{align*} C_{11}=A_{11}B_{11}+A_{12}B_{21}\\ C_{12}=A_{11}B_{12}+A_{12}B_{22}\\ C_{21}=A_{21}B_{11}+A_{22}B_{21}\\ C_{22}=A_{21}B_{12}+A_{22}B_{22} \end{align*}$$

时间复杂度为$W(n)=8W(n/2)+O(n^2)$，由主定理，仍然是$W(n)=O(n^3)$。

考虑这样计算：

$$\begin{align*} M_1=A_{11}(B_{12}-B_{22})\\ M_2=(A_{11}+A_{12})B_{22}\\ M_3=(A_{21}+A_{22})B_{11}\\ M_4=A_{22}(B_{21}-B_{11})\\ M_5=(A_{11}+A_{22})(B_{11}+B_{22})\\ M_6=(A_{12}-A_{22})(B_{21}+B_{22})\\ M_7=(A_{11}-A_{21})(B_{11}+B_{12}) \end{align*}$$

则：

$$\begin{align*} C_{11}=M_5+M_4-M_2+M_6\\ C_{12}=M_1+M_2\\ C_{21}=M_3+M_4\\ C_{22}=M_5+M_1-M_3-M_7 \end{align*}$$

所以时间复杂度为$W(n)=7W(n/2)+O(n^2)$，由主定理，有$W(n)=O(n^{\log_2 7})=O(n^{2.81})$。

目前最好的算法是 Coppersmith-Winograd 算法，时间复杂度为$O(n^{2.376})$。

3.2、增加预处理

用平面最邻近点对问题说明：给定一个平面点集，找到之间距离最短的一对点。

朴素方法，两两枚举。共有$C_n^2$对点，时间复杂度为$O(n^2)$。

分治方法，将点集分为两部分，分别求解，然后考虑跨两部分的最邻近点对，一共三部分。

• 分割考虑做中垂线（也即按照 x 坐标分割），分为大小相近的两部分。一开始按 x 坐标进行排序$O(n\log n)$，后续的分割只需要$O(n)$时间，总共是$O(n\log n)$
• 对于找跨两部分的点对，设两部分中最邻近点对的距离分别是$\delta_0, \delta_1$，则只需考虑中垂线两边$\delta=\min(\delta_0, \delta_1)$之内的点。假设中垂线左侧，距中垂线距离小于$\delta$的一个点$(x_1, y_1)$，只需要考虑中垂线右侧，同样到中垂线距离小于$\delta$，且纵坐标范围是$[y_1-\delta, y_1+\delta]$的点。可以证明，这样的点至多有 6 个。找到点$(x_1, y_1)$需要$O(n)$时间，在 y 坐标有序的情况下，找到另一侧满足要求的点需要$O(n)$时间，检查是$O(1)$的，总共也是$O(n\log n)$的（按 y 进行排序）。

所以总的时间复杂度递推式为$W(n)=2W(n/2)+O(n\log n)$，用递归树可解得$W(n)=O(n\log^2 n)$

---

上面的分治方法中，每次递归都要调用一次排序（对 y 进行排序），这是因为分割的时候是对 x 进行排序，不能保证顶点数组中 y 的坐标也是有序的。有没有可能，分割的时候，同时能得到 x 的有序性和 y 的有序性，且还能够正常将每个点的 x 和 y 对应起来？

考虑预处理，一开始按 y 也进行排序，不过要带上额外信息，用于确定其属于那个点。

用 C++数据结构来说明：一开始有顶点坐标数组vector<pair<float, float>> points。创建pair<float, int> x，其中第一个元素是某个顶点的 x 坐标，第二个元素是顶点 ID（可以取在原顶点数组中的下标）。然后按 x 坐标排序，得到有序的vector<pair<float, int>>。再创建pair<float, int>，其中第一个元素是 y 坐标，第二个元素是顶点 ID 。按 y 坐标排序，得到有序的vector<pair<float, int>>。

然后进行分割。可以在$O(n)$的时间内得到vector<pair<float, int>> x_1, x_2。根据顶点 ID，扫描vector<pair<float, int>> y，顶点 ID 相同，说明是同一个点的 y 坐标，划分到对应的部分。可以在$O(n)$内得到vector<pair<float, int>> y_1, y_2，且仍然是有序的。

这样时间复杂度递推式为$W(n)=2W(n/2)+O(n)$，由主定理，有$W(n)=O(n\log n)$。

第三章 动态规划

1、基本概念

多阶段决策问题是指，求解的问题求解的问题可以划分为一系列相互联系的阶段，在每个阶段都需要作出决策，且一个阶段决策的选择会影响下一个阶段的决策，从而影响整个过程的活动路线，求解的目标是选择各个阶段的决策使整个过程达到最优。

动态规划（Dynamic Programming）就是一种在研究多阶段决策问题时提出的一种解方法，其基本思想是把多阶段过程转化为一系列单阶段问题，然后逐个求解。动态规划常常用于求解以时间划分阶段的动态过程的优化问题，对于一些与时间无关的静态规划，也可以以人为引入时间因素，然后同样适用动态规划地方法求解。

---

• 阶段：利用动态规划求解问题，需要将问题恰当地划分为若干个相互联系的阶段
• 状态：每个阶段开始时，问题或者系统所处的客观状况。状态既是某个阶段的某个起点，也是前一个阶段的某个终点，一个阶段可以有若干种可能的状态。
• 策略：每个阶段都需要作出决策，决策使得系统从一个状态转移到另一个状态。各个阶段的决策构成一个决策序列，这个序列就称之为一个策略。从某个阶段开始到终止阶段的过程称为一个子过程，对应的策略称为一个子策略。

状态的无后效性是指，某个阶段的状态给定之后，则该阶段之后的过程的发展不受该阶段以前各段状态的影响，也就是说状态具有马尔可夫性。适用于动态规划求解的问题，其中各个状态必须具有无后效性。

---

动态规划的实质是分治+减少冗余计算。

动态规划也是将原问题分解为若干个子问题，先求解子问题，然后根据子问题的解得到原问题的解。

与分治不同的是，动态规划中子问题往往不是相互独立的，会出现相同的子问题。如果使用分治方法求解，会有很多重复计算。动态规划用一个表来保存子问题的解，自底向上计算，最终求出原问题的解。

---

利用动态规划求解问题的一般步骤：

1. 找出最优解的性质，并刻画其结构特征
2. 递归地定义最优值，也即写出动态规划方程（状态转移方程）
3. 自底向上计算最优值
4. 根据计算最优值时得到的信息，构造最优解（可选）

2、Bellman 最优性原理

如果某个问题的最优策略的子策略总是最优的，则称该问题满足 Bellman 最优性原理。对于满足 Bellman 最优性原理的问题，如果其某个策略的子策略不是最优的，则该策略也不是最优的。

---

有向带权图$G$中，从顶点$v_i$到$v_j$的最短路径问题是满足最优性原理的。

证：假设该问题不满足最优性原理，则存在一条$v_i$到$v_j$的最短路径$v_i\rightarrow u \rightarrow w \rightarrow v_j$，其中的子路径$u \rightarrow w\rightarrow v_j$不是$u$到$v_j$的最短路径。

假设$u$到$v_j$的最短路径是$u\rightarrow w'\rightarrow v_j$，则路径$v_i\rightarrow u \rightarrow w' \rightarrow v_j$比原来的路径更短，与原来的路径是最短路径的假设矛盾。

由反证法可知，从顶点$v_i$到$v_j$的最短路径问题满足最优性原理。

---

无向无权图$G$中，从顶点$q$到$t$的最长路径问题不满足最优性原理。设$G$是一个环$q\leftrightarrow r \leftrightarrow s \leftrightarrow t \leftrightarrow q$。

$q$到$t$的最长路径是$q\rightarrow r\rightarrow t$。但是$q$到$r$的最长路径是$q\rightarrow s\rightarrow t\rightarrow r$；$r$到$t$的最长路径是$r\rightarrow q\rightarrow s\rightarrow t$。两个子问题的最优策略组合起来，不是整个问题的最优策略。说明该问题不满足最优性原理。

---

动态规划方法对问题的有效性，取决于问题本身是否满足：

• 最优子结构：也称为优化原则，是指一个最优决策序列的任何子序列本身一定是相对于子序列初始和结束状态最优的决策序列。
• 重叠子问题：递归求解时，会需要反复求解相同的子问题。动态规划方法会将子问题的解保存在一个表中，能够避免重复计算。

---

动态规划算法设计的要点：

1. 问题要求什么？约束条件是什么？
2. 如何划分子问题？
3. 原问题的最优值与子问题的最优值之间的关系是什么？（状态转移方程）
4. 是否满足最优子结构？
5. 最小的子问题是什么？其解如何计算？（边界条件）

3、实例

3.1、多起点多终点的最短路径问题

给定一个有向带权图$G$，起点集$\{S_1, S_2, \dots, S_n\}$，终点集$\{T_1, T_2, \dots, T_m\}$，求出起点在起点集，终点在终点集的最短路径。

---

蛮力算法，穷举每一条可能的路径。假定起点到终点的（平均）要经过$k$条边，则时间复杂度达到$O(n2^k)$。

动态规划算法，考虑从终点开始，逐步前推。先求出起点集为$\{C_i\}$，终点为$\{T_j\}$的最短路径$F(C_i)=\min_{j}\{C_iT_j\}$。然后求出起点集为$\{B_k\}$，终点为$\{T_j\}$的最短路径$F(B_k)=\min_{j}\{B_kC_j+F(C_j)\}$。依次类推，最终有$F(S_l)=\min_{m}\{S_lA_m+F(A_m)\}$。最小的$F(S_l)$对应的路径即为所求。

---

能使用动态规划算法，是因为满足最优子结构。即全局最短路径的子路径，也一定是相对这个子路径起点和终点的最短路径。

3.2、矩阵链相乘

给定矩阵序列$\boldsymbol{A}_1, \boldsymbol{A}_2, \dots, \boldsymbol{A}_n$，其中$\boldsymbol{A}_i$的规模为$P_{i-1}\times P_i$，求出最优的矩阵相乘顺序，使得计算元素相乘的总次数最少。（矩阵的行数和列数限定整个序列的顺序不变，利用结合律，通过加括号的方法，得到不同的计算次数）

---

蛮力算法，考虑穷举每一种可能的加括号方式。加完括号的序列可以写成一个二叉树，树的每个叶子节点都对应一个矩阵，每个子树对应着一个一对括号。由叶子节点开始，逐步向上计算，最终得到根节点对应的矩阵。根节点矩阵就对应着答案，整个过程就对应着计算的过程。

设$n$个叶子节点的二叉树有$x_n$种，有递推公式：

$$x_{n+1}=\sum_{i=1}^n x_i x_{n+1-i}, x_1=1, x_2=1$$

也即$i$个叶子结点的二叉树和$n+1-i$个叶子节点的二叉树，分别作为根节点的两个子树，得到$n+1$个叶子节点的二叉树。这个形式与卡特兰数（Catalan Number）的定义本质上相同：

$$C_{n}=\sum_{i=0}^{n-1}C_{i}C_{n-1-i}, C_0=1, C_1=1$$

也即有$x_{n+1}=C_n$。

所以对于长度为$n+1$的矩阵序列，其可能的运算顺序有$C_n$种，利用 Stirling 公式，可得穷举的时间复杂度为：

$$W(n)=\Omega(C_n)=\Omega(\frac{1}{n+1}\frac{(2n)!}{n!n!})=\Omega\left(\frac{4^n}{n^{3/2}}\right)$$

这是一个指数级别的时间复杂度。

---

动态规划算法。考虑某个矩阵链$\boldsymbol{A}_i\boldsymbol{A}_{i+1}\dots\boldsymbol{A}_j$，记其最少运算次数为$m[i, j]$。假设其最后一次相乘是在$k$处（运算树的根节点对应的位置），也即最后相当于是$\boldsymbol{A}_i\boldsymbol{A}_{i+1}\dots\boldsymbol{A}_k$和$\boldsymbol{A}_{k+1}\boldsymbol{A}_{k+2}\dots\boldsymbol{A}_j$相乘。假设两个子部分都采用了最优的运算次序，则这种情况下的乘法次数应该是：

$$m[i, k]+m[k+1, j]+P_{i-1}P_kP_j$$

所以每一个问题，可以遍历最后一次乘法出现的位置，写出递推式如下：

$$m[i, j]=\begin{cases} 0, & i=j\\ \min_{i\leqslant k<j}\{m[i, k]+m[k+1, j]+P_{i-1}P_kP_j\}, & i<j \end{cases}$$

该问题是满足最优子结构的。

---

利用数学归纳法，如果不做任何其他处理，可以证明上面动态规划方法的时间复杂度$T(n)\geqslant 2^{n-1}$，还是指数级别！

这是因为，每次遇到$m[i, j]$，我们都当做一个子问题重新计算。实际上，可以发现我们进行了大量的重复计算，有很多子问题是重复的。所以，我们可以将子问题的解保存在一个表（备忘录）中，之后再遇到的时候，直接查表即可。

追踪解时，只需记录下每次最终选取的$k$值即可。

记忆化之后，时间复杂度降低到$O(n^3)$。

3.3、投资问题

有$m$元钱，$n$个投资项目，$f_i(x)$是将$x$元投入第$i$个项目的收益。求出使得总收益最大的投资方案。

---

记$F_k(x)$是将$x$元投入前$k$个项目的最大收益。考虑将一部分前投入前$k-1$个项目，剩下的前投给第$k$个项目，则有递推式：

$$F_k(x)=\max_{0\leqslant y\leqslant x}\{F_{k-1}(x-y)+f_k(y)\}$$

时间复杂度为$O(nm^2)$。

3.4、一般背包问题

假设将$n$种物品（每种物品有无数个）放入一个背包，第$i$个物品的重量为$w_i$，价值为$v_i$，背包的重量限制为$b$。求出使得背包中物品的总价值最大的方案。

---

记只考虑前$k$种物品，总重不超过$y$时的最大价值为$F_k(y)$。每次考虑装至少装入一个物品$k$还是不装，容易写出递推式：

$$F_k(y)=\max\{F_{k-1}(y), F_{k}(y-w_k)+v_k\}$$

追踪解，只需同时记录一个$i_k(y)$，表示计算$F_k(y)$时，最终方案中装入物品的最大标号。具体来说，其更新公式如下：

$$i_k(y)=\begin{cases} i_{k-1}(y), & F_{k-1}(y)> F_k(y-w_k)+v_k\\ k, & F_{k-1}(y)\leqslant F_k(y-w_k)+v_k \end{cases}$$

$F_n(b)$即为最终的解。$x=i_n(b)$是最后一个装入的物品，$i_n(b-w_x)$是倒数第二个装入的物品，以此类推。

时间复杂度为$O(nb)$。

3.5、最长公共子序列问题

设两个序列$X=\{x_1, x_2, \dots, x_m\}$和$Z=\{z_1, z_2, \dots, z_n\}$。如果存在$j_1<j_2<\dots<j_n$，使得$z_i=x_{j_i}, \forall i=1, 2, \dots, n$，则称$Z$是$X$的一个子序列。如果$Z$同时是$X$和$Y$的子序列，就称它是$X$和$Y$的公共子序列（LCS）。

给定两个序列$X$和$Y$，求出它们的最长公共子序列。

---

蛮力算法。依次检查$X$的所有子序列是否在$Y$中。子序列有$2^{|X|}$种，检查一个子序列是否存在另一个序列中，需要$|Y|$的时间。假定$m=|X|\leqslant |Y|=n$，则时间复杂度可写为$O(n 2^m)$

---

动态规划算法。记考虑$X$的前$i$个元素，以及$Y$的前$j$个元素时的 LCS 长度为$C[i, j]$。可以想到，如果$x_i=y_j$，则可以添加到目前 LCS 的末尾，使 LCS 长度增加。所以有递推公式如下：

$$C[i, j]=\begin{cases} C[i-1, j-1]+1, & x_i=y_j\\ \max\{C[i-1, j], C[i, j-1]\}, & x_i\neq x_j \end{cases}$$

追踪解，根据上面三种情况反向追踪即可。

总的时间复杂度为$O(mn)$。

3.6、黑白图像存储问题

设图像像素序列为$\{p_1, p_2, \dots, p_n\}$，其中每个像素点$p_i$都是一个 0~255 的灰度值，需要 8 位来存储。

考虑对像素点序列进行分段$S_1, S_2, \dots, S_m$，段$S_i$有$l[i]$个像素（$l[i]-1\leqslant 255$），每个像素都用$b[i]$位来存储，则总的存储位数为$(l[i]b[i]+8+3)\cdot m$。其中$b_i$满足：

$$b[i]=\left\lceil\log_2\left(\max_{p_j\in S_i}p_j+1\right)\right\rceil$$

求出最佳分段方案，使得总的存储位数最少。

---

动态规划算法。记$S[i]$是前$i$个像素的采用最佳分段方案所需的存储位数，考虑最后一个段$S_m$如何划分，则有：

$$S[i]=\min_{1\leqslant j\leqslant \min\{i, 256\}}\{S[i-j]+j\cdot b[m]+11\}, b_m=\left\lceil\log_2\left(\max_{p_j\in S_m}p_j+1\right)\right\rceil$$

追踪解只需要记录每次最终选择的$j$值，这就是每段的长度。

总的时间复杂度为$O(n)$。

3.7、最大子串和问题

给定$n$个数的序列（可能存在负数）$A=\{a_1, a_2, \dots, a_n\}$，求出一个连续子串，使得子串的和最大。

---

蛮力算法。暴力枚举每一个子串，使用前缀和数组的情况下，时间复杂度为$O(n^2)$。

---

分治算法。考虑前半段中的最大子串和以及后半段的最大子串和，以及跨越两个段的最大子串和。跨越两个段的情况，可以从中间往两边拓展，可在$O(n)$时间内求解。

所以时间复杂度$T(n)=2T(n/2)+O(n)$，由主定理，有$T(n)=O(n\log n)$。

---

动态规划算法。记$S[i]$是以$a_i$结尾的最大子串和，容易得到递推公式：

$$S[i]=\max\{S[i-1]+a_i, a_i\}$$

时间复杂度为$O(n)$。

3.8、最优二叉搜索树问题

假设有形如下图的二叉搜索树：

其中圆形节点表示是实际数据，方形节点是虚拟节点，是不在二叉搜索树中的数据最终落在的位置。每个节点都有一个概率，表示是搜索中最终节点的概率。

设实际数据集为$\{x_1, x_2, \dots, x_n\}$，求出一种最优的二叉搜索树，使得搜索的期望比较次数最小。

---

动态规划算法。考虑某段数据$\{x_i, x_{i+1}, \dots, x_j\}$，从中选择$x_k$作为根。记$m[i, j]$是这段数据的最优二叉搜索树的期望比较次数，$w[i, j]$为这段数据（包括实际数据以及虚拟节点）的概率和。提出根节点之后，到左右子树的比较次数都增加了 1。终点落在根节点上，需要一次比较。所以有：

$$m[i, j]=\min_{i\leqslant k\leqslant j}\{m[i, k-1]+1\cdot w[i, k-1] + m[k+1, j]+1\cdot w[k+1, j] + 1\cdot p_k\}$$

化简后，有：

$$m[i, j]=\min_{i\leqslant k\leqslant j}\{m[i, k-1]+m[k+1, j]+w[i, j]\}$$

总的时间复杂度为$O(n^3)$。

第四章 贪心算法

1、基本概念

贪心法的基本思想是：在对问题求解时，总是做出在当前看来是最好的选择。也即，不从整体最优上加以考虑，只做局部最优解。显然，这样做并不一定能得到全局最优解。

贪心选择性质是指，一个问题的整体最优解可以通过一系列局部最优的选择得到。要想使用贪心算法得到最优解，必须证明问题具有贪心选择性质。

之前已经提到了最优子结构，一个问题拥有最优子结构是能够用动态规划算法以及贪心算法求解的关键特征。并不是所有具有最优子结构的问题都能够使用贪心算法求解，但是往往可以利用其来证明贪心选择性质。

2、数学归纳法

证明贪心选择性质时，常常用到数学归纳法。数学归纳法适合证明涉及自然数的命题$P(n)$。

2.1、第一数学归纳法

归纳基础：证明$P(1)$成立（或者$P(0)$成立）。
归纳步骤：假设对任意自然数$k$，$P(k)$成立，证明$P(k+1)$成立。

2.2、第二数学归纳法

归纳基础：证明$P(1), P(2), \dots, P(m)$成立。
归纳步骤：假设对任意自然数$k$，$P(1), P(2), \dots, P(k)$成立，证明$P(k+1)$成立。

3、实例

3.1、活动选择问题

设有$n$个活动，活动$i$的开始时间和结束时间分别为$s_i$和$f_i$。如果活动$i$和活动$j$满足$s_i \geqslant f_j$或者$s_j \geqslant f_i$，则称活动$i$和活动$j$是相容的，求出最大的两两相容的活动集合。

---

贪心策略 1：总是选择开始最早的活动。这样的话，如果某个活动持续非常久，会挤占掉其他活动，可能不如选稍晚一些开始，但很快结束的活动。

贪心策略 2：总是选持续时间最短的活动。这样的话，如果持续时间最短的活动开始的很晚，可能会错过很多活动。

贪心策略 3：总是选择结束时间最早的活动。先按照结束时间排序，然后扫描一遍，选出相容的活动。时间主要消耗在排序上，复杂度为$O(n\log n)$。

---

接下来证明贪心选择性质，下面的贪心策略代指贪心策略 3。假设活动集已按照结束时间升序排列，下面提及的序号都是排序后的序号。

命题：按照贪心策略已经选择了$k$项活动$i_1=1, i_2, \dots, i_k$，存在某个最优解$A$包含活动$i_1=1, i_2, \dots, i_k$。

归纳基础：证明$k=1$时成立，也即证明最优解包含$i_1=1$。反证法，假设最优解中不包含$i_1=1$。任取一个最优解$A$，将其中活动也按结束时间升序排列。由于活动 1 是结束时间最早的活动，一定有$f_1\leqslant f_j$。用活动 1 替换掉活动$j$，得到一个新的解$A'$，对后续活动没有影响，也是一个最优解。这与假设矛盾，所以最优解中一定包含活动 1。

归纳步骤：假设对于$k$，原命题成立，也即此时最优解$A$包含$i_1=1, i_2, \dots, i_k$。$A$的剩余部分$B$来自于集合$S'=\{i| i\in S, s_i \geqslant f_{i_k}\}$。由反证法易得，$B$一定是$S'$的最优解。考虑活动集为$S'$的新问题，由归纳假设，$S'$的$B'$一定包含$S'$中结束时间最早的活动。由$\{i_1, i_2, \dots, i_k\}\cup B'=\{i_1, i_2, \dots, i_k, i_{k+1}\} \cup (B'-\{i_{k+1})\})$是最优解，可得最优解包含$i_1, i_2, \dots, i_k, i_{k+1}$。所以原命题对于$k+1$也成立。

第六章 线性规划

1、基本概念

1.1、一般形式

线性规划问题的一般形式如下：

$$\begin{align*} \min(\max) z=\sum_{j=1}^n c_jx_j\\ \text{s.t.} \sum_{j=1}^n a_{ij}x_j \leqslant(=, \geqslant)b_i, & i=1, 2, \dots, m\\ x_j\geqslant 0,& j\in J\subseteq \{1, 2, \dots, n\}\\ x_j, &j\in \{1, 2, \dots, n\}-J \end{align*}$$

这四行从上到下依次代表：目标函数，约束条件，非负约束条件，自由变量。

---

可行解：满足约束条件和非负条件的变量
可行域：所有可行解的集合
最优解：在可行域中，目标函数取得最小（或最大）值的解
最优值：最优解对应的目标函数值

在高中已经学习过了二维线性规划的图解法，可行域由多条代表约束条件的直线围城，是一个凸多边形（可能无界，也可能是空集）。如果有最优解，一定在凸多边形的顶点取到。解的情况有四种：

• 有唯一最优解
• 有无穷多个最优解
• 有可行解，但无最优解
• 无可行解，也无最优解

推广到一般的$n$维线性规划也是如此。

1.2、标准形

一般线性规划问题，总是可以写成标准形：

$$\begin{align*} \min z=\sum_{j=1}^n c_jx_j\\ \text{s.t.} \sum_{j=1}^n a_{ij}x_j=b_i, & i=1, 2, \dots, m\\ x_j\geqslant 0,& j=1, 2, \dots, n \end{align*}$$

将$\max$改$\min$，或者不等号变号比较简单，不再赘述。对于不等式约束条件，可以通过引入松弛变量/剩余变量，将其转化为等式约束条件：

$$\begin{align*} \sum_{j=1}^n a_{ij}x_j\leqslant b_i \Rightarrow \sum_{j=1}^n a_{ij}x_j+y_i=b_i, y_i\geqslant 0 \\ \sum_{j=1}^n a_{ij}x_j\geqslant b_i \Rightarrow \sum_{j=1}^n a_{ij}x_j-y_i=b_i, y_i\geqslant 0 \end{align*}$$

其中第一行引入的变量称为松弛变量，第二行引入的变量称为剩余变量。

对于自由变量：

$$x_j\in R\Rightarrow x_j=x_j'-x_j'', x_j'\geqslant 0, x_j''\geqslant 0$$

1.3、矩阵形式

标准形可以写为矩阵形式。其中目标函数可写为：

$$\min z=\boldsymbol{c}^T\boldsymbol{x}=\begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{bmatrix}^T \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix}$$

约束条件可写为：

$$\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix}=\begin{bmatrix} \boldsymbol{P}_1 & \boldsymbol{P}_2 & \dots & \boldsymbol{P}_n \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix}=\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}$$

2、标准形的解

2.1、一些定义

设$\boldsymbol{A}$的秩为$r$，$\boldsymbol{A}$的$m$个线性无关的列向量称为标准型的基。

给定标准形的一组基$\boldsymbol{B}=\{\boldsymbol{P}_{i_1}, \boldsymbol{P}_{i_2}, \dots, \boldsymbol{P}_{i_m}\}$，对应变量$x_{i_1}, x_{i_2}, \dots, x_{i_m}$称为基变量，其余变量称为非基变量。

基变量构成的向量记为$\boldsymbol{x}_B$，非基变量构成的向量记为$\boldsymbol{x}_N$。令$\boldsymbol{x}_N=\boldsymbol{0}$，则等式约束变为$\boldsymbol{B}\boldsymbol{x}_B=\boldsymbol{b}$，解得$\boldsymbol{x}_B=\boldsymbol{B}^{-1}\boldsymbol{b}$。将$\boldsymbol{x}_B$和$\boldsymbol{x}_N$重新组装为$\boldsymbol{x}$，这个$\boldsymbol{x}$显然满足等式约束，且非基变量全为 0，称其是关于基$\boldsymbol{B}$的基本解（系数矩阵满秩，所以基本解是唯一的）。如果$\boldsymbol{x}$是基本解，且同时还满足非负约束$x_i\geqslant 0, \forall i$，则称其为基本可行解，对应的基称为一个可行基。

2.2、基本可行解的性质

引理：$\boldsymbol{Ax}=\boldsymbol{b}$的解$\boldsymbol{\alpha}$是基本解当且仅当$\boldsymbol{\alpha}$的非零分量对应的列向量线性无关。

必要性，由基本解的定义立得。

充分性，设$\boldsymbol{\alpha}$非零分量对应的列向量为$\boldsymbol{P}_{j_1}, \boldsymbol{P}_{j_2}, \dots, \boldsymbol{P}_{j_r}$，它们是线性无关的。由于$\boldsymbol{A}$的秩为$m$，必然存在其他$m-r$个列向量$\boldsymbol{P}_{j_{r+1}}, \boldsymbol{P}_{j_{r+2}}, \dots, \boldsymbol{P}_{j_m}$，这一共$m$个列向量线性无关，是$\boldsymbol{A}$的基$\boldsymbol{B}$。则$\boldsymbol{\alpha}$也是方程$\boldsymbol{B}\boldsymbol{x}_B=\boldsymbol{b}$的解，由解的唯一性，$\boldsymbol{\alpha}$就是基本解。

---

定理 1：若标准形有可行解，则必有基本可行解。

证明：设$\boldsymbol{\alpha}$是一个可行解。设其非零分量为$\alpha_1, \alpha_2, \dots, \alpha_r$，对应的列向量为$\boldsymbol{P}_{j_1}, \boldsymbol{P}_{j_2}, \dots, \boldsymbol{P}_{j_r}$。由引理，若这$r$个列向量线性无关，所以$\boldsymbol{\alpha}$是基本解。

若不然，由线性无关，存在不全为 0 的$\lambda_1, \lambda_2, \dots, \lambda_r$，使得$\sum_{i=1}^r \lambda_i\boldsymbol{P}_{j_i}=\boldsymbol{0}$。取$\lambda_{r+1}=\lambda_{r+2}=\dots=\lambda_n=0$，则有$\sum_{i=1}^n \lambda_i\boldsymbol{P}_{j_i}=\boldsymbol{0}$。于是，对任意的$\delta$，有：

$$\sum_{i=1}^n (\alpha_i+\delta \lambda_i)\boldsymbol{P}_{j_i}=\sum_{i=1}^n \alpha_i\boldsymbol{P}_{j_i}+\delta\sum_{i=1}^n \lambda_i\boldsymbol{P}_{j_i}=\boldsymbol{b}$$

如果想让$\boldsymbol{\alpha}+\delta \boldsymbol{\lambda}$成为一个可行解，则$\alpha_i+\delta \lambda_i\geqslant 0, \forall i$

• $\lambda_i=0$时，恒成立
• $\lambda_i>0$时，则要有$\delta \geqslant -\frac{\alpha_i}{\lambda_i}$；当$\lambda_j<0$时，要有$\delta \leqslant -\frac{\alpha_i}{\lambda_i}$。设$k=\arg\min_{i, \lambda_i\neq 0}\{|\frac{\alpha_i}{\lambda_i}|\}$，则取$\delta^*= -\frac{\alpha_k}{\lambda_k}$。显然$\boldsymbol{\beta}=\boldsymbol{\alpha}+\delta^*\boldsymbol{\lambda}$也是一个可行解，而且比$\boldsymbol{\alpha}$少一个非零分量（$\alpha_k+\delta^*\lambda_k=0$）。重复上述过程至多$r$次，就得到了一个基本可行解。

综上，证毕。

---

定理 2：若标准形有最优解，则必定存在一个基本可行解是最优解。

证明：只需在定理 1 的基础上，证明$\boldsymbol{\alpha}$是最优解时，$\boldsymbol{\beta}$也是最优解。

设$\boldsymbol{\alpha}$，显然其也是可行解。对于其任意零分量$\alpha_i$，一定有$\lambda_i=0$，所以对于任意$\delta$，有$\alpha_i\pm \delta \lambda_i\geqslant 0$；对于任意非零分量$\alpha_i$，有$\lambda_i\neq 0$，取一个足够小的$\delta>0$，使仍然有$\alpha_i\pm \delta \lambda_i\geqslant 0$，且等式约束也满足。所以$\boldsymbol{\alpha}\pm\delta \boldsymbol{\lambda}$也是一个可行解。由$\boldsymbol{\alpha}$是最优解，于是有：

$$\sum_{i=1}^n c_i\alpha_i\leqslant \sum_{i=1}^n c_i(\alpha_i\pm \delta \lambda_i)=\sum_{i=1}^n c_i\alpha_i\pm \delta \sum_{i=1}^n c_i\lambda_i$$

可得$\sum_{i=1}^n c_i\lambda_i=0$，所以：

$$\sum_{i=1}^n c_i\beta_i=\sum_{i=1}^n c_i(\alpha_i+ \delta^* \lambda_i)=\sum_{i=1}^n c_i\alpha_i$$

所以$\boldsymbol{\beta}$也是最优解。所以按照定理 1 中的流程，最终推得的基本可行解也是最优解，定理 2 得证。

---

综上，要找到原问题的一个最优解，在标准形中的基本可行解中寻找即可。$\boldsymbol{A}$至多有$C_{n}^{m}$个基，故至多有$C_{n}^{m}$个基本可行解，这就是我们的搜索空间。

3、单纯形法

基本步骤如下：

1. 选取一个初始可行基，确定初始基本可行解
2. 检查当前的基本可行解。若是最优解或发现无最优解，则结束；否则作基变换，用一个非基变量替换一个基变量，得到新的基和对应的基本可行解，且使目标函数值至少不增。

3.1、确定初始基本可行解

考虑最简单的情况，设约束条件为：

$$\sum_{j=1}^n a_{ij}x_j \leqslant 0, i=1, 2, \dots, m$$

其中$b_i\geqslant 0$。考虑引入$m$个松弛变量$x_{n+i}\geqslant 0$，约束变为：

$$\sum_{j=1}^n a_{ij}x_j +x_{n+i}=0, i=1, 2, \dots, m$$

选取$\{x_{n+i}\}$作为基向量，易得其基本可行解为$(0, 0, \dots, 0, b_1, b_2, \dots, b_m)^T$

3.2、最优性检验

考虑某个可行基$\boldsymbol{B}=(\boldsymbol{P}_{\pi (1)}, \boldsymbol{P}_{\pi (2)}, \cdots, \boldsymbol{P}_{\pi (m)})$（这里的$\pi(\cdot)$是一种映射，表示$\boldsymbol{B}$的第$i$个列向量对应着$\boldsymbol{A}$的第$\pi(i)$个列向量）。记$\boldsymbol{A}$中非基变量的列构成的矩阵为$\boldsymbol{N}$，有：

$$\boldsymbol{B}^{-1}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{B}^{-1}(\boldsymbol{B}\boldsymbol{x}_B+\boldsymbol{N}\boldsymbol{x}_N)=\boldsymbol{x}_B+\boldsymbol{B}^{-1}\boldsymbol{N}\boldsymbol{x}_N=\boldsymbol{B}^{-1}\boldsymbol{b}$$

可解得$\boldsymbol{x}_B=\boldsymbol{B}^{-1}\boldsymbol{b}-\boldsymbol{B}^{-1}\boldsymbol{N}\boldsymbol{x}_N$

代入目标函数：

$$z=\boldsymbol{c}^T\boldsymbol{x}=\boldsymbol{c}_B^T\boldsymbol{x}_B+\boldsymbol{c}_N^T\boldsymbol{x}_N=\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{b}+(\boldsymbol{c}_N^T-\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{N})\boldsymbol{x}_N$$

所以，对于基$\boldsymbol{B}$，其基本可行解$\boldsymbol{x}$由$\boldsymbol{x}_B=\boldsymbol{B}^{-1}\boldsymbol{b}$以及$\boldsymbol{x}_N=\boldsymbol{0}$构成，对应的目标函数值为$z_0=\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{b}$

---

将$z_0$代入，继续运算，得到简化的目标函数：

$$\begin{align*} z&=z_0+(\boldsymbol{c}_N^T-\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{N})\boldsymbol{x}_N=z_0+(\boldsymbol{c}_B^T-\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{B})\boldsymbol{x}_B+(\boldsymbol{c}_N^T-\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{N})\boldsymbol{x}_N \\ &=z_0+(\boldsymbol{c}^T-\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{A})\boldsymbol{x}=z_0+\boldsymbol{\lambda}^T\boldsymbol{x} \end{align*}$$

其中$\boldsymbol{\lambda}^T=\boldsymbol{c}^T-\boldsymbol{c}_B^T\boldsymbol{B}^{-1}\boldsymbol{A}$。

称$\boldsymbol{\lambda}$的分量$\lambda_1, \lambda_2, \dots, \lambda_n$为检验数，对应基变量的检验数必为 0。

---

记$\boldsymbol{B}^{-1}\boldsymbol{A}=\boldsymbol{\alpha}$，$\boldsymbol{\beta}= \boldsymbol{B}^{-1}\boldsymbol{b}$，$\boldsymbol{P}_j'=\boldsymbol{B}^{-1}\boldsymbol{P}_j=(\alpha_{1j}, \alpha_{2j}, \dots, \alpha_{mj})^T$

定理 3：对于可行基$\boldsymbol{B}$，给定其基本可行解$\boldsymbol{x}^{(0)}$，若$\lambda_i\geqslant 0, \forall i$，则$\boldsymbol{x}^{(0)}$是最优解；若存在$\lambda_k<0$且所有$\alpha_{ik}\leqslant 0$，则原问题无最优解。

证明：如果$\lambda_i \geqslant 0, \forall i$，则对任意可行解$\boldsymbol{x}$，必有$\boldsymbol{\lambda}^T\boldsymbol{x}\geqslant 0$，所以$z\geqslant z_0$，$\boldsymbol{x}^{(0)}$是最优解。

如果存在$\lambda_k<0$，由$\boldsymbol{\lambda}$的定义，$\lambda_k$一定对应某个非基变量。取$x_k=M>0$，其他非基变量取 0，可求得$x_{Bi}=\beta_i-\alpha_{ik}M\geqslant 0$，所以这也是一个可行解。其对应的目标函数值为$z=z_0+\lambda_k M+C$，其中$C$是基变量对应的分量，有$C\geqslant 0$。当$M\to +\infty$时，$z\to -\infty$，所以原问题无最优解。

---

还有一种可能的情况是，存在$\lambda_k<0$，但是$\alpha_{ik}$不全为非正数。这种情况，就要用到下面介绍的基变换，来进一步进行下去。

3.3、基变换

设$\lambda_k<0$且存在$\alpha_{lk}>0$，其对应的$x_k$一定是非基变量。进行基变换：用非基变量$x_k$替换基变量$x_{\pi (l)}$，对应得到新的基$\boldsymbol{B}'=\{\boldsymbol{P}_{\pi (1)}, \dots, \boldsymbol{P}_{\pi (l-1)}, \boldsymbol{P}_k, \boldsymbol{P}_{\pi (l+1)}, \dots, \boldsymbol{P}_{\pi (m)}\}$。称$\boldsymbol{x}_k$为换入变量，$\boldsymbol{x}_{\pi (l)}$为换出变量。

首先要证明$\boldsymbol{B}'$确实是一个基。只需证明$\boldsymbol{P}_{\pi (l)}$可以被$\boldsymbol{B}'$表示即可（因为$\boldsymbol{B}$是一组基，将这组基下的线性表示中的$\boldsymbol{P}_{\pi (l)}$换为$\boldsymbol{B}'$下的表示，就得到了纯$\boldsymbol{B}'$下的线性表示）。

由于$(\boldsymbol{P}_{\pi (1)}', \boldsymbol{P}_{\pi (2)}', \dots, \boldsymbol{P}_{\pi (m)}')=\boldsymbol{B}^{-1}\boldsymbol{B}=\boldsymbol{I}$，所以有$\boldsymbol{P}_k'=\sum_{i=1}^m \alpha_{ik}\boldsymbol{P}_{\pi (i)}'$。在两边同左乘$\boldsymbol{B}$，移项化简，最终可得：

$$\boldsymbol{P}_{\pi (l)}=\frac{1}{\alpha_{lk}}\boldsymbol{P}_k-\sum_{i\neq l}\frac{\alpha_{ik}}{\alpha_{lk}}\boldsymbol{P}_{\pi (i)}$$

因此，$\boldsymbol{B}'$确实是一个基。

---

由$(\boldsymbol{P}_{\pi (1)}', \boldsymbol{P}_{\pi (2)}', \dots, \boldsymbol{P}_{\pi (m)}')=\boldsymbol{B}^{-1}\boldsymbol{B}=\boldsymbol{I}$，将单位阵的第$i$列换成$\boldsymbol{P}_k'$得到$\boldsymbol{H}$，再左乘$\boldsymbol{B}$，实际上就得到了$\boldsymbol{B}'$对应的矩阵。也即有$\boldsymbol{B}'=\boldsymbol{B}\boldsymbol{H}$。于是有：

$$\boldsymbol{B}'^{-1}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{B}'^{-1}b\Leftrightarrow \boldsymbol{H}^{-1}\boldsymbol{B}^{-1}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{H}^{-1}\boldsymbol{B}^{-1}b=\boldsymbol{H}^{-1}\boldsymbol{\beta}$$

所以用$\boldsymbol{B}'$代替$\boldsymbol{B}$，等价于在原来的基础上左乘$\boldsymbol{H}^{-1}$。$\boldsymbol{H}^{-1}$具体如下：

$$\boldsymbol{H}^{-1}=\begin{bmatrix} 1 & \ & \ & -\alpha_{1k}/\alpha_{lk} & \ & \ & \ \\ \ & \ddots & \ &\vdots & \ & \ \\ \ & \ & 1 & -\alpha_{l-1,k}/\alpha_{lk} & \ & \ \\ \ & \ & \ & 1/\alpha_{lk} & \ & \ \\ \ & \ & \ & -\alpha_{l+1,k}/\alpha_{lk} & 1 & \ \\ \ & \ & \ & \vdots & \ & \ddots \\ \ & \ & \ & -\alpha_{mk}/\alpha_{lk} & \ & \ & 1 \end{bmatrix}$$

---

记$\boldsymbol{H}^{-1}\boldsymbol{B}^{-1}\boldsymbol{A}=\begin{bmatrix} \alpha'_{ij} \end{bmatrix}_{m\times n}$，$\boldsymbol{\beta}'= \boldsymbol{H}^{-1}\boldsymbol{B}^{-1}\boldsymbol{b}$

于是可以写出$\alpha'_{ij}$和$\beta_i'$的表达式：

$$\alpha'_{ij}=\begin{cases} \frac{\alpha_{lj}}{\alpha_{lk}} , & i=l \\ \alpha_{ij}-\frac{\alpha_{ik}\alpha_{lj}}{\alpha_{lk}} , & i\neq l \end{cases}$$

$$\beta_i'=\begin{cases} \frac{\beta_l}{\alpha_{lk}} , & i=l \\ \beta_i-\frac{\alpha_{ik}\beta_l}{\alpha_{lk}} , & i\neq l \end{cases}$$

直观理解，就是把变形后的约束方程$\boldsymbol{x}_B+\boldsymbol{B}^{-1}\boldsymbol{N}\boldsymbol{x}_N=\boldsymbol{B}^{-1}\boldsymbol{b}$中第$l$个方程中$x_l$的系数变为 1，然后用这个方程消去其他方程中的$x_l$。

要保证$\boldsymbol{B}'$是可行的，需要保证$\beta_i'\geqslant 0, \forall i$。由$\beta_i\geqslant 0, \forall i$以及$\alpha_{lk}>0$，所以$\alpha_{ik}\leqslant 0$时，有$\beta_i'\geqslant 0$成立。而$\alpha_{lk}>0$，要有:

$$\frac{\beta_l}{\alpha_{lk}}\leqslant \frac{\beta_i}{\alpha_{ik}}$$

因此，只需取$l=\arg\min_{i, \alpha_{ik}>0}\{ \beta_i/\alpha_{ik}\}$

---

相应的，对化简的目标函数也做类似的变换，得到基于$\boldsymbol{B}'$的简化目标函数，其中：

$$\begin{align*} \lambda_j'&=\lambda_j-\frac{\lambda_k\alpha_{lj}}{\alpha_{lk}}\\ z_0'&=z_0+\frac{\lambda_k\beta_l}{\alpha_{lk}} \end{align*}$$

直观上理解，用之前提到的化简后的第$l$个方程，消去$z=z_0+\boldsymbol{\lambda}^T\boldsymbol{x}$中的$x_k$。

3.4、单纯形法的完整叙述

1. 设初始可行基$\boldsymbol{B}=(\boldsymbol{P}_{\pi (1)}, \boldsymbol{P}_{\pi (2)}, \cdots, \boldsymbol{P}_{\pi (m)})$，$\boldsymbol{\alpha}= \boldsymbol{B}^{-1}\boldsymbol{A}$，$\boldsymbol{\beta}= \boldsymbol{B}^{-1}\boldsymbol{b}$，$\boldsymbol{\lambda}^T=\boldsymbol{c}^T-\boldsymbol{c}_B^T\boldsymbol{\alpha}$，$z_0=\boldsymbol{c}_B^T\boldsymbol{\beta}$
2. 若$\lambda_j\geqslant 0, 1\leqslant j\leqslant n$，则$\boldsymbol{x}_B=\boldsymbol{\beta}, \boldsymbol{x}_N=\boldsymbol{0}$组合出的$\boldsymbol{x}$是最优解，算法结束
3. 否则，任取一个$\lambda_k<0$。若所有$\alpha_{ik}\leqslant 0$，则原问题无最优解，算法结束
4. 否则存在$l$使得$\alpha_{lk}>0$，其中$l=\arg\min_{i, \alpha_{ik}>0}\{ \beta_i/\alpha_{ik}\}$
5. 以$x_k$为换入变量，$x_{\pi (l)}$为换出变量，进行基变换。回到步骤 2

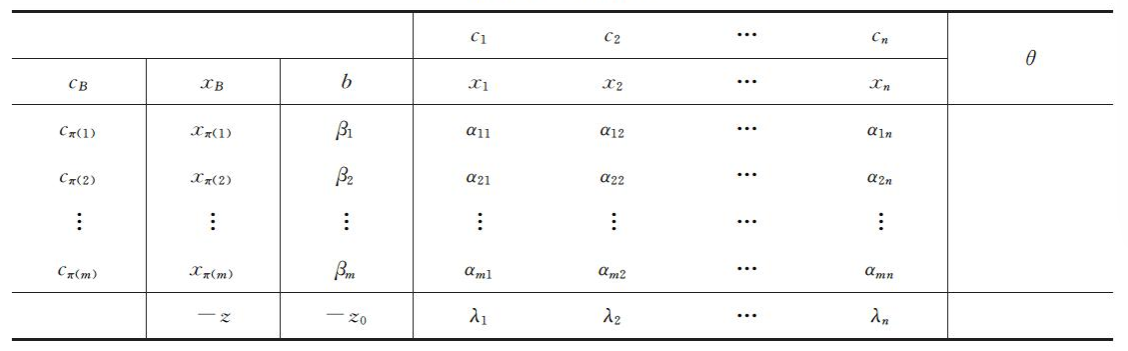
3.5、单纯形表

单纯形表如下图所示：

首先，来解释一下单纯形表的结构：

• 最中心的大矩形存放矩阵$\boldsymbol{\alpha}$
• $\boldsymbol{x}_B$列存放基变量，$\boldsymbol{c}_B$存放的是基变量对应的目标函数系数，$\boldsymbol{b}$列存放基变量的值
• 最后一行存放检验数$\boldsymbol{\lambda}$
• 将简化的目标函数改写为$-z+\sum_{j=1}^n \lambda_j \boldsymbol{x}_j=-z_0$，与$\sum_{j=1}^n \alpha_{ij}x_j=\beta_i$的形式统一起来。每一行就代表了其中一个等式。

由于选择的初始基$\boldsymbol{B}$是单位阵，所以一开始$\boldsymbol{\alpha}=\boldsymbol{A}$，$\boldsymbol{c}_B=\boldsymbol{0}$，$\boldsymbol{\lambda}=\boldsymbol{c}$

---

接下来讲述怎么利用单纯形表进行计算。

1. 初始化。按照上面的叙述，初始化单纯形表

2. 检查$\lambda_j$，如果全是非负，则已经得到最优解（由当前$\boldsymbol{c}_B$列和$\boldsymbol{b}$列每行逐对相乘再求和得到，也就是$z_0$值）。如果存在$\lambda_k<0$（有多个时，选$|\lambda_k|$最大的那个），检查$\boldsymbol{\alpha}$的第$k$列，如果该列全为非正数，则无最优解。

3. 否则，对每一个$\alpha_{ik}>0$，计算$\theta_i=\beta_i/\alpha_{ik}$，填到$\boldsymbol{\theta}$列中。假设$\theta_l$最小，将$\alpha_{lk}$圈起来，取$x_k$为换入变量，$x_{\pi (l)}$为换出变量，进行基变换。

4. 在单纯形表上做基变换的操作：

   • 更新$\boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\lambda}$。做一些行变换，在 3.3 基变换章节已经叙述过了。
   • 将$\boldsymbol{x}_B$列的$\boldsymbol{x}_{\pi (l)}$换成$\boldsymbol{x}_k$。将$\boldsymbol{c}_B$的$\boldsymbol{c}_{\pi (l)}$换成$\boldsymbol{c}_k$。

5. 这样，就得到了一张新的单纯形表，回到步骤 2

4、人工变量和两阶段法

4.1、人工变量

在 3.1 中，只讨论了对最简单的情况如何确定初始基本可行解。约束条件还有其他两种情况：

• $\sum_{j=1}^n a_{ij}x_j \geqslant b_i$
• $\sum_{j=1}^n a_{ij}x_j = b_i$

对于情况 1，引入剩余变量可以转化为情况 2。对于情况 2，引入人工变量$y_i\geqslant 0$，将约束变为：

$$\sum_{j=1}^n a_{ij}x_j +y_i = b_i$$

一开始取所有的松弛变量和人工变量得到初始可行基，以及相应初始基本可行解。

4.2、两阶段法

引入人工变量后求解，最终得到的解中，只有所有的人工变量值均为 0 时，才能直接舍弃掉人工变量，得到原问题的解。否则，是不满足约束条件的。

设原问题为：

$$\begin{align*} \min z=\sum_{j=1}^n c_jx_j\\ \text{s.t.} \sum_{j=1}^n a_{ij}x_j = b_i, & 1\leqslant i\leqslant m\\ x_j\geqslant 0,& 1\leqslant j\leqslant n \end{align*}$$

引入人工变量$x_{n+i}, 1\leqslant i\leqslant m$，引入一个辅助问题：

$$\begin{align*} \min w=\sum_{i=1}^m x_{n+i}\\ \text{s.t.} \sum_{j=1}^n a_{ij}x_j +x_{n+i} = b_i, & 1\leqslant i\leqslant m\\ x_j\geqslant 0,& 1\leqslant j\leqslant n+m \end{align*}$$

由于$w\geqslant 0$，所以辅助问题必有最优解。设其最优解为$(x_1^*, x_2^*, \dots, x_{n+m}^*)$，最优值为$w^*$，有以下三种情况：

• $w^*>0$，则原问题无可行解
• $w^*=0$且最优解中所有人工变量都是非基变量，也即$x_{n+i}^*=0, 1\leqslant i\leqslant m$，则$(x_1^*, x_2^*, \dots, x_n^*)$是原问题的基本可行解
• $w^*=0$但最优解中有人工变量是基变量。仍有$x_{n+i}^*=0, 1\leqslant i\leqslant m$，不妨先假设只有$x_{n+k}$是基变量。考虑解该辅助问题时最终的单纯形表中，$x_{n+k}$对应的行，假设在第$r$行。由$\boldsymbol{\alpha x}=\boldsymbol{\beta}$有：

  $$\sum_{j=1}^{m+n} \alpha_{rj}x_j=\beta_r \Leftrightarrow \sum_{j=1}^{n} \alpha_{rj}x_j+1\cdot x_{n+k}+ \sum_{1\leqslant j\leqslant m, j\neq k} \alpha_{r, {n+j}}x_{n+j}=0$$

  说明原问题中$m$个约束等式并不是线性无关的（用单纯形表进行计算，本质上是不停的对$\begin{bmatrix} \boldsymbol{\alpha} & \boldsymbol{\beta} \end{bmatrix}$进行行变换，这里组合出了非平凡的零解）。
  • 如果$\alpha_{rj}, 1\leqslant j\leqslant n$全为 0，说明引入$x_{n+k}$的那个约束是冗余的，可以直接删掉
  • 如果存在$\alpha_{rl} \neq 0$，以$x_{l}$为换入变量，$x*{n+k}$为换出变量，进行基变换。由于$\beta*{r}=0$，所以这个基变换不会改变$\boldsymbol{\beta}$列，也不会改变$w$的值，但是使基变量中的人工变量变少了。

所以如果$w^*=0$，最终总能变成情况 2，保证基变量中没有人工变量。

5、单纯形法的有限终止

如果基本可行解中基变量的值都大于 0, 则称这个基本可行解是非退化的, 否则称作退化的。

如果线性规划的所有基本可行解都是非退化的, 则称这个线性规划是非退化的。如果线性规划有可行解并且是非退化的, 则每一次基变换都会使目标函数值严格下降，从而在计算过程中，可行基不会从夫出现，因此单纯形法一定会在有限步内终止。

Bland 规则指出：

• 当有多个$\lambda_j<0$时，去对应的非基变量中下标最小的那个作为换入变量
• 当有多个$\theta_i=\beta_i/\alpha_{ik}$同时取到最小值时，取对应的基变量中下标最小的那个作为换出变量

按照 Bland 规则选取换入换出变量，可以保证单纯形法的有限终止。

6、对偶性

设线性规划：

$$\begin{align*} \max \boldsymbol{c}^T\boldsymbol{x}\\ \text{s.t.} \boldsymbol{A}\boldsymbol{x}\leqslant \boldsymbol{b}\\ \boldsymbol{x}\geqslant \boldsymbol{0} \end{align*}$$

其对偶线性规划（也简称对偶/对偶规划）为：

$$\begin{align*} \min \boldsymbol{b}^T\boldsymbol{y}\\ \text{s.t.} \boldsymbol{A}^T\boldsymbol{y}\geqslant \boldsymbol{c}\\ \boldsymbol{y}\geqslant \boldsymbol{0} \end{align*}$$

第七章 网络流算法

1、有向图

图、节点、边的概念不在此赘述。

有向图可记作$G=(V, E)$，其中$V$是节点集合，$E$是边集合。每条边$e\in E$可以表示为一个有序对$(i, j)$，其中$i, j\in V$，表示从节点$i$到节点$j$的一条边。

从一个节点出发，到达另一个节点，所经过的边的序列称为一条路径。路径上边的个数称为路径的长度。

如果一个有向图从其中任何一个节点出发可以到达其他任何一个节点，则称这个有向图是强连通的。

如果从有向图的一个节点出发到返回这个节点的路径的长度都是$k$的倍数（$k>1, k\in \mathcal{N}$），则称这个节点是周期性节点。如果一个有向图不含周期性节点，则称这个有向图是非周期性图（Aperiodic Graph），否则为周期性图。

2、随机游走模型

给定一个含有$n$个节点的有向图，在有向图上定义随机游走模型，也即一阶马尔科夫链。其中节点表示状态，有向边表示状态之间的转移。假设一个节点通过有向边到达其他节点的概率是相同的。

具体来说，转移矩阵$\boldsymbol{M}\in \mathbb{R}^{n\times n}$，其中$\boldsymbol{M}_{ij}$表示从节点$j$到节点$i$的概率。假设节点$j$有$k$条出边，对于$j$连出的节点$i$，有$\boldsymbol{M}_{ij}=1/k$；对于其他节点，$\boldsymbol{M}_{ij}=0$。

显然，转移矩阵满足以下性质：

• $m_{ij}\geqslant 0$
• $\sum_{i=1}^n m_{ij}=1, \forall j$

转移矩阵就是一个随机矩阵。

---

随机游走者每经过一个单位时间转移一个状态，假设当前时刻在第$j$个节点（状态为$j$），下一个时刻转移到第$i$个节点的概率为$\boldsymbol{M}_{ij}$。显然，这一概率只依赖于当前状态，与过去的状态无关，具有马尔科夫性质，构成一个一阶马尔科夫链。

随机游走者在某个时刻$t$访问各个节点的概率，可以用一个$n$维列向量$R_t$表示，这也就是马尔科夫链在$t$时刻的状态分布。则有：

$$R_{t+1}=\boldsymbol{M}^T R_t$$

3、PageRank 问题

将网页看作节点，网页之间的跳转看作边，构成一个有向图。浏览者随机浏览网页，构成一个随机游走模型。

PageRank 是一个函数，输入是网页，输出是一个实数值，表示这个网页的重要性。得到 PageRank 值的一种方法是：假定浏览者随机游走的情况下，考虑其某个时刻停留在某个页面的概率，这个概率值就作为这个页面的 PageRank 值。所以 PageRank 就是该随机游走模型的平稳分布，每个页面的 PageRank 值就是平稳概率。

3.1、基本定义

给定一个包含$n$个节点$v_1, v_2, \dots, v_n$的强连通的，非周期性的有向图。在有向图上定义随机游走模型，即一阶马尔科夫链，其转移矩阵为$\boldsymbol{M}$。这个马尔科夫链具有平稳分布$\boldsymbol{R}$，称其为这个有向图的 PageRank。$\boldsymbol{R}$的各个分量称为各个节点的 PageRank 值，记为$PR(v_i)$。

---

考虑在时刻$0, 1, 2, \dots, t, \dots$，访问各个节点的概率分布为$\boldsymbol{R}_0, \boldsymbol{M}\boldsymbol{R}_0, \boldsymbol{M}^2\boldsymbol{R}_0, \dots, \boldsymbol{M}^t\boldsymbol{R}_0, \dots$

由于不可约且非周期的有限状态马尔科夫链，由唯一平稳分布存在，并且当时间趋于无穷时的状态分布收敛于唯一的平稳分布。PageRank 问题的基本定义满足上述条件，所以极限：

$$\lim_{t\to +\infty} \boldsymbol{M}^t\boldsymbol{R}_0=\boldsymbol{R}$$

存在。极限值$\boldsymbol{R}$就表示平稳分布，满足$\boldsymbol{M}\boldsymbol{R}=\boldsymbol{R}$。

---

记$M(v_i)$为存在到$v_i$的出边的节点的集合，$L(v_j)$为节点$v_j$的出度。

PageRank 值满足以下性质：

• $PR(v_i)\geqslant 0$
• $\sum_{i=1}^n PR(v_i)=1$
• $PR(v_i)=\sum_{v_j\in M(v_i)}\frac{PR(v_j)}{L(v_j)}$

---

PageRank 的定义是明确的，可以通过迭代的方式求出$\boldsymbol{R}$。

3.2、一般定义

有时候有向图并不满足强连通和非周期性的条件，则此时不一定能够得到有意义的$\boldsymbol{R}$。

这就引出了 PageRank 的一般定义，其基本思想是在基本定义的基础上加入平滑项。考虑另一个完全随机游走模型，其转移矩阵的元素全部为$1/n$。两个转移矩阵的线性组合构成一个新的转移矩阵，可以证明，其对应的马尔科夫链存在平稳分布$\boldsymbol{R}$，满足

$$\boldsymbol{R}=d \boldsymbol{M}\boldsymbol{R}+\frac{1-d}{n}\boldsymbol{1}$$

其中$\boldsymbol{1}$为全 1 向量，$d\in [0, 1]$是阻尼因子（Damping Factor），取值由经验决定。当$d$接近 1 时，表示随机游走主要依据原始转移矩阵进行；当$d$接近 0 时，表示随机游走主要依据完全随机游走模型进行。

---

一般定义下的 PageRank 值满足以下性质：

$$PR(v_i)=d\left(\sum_{v_j\in M(v_i)}\frac{PR(v_j)}{L(v_j)}\right)+\frac{1-d}{n}$$

等式右边第二项极为平滑项，它保证了\PR(v_i)>0，且仍有$\sum_{i=1}^n PR(v_i)=1$。

3.3、PageRank 的计算

3.3.1、迭代法

有定义，直接按照以下迭代公式进行迭代即可，直到收敛或达到某种精度：

$$\boldsymbol{R}_{t+1}=d\boldsymbol{M}\boldsymbol{R}_t+\frac{1-d}{n}\boldsymbol{1}$$

3.3.2、幂法

考虑矩阵$\boldsymbol{A}\in\mathbb{R}^{n\times n}$。假设其有$n$个特征值$|\lambda_1|>|\lambda_2|\geqslant \dots \geqslant |\lambda_n|$，对应的特征向量为$\boldsymbol{u}_1, \boldsymbol{u}_2, \dots, \boldsymbol{u}_n$。称$\lambda_1$为$\boldsymbol{A}$的主特征值，$\boldsymbol{u}_1$为对应的主特征向量。幂法用于近似求解主特征向量。

$n$个特征向量构成$n$维空间的一组基。任取一个初始向量$\boldsymbol{x_0}$，用这组基表示为$x_0=\sum_{i=1}^n a \boldsymbol{u}_i$。假设$\lambda_1$是特征方程的单根，则有：

$$\boldsymbol{x_k}=\boldsymbol{A}^k x_0=\sum_{i=1}^n a \lambda_i^k \boldsymbol{u}_i=a_1 \lambda_1^k \left[\boldsymbol{u}_1+\sum_{i=2}^n \left(\frac{\lambda_i}{\lambda_1}\right)^k a_i \boldsymbol{u}_i\right]$$

所以有：

$$\lim_{k\to +\infty}\boldsymbol{x_k}= a_1 \lambda_1^k \boldsymbol{u}_1$$

也即$k$充分大时，$\boldsymbol{x_k}$与$\boldsymbol{u}_1$仅相差一个系数。

---

一般 PageRank 中，转移矩阵可写为：

$$\boldsymbol{R}=d \boldsymbol{M}\boldsymbol{R}+\frac{1-d}{n}\boldsymbol{1}=\left(d \boldsymbol{M}+\frac{1-d}{n}\boldsymbol{E}\right)\boldsymbol{R}=\boldsymbol{A}\boldsymbol{R}$$

其中$\boldsymbol{E}$为全 1 矩阵（由于$\sum_{i=1}^n R_i=1$，所以有$\boldsymbol{E}\boldsymbol{R}=\boldsymbol{1}$）

由 Perron-Frobenius 定理，$\boldsymbol{R}$是$\boldsymbol{A}$的主特征向量。所以，可以用幂法求出 PageRank。

为了防止计算过程中出现绝对值过大或者过小的情况，过程中对$\boldsymbol{x}_k$要进行规范化处理：$\boldsymbol{x}_k\leftarrow\boldsymbol{x}_k/\|\boldsymbol{x}_k\|$。

3.3.3、直接法

根据定义，可以直接写出$\boldsymbol{R}$的表达式：

$$\boldsymbol{R}=\frac{1-d}{n}(\boldsymbol{I}-d\boldsymbol{M})^{-1}\boldsymbol{1}$$

求解一个逆矩阵即可。

4、最大流问题

4.1、定义

定义容量网络$N=(V, E, c, s, t)$，其中：

• $(V, E)$是有向连通图, 记$n=|V|, m=|E|$
• $c:E\to \mathbb{R}^+$是边的容量函数，表示边能够通过的最大流量
• $s, t\in V$是两个特殊的节点，分别是源点（发点）和汇点（收点），其余节点称为中间点。

---

流可以用一个函数$f: E\to \mathbb{R}^+$来表示，函数值表示边上的流量。若其满足下列条件（其中$f((i, j))$简记为$f(i, j)$，函数$c$同理）：

• 容量限制：$f(i, j)\leqslant c(i, j), \forall (i, j)\in E$，也即每条边上的流量不能超过其容量
• 平衡条件：$\sum_{(j, i) \in E} f(j, i)-\sum_{(i, j)\in E} f(i, j)=0, \forall i\in V-\{s, t\}$，也即中间点上流入量等于流出量

则称$f$是网络$N$上的一个可行流。

---

称源点$s$的净流出量为$f$的流量，记作$v(f)$:

$$v(f)=\sum_{(s, i)\in E} f(s, i)-\sum_{(i, s)\in E} f(i, s)$$

流量最大的流称为最大流。显然有：

$$v(f)=\sum_{(i, t)\in E} f(i, t)-\sum_{(t, i)\in E} f(t, i)$$

也即源点的净流出量等于汇点的净流入量。

---

最大流问题的线性规划形式可以写为：

$$\begin{align*} \max & v(f)\\ \text{s.t.} & f(i, j)\leqslant c(i, j), \forall (i, j)\in E\\ & \sum_{(j, i) \in E} f(j, i)-\sum_{(i, j)\in E} f(i, j)=0, \forall i\in V-\{s, t\}\\ & v(f)=\sum_{(s, i)\in E} f(s, i)-\sum_{(i, s)\in E} f(i, s) \\ & f(i, j)\geqslant 0, \forall (i, j)\in E\\ & v(f)\geqslant 0 \\ \end{align*}$$

能够求解线性规划的算法都能够求解最大流问题，但是最大流问题应用广泛，有很多专门的算法。

4.2、最小割集

设容量网络$N=(V, E, c, s, t)$，考虑将顶点集划分为两个集合，源点和汇点分别在两个集合中。也即$A\subset V$且$s\in A, t\in \overline{A}$，则称：

$$(A, \overline{A})=\{(i, j)\in E|i\in A, j\in \overline{A}\}$$

为$N$的一个割集。

扩展容量函数$c$的定义，对整个割集求容量：

$$c(A, \overline{A})=\sum_{(i, j)\in (A, \overline{A})} c(i, j)$$

容量最小的割集就称为最小割集。

---

引理 1：若$f$是$N$上的一个可行流，$(A, \overline{A})$是一个割集，则有：

$$v(f)=\sum_{(i, j)\in (A, \overline{A})} f(i, j)-\sum_{(j, i)\in (A, \overline{A})} f(j, i)$$

也即整个网络上的流量，等于割集上的流量。

证明：从$v(f)$的定义出发，利用平衡条件，导出两者相等：

$$\begin{align*} v(f)&=\sum_{(s, i)\in E} f(s, i)-\sum_{(i, s)\in E} f(i, s)\\ &=\sum_{(s, i)\in E} f(s, i)-\sum_{(i, s)\in E} f(i, s)+\sum_{i\in A-\{s\}}\left(\sum_{(j, i)\in E} f(j, i)-\sum_{(i, j)\in E} f(i, j)\right)\\ &=\sum_{i\in A}\left(\sum_{(j, i)\in E} f(j, i)-\sum_{(i, j)\in E} f(i, j)\right)\\ &=\sum_{i\in A}\sum_{(i, j)\in E} f(i, j)-\sum_{i\in A}\sum_{(j, i)\in E} f(j, i)\\ &=\left(\sum_{i\in A, j\in A}\sum_{(i, j)\in E} f(i, j)+\sum_{i\in A, j\in \overline{A}}\sum_{(i, j)\in E} f(i, j)\right)-\left(\sum_{i\in A, j\in A})\sum_{(j, i)\in E} f(j, i)+\sum_{i\in A, j\in \overline{A}}\sum_{(j, i)\in E} f(j, i)\right)\\ &=\sum_{(i, j)\in (A, \overline{A})} f(i, j)-\sum_{(j, i)\in (A, \overline{A})} f(j, i) \end{align*}$$

---

引理 2：若$f$是$N$上的一个可行流，$(A, \overline{A})$是一个割集，则有：

$$v(f)\leqslant c(A, \overline{A})$$

证明：

$$\begin{align*} v(f)&=\sum_{(i, j)\in (A, \overline{A})} f(i, j)-\sum_{(j, i)\in (A, \overline{A})} f(j, i)\\ &\leqslant \sum_{(i, j)\in (A, \overline{A})} f(i, j)\\ & \leqslant \sum_{(i, j)\in (A, \overline{A})} c(i, j)=c(A, \overline{A}) \end{align*}$$

---

由引理 1、2，显然有引理 3：设$f$是$N$上的一个可行流，$(A, \overline{A})$是一个割集。若$v(f)=c(A, \overline{A})$，则$f$是最大流，$(A, \overline{A})$是最小割集。

这就是最大流最小割定理。

4.3、最小割集的一个应用

经营投资策略问题。假设开发产品$A_i$需要先购进$m_i$个工具$T_{i_1}, T_{i_2}, \dots, T_{i_{m_i}}$，工具$T_i$的价格为$Q_i$（每件工具只能用于一种产品的开发），产品$A_i$的收益为$P_i$。求选择哪些产品开发，使得利润最大。

---

考虑构建一个这样的容量网络：

如果产品$A_i$需要工具$T_j$，就拉一条从$T_j$到$A_i$的边，容量无限大的边。

以选择开发所有正净利润产品为例。将净利润为正的产品以及所需工具，放入源点集合$A$；净利润为负的产品，放入汇点集合$\overline{A}$。分析割集的容量，割集中的边包括：

• 从源点到正净利润产品所需的边，这些边的容量之和代表成本
• 从负净利润产品到汇点的边，这些边的容量之和代表负净利润产品的收益，我们不开发这些产品

用所有产品的利润之和减掉这个割集的容量，就是最终的收益。所以，用所有产品的利润之和减掉最小割集的容量，就能得到最大收益。

4.4、增广链

设$f$是$N$上的一个可行流，定义以下概念：

• 饱和边：流量等于容量的边
• 非饱和边：流量小于容量的边
• 零流边：流量为 0 的边
• 非零流边：流量不为 0 的边

---

$N$中从节点$i$到$j$的一条无重复边的路径（不考虑边的方向）称之为i-j 链。i-j 链的方向是从$i$到$j$，链中与链方向一致的边称为前向边，与链方向相反的边称为后向边。

i-j 增广链是前向边均为非饱和边，后向边均为非零流边的 i-j 链。

---

如果$N$上存在一条关于可行流$f$的 s-t 增广链，记$E_f, E_b$分别为增广链上的前向边和后向边，令：

$$\delta=\min\{\min_{e\in E_f} (c(e)-f(e)), \min_{e\in E_b} f(e)\}$$

可以构造一个新的流：

$$f'(e)=\begin{cases} f(e)+\delta, & e\in E_f\\ f(e)-\delta, & e\in E_b\\ f(e), & otherwise \end{cases}$$

易有，$f'$也是一个可行流，且$v(f')=v(f)+\delta$，比原可行流的流量增加了$\delta$。

---

定理：可行流$f$是最大流，当且仅当不存在关于$f$的 s-t 增广链。

证明：由上面的叙述以及反证法，易证得必要性。下面证明充分性。

假设不存在关于$f$的 s-t 增广链。考虑所有以$s$为起点的增广链的终点$j$的集合$A$，由假设有$t\notin A$。割集$(A, \overline{A})$一定满足：

• $f(i, j)=c(i, j), \forall (i, j)\in (A, \overline{A})$
• $f(i, j)=0, \forall (i, j)\in (\overline{A}, A)$

对于其中第一点，若不然，存在$(i, j)\in (A, \overline{A})$，使得$f(i, j)<c(i, j)$，则 s-i 增广链延伸得到 s-j 链也是增广链，而 $j\in \overline{A}$，矛盾。第二点，同理可证。

于是：

$$v(f)=\sum_{(i, j)\in (A, \overline{A})} f(i, j)-\sum_{(j, i)\in (A, \overline{A})} f(j, i)=\sum_{(i, j)\in (A, \overline{A})} c(i, j)=c(A, \overline{A})$$

由引理 3，可知$f$是最大流。

5、Ford-Fulkerson 算法

简称 FF 算法，是解决最大流问题的一个经典算法。其基本思想是不断寻找增广链，修改链上的流量，直到不存在增广链为止，从而得到最大流。

---

从$s$开始，逐个给顶点作标号，直到$t$得到标号为止。某个顶点$j$得到标号，表示已经找到从$s$到$j$的增广链，标号为$(l_j, \delta_j)$。其中：

• $l_j=+i$，表示增广链上$j$的前一个顶点是$i$，且$(i, j)$是前向边；$l_j=-i$，表示增广链上$j$的前一个顶点是$i$，且$(j, i)$是后向边
• $\delta_j$是目前增广链上的$\delta$

---

将顶点分为三类：已标号已检查的、已标号未检查的$T$、未标号的$R$。FF 算法的完整流程叙述如下：

1. 一开始，所有的点都是未标号的$R=V$，边上的流量全为 0（零流）。
2. 给$s$标号$(\Delta, +\infin)$，$T=\{s\}, R=V-\{s\}$
3. 从$T$中选取一个顶点$i$，循环遍历$R$中所有与$i$邻接的所有顶点$j$：
   • 如果$f(i, j)<c(i, j)$，则给$j$标号$(+i, \delta_j)$。其中$\delta_j=\min\{\delta_i, c(i, j)-f(i, j)\}$
   • 如果且$f(j, i)>0$，则给$j$标号$(-i, \delta_j)$。其中$\delta_j=\min\{\delta_i, f(j, i)\}$
     $i$移出$T$，$j$从$R$移入$T$。
4. 第 3 步中，若某轮循环中$j=t$，说明找到了一条 s-t 增广链，该轮循环结束后，转入步骤 5；否则，重复步骤 2，直到$T$为空。如果直到$T$为空，都没有找到$s-t$增广链，说明已经是最大流，结束算法。
5. 从$t$开始，沿着标号链回溯，修改流量。具体而言：

   $$\begin{cases} f(i, j)\leftarrow f(i, j)+\delta_j, j\leftarrow i, & l_j=+i\\ f(j, i)\leftarrow f(j, i)-\delta_j, j\leftarrow i, & l_j=-i \end{cases}$$

   直到回溯到$s$，返回步骤 2。

---

假设所有的容量都是正整数，记$C=\sum_{(i, j)\in E} c(i, j)$。由于每次修改，流量至少增加 1，至多需要修改$C$次。修改一次，至多需要$O(m)$的时间，所以 FF 算法的时间复杂度为$O(mC)$。

计算机中，数的表示有一定的精度，所以算法总能在有限步内终止。理论上，容量为无理数时，$\delta$会越来越小，趋向于 0，算法不能在有限步终止。

6、Dinic 算法

FF 算法中，并没有明确给出标号过程的细节，找到的增广链以及找到不同增广链的顺序都是不固定的。而且 FF 算法每次只找一条增广链，就要重新标号，实际上也是一种浪费。

Dinic 算法对此进行了改进：

• 每次求最短的 s-t 增广链
• 充分利用一次标号的信息，每次找出尽可能多的增广链

6.1、辅助网络

定义一个关于容量网络$N$和其上一个可行流$f$的辅助网络 $N_f=(V, E_f, ac, s, t)$，其中：

• $E_f^+=\{(i, j)|(i, j)\in E, f(i, j)<c(i, j)\}$，$E_f^-=\{(j, i)|(i, j)\in E, f(i, j)>0\}$
• $E_f=E_f^+\cup E_f^-$

$ac$是辅助容量函数，定义如下：

$$ac(i, j)=\begin{cases} c(i, j)-f(i, j), & (i, j)\in E_f^+\\ f(j, i), & (i, j)\in E_f^-\\ \end{cases}$$

显然$N_f$也是一个容量网络。

---

引理 4：设$N$的最大流量是$v^*$，$f$是$N$上的一个可行流，则$N_f$的最大流量是$v^*-v(f)$。

证明：由于$N$和$N_f$的点击相同。$N$中的一个割集$(A, \overline{A})$，$N_f$中也可以基于这两个集合定义出相应割集$(A, \overline{A})_f$，其容量：

$$\begin{align*} ac(A, \overline{A})_f&=\sum_{(i, j)\in E_f^+}[c(i, j)-f(i, j)]+\sum_{(i, j)\in E_f^-}f(j, i)\\ &=\sum_{(i, j)\in (A, \overline{A})}[c(i, j)-f(i, j)]+\sum_{(i, j)\in (\overline{A}, A)}f(j, i)\\ &=\sum_{(i, j)\in (A, \overline{A})}c(i, j)-\left[\sum_{(i, j)\in (A, \overline{A})}f(i, j)-\sum_{(i, j)\in (\overline{A}, A)}f(j, i)\right]\\ &=c(A, \overline{A})-v(f) \end{align*}$$

由最大流最小割定理即得证。

---

设$f$是$N$上的一个可行流，$g$是$N_f$上的一个可行流，补充定义$g(i, j)=0, \forall (i, j)\notin E_f$。定义$E$上的$f'=f+g$如下：

$$f'(i, j)=f(i, j)+g(i, j)-g(j, i), \forall (i, j)\in E$$

---

引理 5：$f'$是$N$上的一个可行流，且$v(f')=v(f)+v(g)$。

证明：首先证明$f'$是一个可行流，要满足容量限制和平衡条件。

对于容量限制条件，由于$0\leqslant g(i, j)\leqslant c(i, j)-f(i, j), 0\leqslant g(j, i)\leqslant f(i, j)$，所以：

$$0\leqslant f'(i, j)=f(i, j)+g(i, j)-g(j, i)\leqslant c(i, j)$$

得证。

对于平衡条件，只需证对于所有中间点$i$有$\sum_{(j, i)\in E} f'(j, i)-\sum_{(i, j)\in E} f'(i, j)=0$。$\forall i\in V-\{s, t\}$，有：

$$\begin{align*} \sum_{(j, i)\in E} f'(j, i)&=\sum_{(j, i)\in E} f(j, i)+\sum_{(j, i)\in E, (j, i)\in E_f}g(j, i)-\sum_{(j, i)\in E, (i, j)\in E_f}g(i, j)\\ \sum_{(i, j)\in E} f'(i, j)&=\sum_{(i, j)\in E} f(i, j)+\sum_{(i, j)\in E, (i, j)\in E_f}g(i, j)-\sum_{(i, j)\in E, (j, i)\in E_f}g(j, i) \end{align*}$$

所以：

$$\begin{align*} \sum_{(j, i)\in E} f'(j, i)-\sum_{(i, j)\in E} f'(i, j)&=\left[\sum_{(j, i)\in E} f(j, i)-\sum_{(i, j)\in E} f(i, j)\right]+\left[\sum_{(j, i)\in E_f}g(j, i)-\sum_{(i, j)\in E_f}g(i, j)\right]\\ &=0+0=0 \end{align*}$$

得证。

同理，可证得$v(f')=v(f)+v(g)$。

6.2、分层辅助网络

在$N_f$中，记顶点$i$在以$s$为起点的广度优先生成树中的层数为$d(i)$（$s$在第 0 层）。定义$N_f$的分层辅助网络$AN_{f}=(V_f, AE_f, ac, s, t)$，其中：

• $V_{f}^{(k)}=\{i\in V_f|d(i)=k\}, 0\leqslant k\leqslant d(t)$
• $V_f=\bigcup_{k=0}^{d(t)} V_f^{(k)}$

分层辅助网络的边集定义为：

$$AE_f=\bigcup_{k=0}^{d(t)-1}\{(i, j)\in E_f|i\in V_f^{(k)}, j\in V_f^{(k+1)}\}$$

以下是一个带可行流的原始流量网络以及显影的辅助网络和分层辅助网络的示例，可以帮助理解三个网络的定义以及之间的关系：

可以浅显地理解为，多层辅助网络是按照广度优先搜索顺序进行搜索时，看到的网络。

6.3、Dinic 最大流算法

定义分层辅助网络中，每一个顶点$i$的流通量$th(i)$:

$$th(i)=\min\{\sum_{(j, i)\in AE_f} ac(j, i), \sum_{(i, j)\in AE_f} ac(i, j)\}$$

则 Dinic 最大流算法的完整叙述如下：

1. 对于原始网络$N$以及零流$f$，构建$AN(f)$
2. 如果$AN(f)$不存在从$s$到$t$的路径，返回当前$f$，这就是$N$的最大流，结束算法；否则进入步骤 3
3. 初始化流$g$为零流。
4. 查看$AN_f$中，流通量为 0 的顶点。如果其中包含$s$或者$t$，直接令$f\leftarrow f+g$，返回步骤 2；否则，删去这些顶点以及与其相连的边。
5. 找到流通量最小的顶点$k$，从$k$开始，将$th(k)$个单位的流往两边推送分别到达$s$和$t$（由流通量的定义，如果流要分流给多条边，一定是每条边都恰好占满），同时更新$g$。然后删掉$k$以及与其相连的边。
6. 对于$AN_f$中的每一条边，如果$g(i, j)=ac(i, j)$，则删去这条边；否则$ac(i, j)\leftarrow ac(i, j)-g(i, j)$，回到步骤 4。

6.4、Dinic 算法的细节

6.5、简单容量网络上的 Dinic 算法

6.6、Dinic 算法的时间复杂度

Dinic 算法在$O(n^3)$步内终止。

简单容量网络上，Dinic 算法在$O(n^{1/2}m)$步内终止。

（待补充）

7、最大流的应用

7.1、不相交路径问题

Edge Disjoint Paths，不相交路径。有向图上，对于给定的两个顶点，如果这两个顶点之间的两条路径没有公共边，就称这两条路径是不相交的。对于给定的两个顶点，求可以同时存在的不相交路径的最大条数。

---

考虑将给定的两个顶点看作源点和汇点，所有边的容量都设为 1（保证只能有 1 个单位的流流过，也即只能走一次。在这样的容量网络上求最大流，最大流的流量即为答案。

---

对于由多个起点和多个终点的不相交路径问题。考虑额外引入一个超级源点和一个超级汇点，超级源点到每个起点连一条容量无限的边，每个终点到超级汇点也连一条容量无限的的边。在这样的容量网络上求最大流，就可以得出结果了。

7.2、顶点存在容量限制的最大流

假设顶点也有容量，表示最多有多少流量能够流入该节点。

假设顶点$v$有容量限制$c(v)$，考虑创建一个新顶点$v'$，从$v$到$v'$连一条容量为$c(v)$的边，然后将所有原来$v$的出边改为从$v'$出发。这样，就加个顶点容量转化为了边的容量，变成了普通的最大流问题。

（证明待补充）

7.3、独立路径问题

起点和终点相同的两条路径，如果其没有其他的公共顶点，就称这两条路径是独立的。对于给定的起点和终点，求可以同时存在的独立路径的最大条数。

---

给所有的中间点设置 1 的顶点容量限制。由 7.2 的方法，转化为普通最大流问题求解即可。

8、Floyd-Warshall 算法

也常简称为 Floyd 算法，这是一种在带负权边的图上求最短路径和检测负回路的算法

带权有向图$D=(V, E, w)$，其中$w: E\rightarrow R$是权函数，函数值代表边的权值。$D$中权为负数的回路称之为负回路。

$D$中任意两点之间要么有最短路径，要么不存在路径当且仅当$D$中不存在负权回路。

---

记$d^{(k)}(i, j)$为从$i$到$j$，只经过$\{1, 2, \dots, k\}$的顶点的最短路径长度。则有递推关系：

$$d^{(k)}(i, j)=\begin{cases} w(i, j), & k=0\\ \min\{d^{(k-1)}(i, j), d^{(k-1)}(i, k)+d^{(k-1)}(k, j)\}, & 1\leqslant k\leqslant n, 1\leqslant i, j\leqslant n, i\neq k, j\neq k \end{cases}$$

规定$w(i, i)=0$，且对$(i, j)\notin E$，$w(i, j)=+\infin$。

若$D$中存在负回路，假设负回路经过$i$，回路中除$i$外顶点的最大号码为$k$，则一定有$d^{(k)}(i, i)<0$。

---

Floyd-Warshall 算法的时间复杂度为$O(n^3)$。

9、最小费用流

9.1、定义

在容量网络$N=(V, E, c, s, t)$的基础上，添加费用函数$w: E\rightarrow R$，表示每条边的单位流量费用，得到容量-费用网络$N=(V, E, c, w, s, t)$。

设$f$是$N$上的一个可行流，称$w(f)=\sum_{(i, j)\in E} w(i, j)f(i, j)$为$f$的费用。所有流量为$v$的可行流中，费用最小的称为流量$v$的最小费用流。

---

容量-费用网络上也可以定义关于可行流$f$的辅助网络$N_f=(V, E_f, ac, aw, s, t)$。其中$E_f$和$ac$的定义与之前相同，辅助费用的定义如下：

$$aw(i, j)=\begin{cases} w(i, j), & (i, j)\in E_f^+\\ -w(j, i), & (i, j)\in E_f^- \end{cases}$$

也有类似的引理：设$f$是容量-费用网络$N$上的可行流，$g$是辅助网络$N_f$上的可行流，则$f'=f+g$也是$N$上的一个可行流，且$w(f')=w(f)+aw(g)$。

9.2、圈流

设$C$是容量-费用网络$N$中一条边不重复的回路，$E_C$是$C$的边集，$C$上的圈流$h^C$定义为：

$$h^C(i, j)=\begin{cases} \delta, & (i, j)\in E_C\\ 0, & otherwise \end{cases}$$

其中$\delta>0$称之为$h^C$的环流量。

显然，圈流是可行流，且$v(h^C)=0, w(h^C)=\delta\sum_{(i, j)\in E_C} w(i, j)$。简记$w(C)=\sum_{(i, j)\in E_C} w(i, j)$，$aw(C)$同理。

---

设$f$是$N$上的一个可行流，由引理，$f'=f+h^C$也是一个可行流，且$v(f')=v(f), w(f')=w(f)+\delta\cdot aw(C)$。

可以这样求最小费用流：首先求一个流量为$v_0$的可行流。如果$N_f$中存在$aw(C)<0$的负回路$C$，则可以令$f'\leftarrow f+h^C$（流量不变，费用减小），重复这个过程，直到$N_f$中不存在负回路为止。

9.3、最小费用流的负回路算法

（若干引理、定理待补充）

---

最小费用流的负回路的完整算法叙述如下：

1. 调用最大流算法。若求出的最大流流量小于$v_0$，无解，结束算法
2. 构造$N_f$
3. 用 Floyd 算法检测$N_f$中是否存在负回路，边的权函数是$aw$。若不存在负回路，返回当前$f$，结束算法
4. 令$\delta=\min\{ac(i, j)|(i, j)\in E_C\}$，然后更新流。具体而言：

   $$\begin{cases} f(i, j)\leftarrow f(i, j)+\delta, & (i, j)\in E_C\\ f(j, i)\leftarrow f(j, i)-\delta, & (j, i)\in E_C \end{cases}$$

   然后回到步骤 2

（待补充）

9.4、最小费用流的最短路径算法

另一种求最小费用流的思路是，从一个某个费用最小的初始流$f$开始（$v(f)<v_0$），然后寻找一条费用最少的 s-t 增广链，修改$P$上的流量，得到新的可行流$f'$。重复这个过程，直到流量达到$v_0$。

---

（若干引理、定理待补充）

---

最小费用流的最短路径算法的完整叙述如下：

1. 初始化零流$f$，当前流量$v=0$
2. 构造$N_f$
3. 调用 Floyd 算法，计算$N_f$中$s$到$t$的最短路径，权值函数为$aw$。如果不存在这样的路径，无解，结束算法；否则，记这条最短路径为$P$
4. 令$\theta=\min\{v, \min\{ac(i, j)|(i, j)\in E_P\}\}$，然后更新流。具体而言，对$E_P$中的每一条边$(i, j)$：

   $$\begin{cases} f(i, j)\leftarrow f(i, j)+\theta, & (i, j)\in E\\ f(j, i)\leftarrow f(j, i)-\theta, & (j, i)\in E \end{cases}$$

5. 令$v\leftarrow v+\theta$，如果$v\geqslant v_0$，结束算法；否则，回到步骤 2

10、运输问题

11、二部图匹配

11.1、定义

简单二部图是一个无向图$G=(A, B, E)$，其中$A, B$都是顶点集，边集满足$\forall (i, j)\in E, i\in A, j\in B$。

如果存在一个边集$M\subset E$，使得$M$中的边两两不相邻（不相邻即指没有公共顶点），则称$M$是$G$的一个匹配。边数最多的匹配称为最大匹配。当$|A|=|B|=|M|$时，称$M$是一个完美匹配。

---

设$M$是二部图$G$的匹配，称$M$中的边为匹配边，$E-M$中的边为非匹配边。与匹配边关联的顶点称为饱和点，不与任何一条匹配边关联的顶点称为未饱和点。

$G$中，由匹配边和非匹配边交替构成的路径称为交错路径。如果交错路径的起点和终点都是未饱和点，则称这条交错路径是增广交错路径。

---

引理：设$M$是二部图$G$的一个匹配，$P$是一个增广路径，则：

$$M'=M\oplus E_P=M\cup E_P-M\cap E_P$$

是一个匹配，且$|M'|=|M|+1$。其中$E_P$代表路径$P$上的边。

定理：二部图的匹配是最大匹配当且仅当不存在关于它的增广交错路径。

11.2、匈牙利算法

由上述定理，可以得到匈牙利算法的基本思想：从初始匹配$M$开始，不断寻找增广交错路径$P$，然后令$M\leftarrow M\oplus E_P$，直到不存在增广交错路径为止。

若$(A_i, B_j)\in M$，则记$match(A_i)=B_j, match(B_j)=A_i$。若$A_i$是未饱和点，则$match(A_i)=0$。

---

匈牙利算法的完整叙述如下：

1. 初始化匹配$M=\emptyset$
2. 记$A$中已标号未检查的点集为$X$，初始化$X=\emptyset$
3. 对于$A$中所有未饱和点$A_i$，给其打上标记$l(A_i)=0$，并将其加入$X$
4. 记$B$中未标号顶点集为$Y$，初始化$Y=B$
5. 当$X$非空时，从$X$中取出一个顶点$A_i$，对于$Y$中$A_i$的每一个邻接点$B_j$（也即$B$中与$A_i$邻接且未标记的点），取出，先给$B_j$打上标记$l(B_j)=A_i$：
   • 如果$B_j$是未饱和点，说明找到了一条增广交错路径，转到步骤 7
   • 如果$B_j$是饱和点，找到$B_j$对应的匹配点$A_k$，将$A_k$加入$X$，同时给$B_j$打上标记$l(A_k)=B_j$
6. $X$为空，没有找到增广交错路径，返回当前$M$，结束算法
7. 令$match(A_i)=B_j, match(B_j)=A_i$
8. 如果$l(A_i)=0$，说明到达起点，清空所有标记，回到步骤 2；否则，令$B_j\leftarrow l(A_i), A_i\leftarrow l(B_j)$，回到步骤 7

---

定理：匈牙利算法终止时得到的匹配是$G$的最大匹配，且算法在$O(\min\{|A|, |E|\}\cdot |E|)$时间内终止。

（证明待补充）