编译原理笔记

此份笔记是本人学习过程中自己总结记录的，其内容受到课堂教学内容、采用教材、个人认知水平的影响。虽然笔者力图保证内容准确以及易于理解（起码自己能看懂），但难免存在谬误或者渲染问题。非常欢迎您通过邮件等方式联系我修改，让我们一起让这份笔记变得更好！

第一讲 概论

编译器（Compiler）是一个系统软件。

---

一份 C 语言源代码变为可执行文件的过程如下：

1. 预处理阶段（Preprocessing）：汇合源程序，展开宏定义，生成 .i 文件
2. 编译阶段（Compiling）：将预处理后的文件翻译成汇编代码，生成 .s 文件
3. 汇编阶段（Assembling）：将汇编代码翻译成机器码，生成 .o 文件
4. 链接阶段（Linking）：链接成库代码，生成可执行文件

---

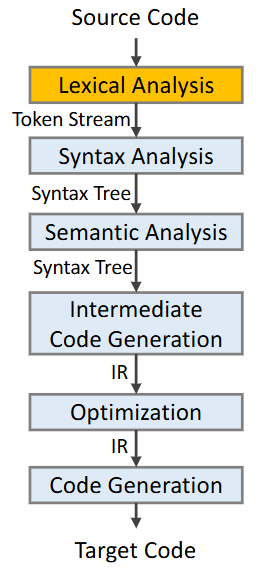
编译过程首先分为两个大阶段——前端和后端，具体如下：

• 前端：对源代码进行分析（Analysis），识别语法结构信息、理解语义信息、反馈错误，包括以下三个部分
  • 词法分析（Lexical Analysis）
  • 语法分析（Syntax Analysis）
  • 语义分析（Semantic Analysis）
• 后端：综合（Synthesis）前端的信息，最终生成目标机器代码，包括以下三个部分
  • 中间代码生成（Intermediate Code Generation）
  • 代码优化（Optimization）
  • 目标代码生成（Code Generation）

---

词法分析，将源代码视为文本/字符流，扫描，然后识别、分解出有词法意义的单词或符号（称之为 token）。

其输入为源代码，输出为 token 序列。每一个 token 可以由<type, attribute-value>的形式表示，token 的类型包括关键字、标识符、常量、运算符等。

在这一步中，还会检查 token 是否符合词法规则。例如 C 语言中的变量名是有一定规则的，不能以数字开头。

---

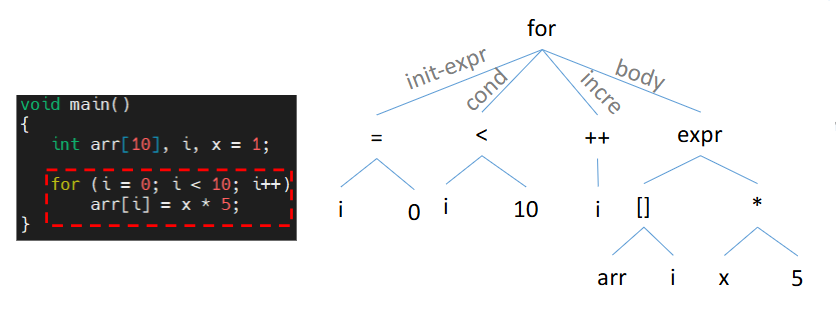
语法分析，会解析上一步得到的 token 序列，生成语法分析结构——语法树（Syntax Tree）。一个语法树的示例如下：

这一步还会检查，程序是否符合语法规则。例如语句必须以分号结尾。

---

语义分析，基于语法树进一步分析语义，得到符号表，同时会收集标识符的属性信息，例如类型、作用域等。

这一步还会检查，程序是否符合语义规则。例如 C 语言中，一个变量在使用之前必须先声明，且不能重复声明。

---

中间代码生成，根据语法树生成源程序的等价的中间表示（Intermediate Representation，IR）。IR 通常三地址码（Three Address Code）的形式，每条语句最多包含三个操作数。例如 a = b + c。

代码优化，对 IR 进行优化，使其更短/性能更高/内存使用更少。例如识别重复的运算，利用已知量替换未知量等。

目标代码生成，利用优化后的 IR 生成目标代码（例如汇编）。这一步中，要分配寄存器，选取恰当的指令实现 IR 中的操作。

第二讲 语言和文法基础

1、语言和文法的直观概念

程序设计语言包括语法和语义：

• 语法（Syntax）：是一组规则，根据可以构造出一个合法的程序。
• 语义（Semantics）：其定义了程序的意义，包括
  • 静态语义：程序在语义上要遵守的规则（在语法的基础之上的附加规则），例如数组下标不能越界，变量必须先声明等
  • 动态语义：表明程序要做什么

---

当语言是有穷的时候，可以把所有可能的句子列举出来。如果语言是无穷的，就要用某种方法来描述如何生成合法的语言中的句子。

文法（Grammar）是一种描述语言的语法的工具，利用有穷的规则描述出无穷的句子集。文法涉及符号、规则等概念，接下来会逐步介绍。

2、符号、符号串、符号串集合

字母表（Alphabet）是元素的非空有穷集合，一般用$\Sigma$表示。元素也称之为符号，字母表也称之为符号集。程序语言的字母表由英文字母、数字以及若干个专用的符号组成。

---

符号串（String）是由字母表中的符号组成的任何有穷序列（有顺序的）。不含任何符号的符号串称之为空串，用$\varepsilon$来表示。符号串的长度是符号串中符号的个数。

符号串的：

• 头：也即前缀，从头开始连续若干符号构成的子串，包括空串。
• 尾：也即后缀，从尾开始连续若干符号构成的子串，包括空串。
• 固有头：也即真前缀，除原符号串和空串之外的头。
• 固有尾：也即真后缀，除原符号串和空串之外的尾。

---

符号串的运算：

• 连接运算：设$x$和$y$是符号串，则$xy$就是它们的连接，结果是两个符号串的拼接。注意$xy$和$yx$是不同的。
• 方幂运算：设$a$是符号串，$a^n$即是其$n$次幂，结果是$a$自身连接$n$次$aaaa\cdots a$

---

若集合$A$中的所有元素都是某个字母表$\Sigma$上的符号串，则称$A$为$\Sigma$上的符号串集合。

符号串集合$A$和$B$的乘积定义为$AB=\{xy|x\in A, y\in B\}$

符号串集合的方幂定义为$A^n=AAAA\cdots A$，特别地$A^0=\{\varepsilon\}$

3、闭包和正闭包

集合$\Sigma$的闭包（Closure）$\Sigma^*$定义如下：

$$\Sigma^*=\Sigma^0\cup\Sigma^1\cup\Sigma^2\cup\cdots$$

也即$\Sigma$上所有有穷串的集合。

正闭包定义为$\Sigma^+=\Sigma^1\cup\Sigma^2\cup\cdots$，也即$\Sigma$上除空串之外的所有有穷串的集合。显然有$\Sigma^*=\Sigma^+\cup \Sigma^0$，$\Sigma^+=\Sigma\Sigma^*= \Sigma^*\Sigma$。

4、文法

文法（Grammar）是一个四元组$G=(V_N,V_T,P,S)$，其中：

• $V_N$是非终结符集合（Non-terminal Set）
• $V_T$是终结符集合（Terminal Set）
• $P$是产生式集合（Production Set），也即规则集合
• $S$是开始符号（Start Symbol）

其中$V_N, V_T, P$都是非空的有穷集合。$V=V_N \cup V_T$称为文法$G$的字母表。

还要满足$V_N \cap V_T = \emptyset$，也即一个符号不能同时是终结符和非终结符。

$S\in V_N$，也即开始符号是一个非终结符，且至少要在一条产生式的左边出现。

---

产生式，或者说规则是一个符号串的有序对$(\alpha, \beta)$，通常写为$\alpha \rightarrow \beta$或者$\alpha ::= \beta$。其中$\alpha\in V^+$（不能为空串）且至少包含一个非终结符，$\beta\in V^*$。

$\alpha \rightarrow \beta$的意思是，$\alpha$可以被替换为$\beta$，也即$\alpha$可以推导出$\beta$。

例如汉语的一条规则就可以写为<句子> ::= <主语> <谓语>。

---

为了简化文法的表示，通常不写出整个四元组，只写出产生式集，同时做以下约定：

• 第一条产生式的左部的符号是开始符号，或者换用来$G[S]$文法，其中$S$就是开始符号
• 用大写字母表示非终结符（或者用尖括号括起来），用小写字母表示终结符
• 左部相同的产生式可以合并，不同的右部用|分隔。例如$A\rightarrow a, A\rightarrow b$可以写为$A\rightarrow a|b$

---

若$\alpha\rightarrow \beta$是文法$G$的一个产生式，且$v, w$满足$v=\gamma \alpha \delta. w=\gamma\beta\delta$，其中$\gamma, \delta\in V^*$，则称$v$可以（应用这一条产生式）直接推导出$w$，记作$v\Rightarrow w$。或者说$w$可以直接归约到$v$。

若存在$v=w_0\Rightarrow w_1\Rightarrow w_2\Rightarrow\cdots\Rightarrow w_n=w(n>0)$，则称$v$可以推导出$w$，记作$v\Rightarrow^+ w$。或者说$w$可以归约到$v$。

如果有$v\Rightarrow^+ w$（通过至少一步推导），或$v=w$（0 步推导），则记为$v\Rightarrow^* w$（非负步数推导）。这与闭包和正闭包的定义和记号是类似的。

5、句型、句子、语言

对于文法$G[S]$，由开始符号$S$推导能够得到的符号串$\alpha$（也即$S\Rightarrow^* \alpha$），称之为文法$G[S]$的句型

仅由终结符组成的句型$\alpha$，也即$S\Rightarrow^* \alpha, \alpha\in V_T^*$，称之为文法$G[S]$的句子。后续，句子都以小写希腊字母如$\alpha, \beta, \gamma$等表示。

文法$G[S]$所有句子的集合称之为文法的语言，记作$L(G)$。

如果$L(G_1)=L(G_2)$，则称文法$G_1$和$G_2$是等价的。

6、文法的类型

根据产生式满足的限制，Chomsky 将文法分为四种类型：

• 0 型文法（短语文法）
• 1 型文法（上下文有关文法）
• 2 型文法（上下文无关文法）
• 3 型文法（正规文法）

---

若文法$G$的任意产生式$\alpha\rightarrow \beta$都满足$\alpha\in V^+$且至少包含一个非终结符， $\beta \in V^*$，则称文法$G$是0 型文法。

这个定义与原来文法的定义完全相同，也就是说任何文法都是 0 型文法。

---

若文法$G$的任意产生式$\alpha\rightarrow \beta$（除了$S\rightarrow \varepsilon $之外）都满足$|\beta| \geqslant |\alpha|$，则称为**1 型文法**。1 型文法是 0 型文法的特例，在 0 型文法的基础上，增加了$|\beta| \geqslant |\alpha|$的限制。

根据定义，可以写出 1 型文法产生式的一般形式$\alpha A \gamma \rightarrow \alpha \beta\gamma$，其中$\alpha, \gamma\in V^*$，$A\in V_N$，$\beta\in V^+$。可以理解为，非终结符$A$的上文和下文分别为$\alpha$和$\gamma$时，可以把$A$替换为$\beta$，所以 1 型文法也称之为上下文有关文法（Context-sensitive Grammar）。

---

若文法$G$的任意产生式$\alpha\rightarrow \beta$都满足$\alpha\in V_N$，则称为2 型文法。2 型文法是 1 型文法的特例，在 1 型文法的基础上，增加了$\alpha\in V_N$的限制，也即产生式的左边一定是单个的非终结符。

所以可以写出 2 型文法产生式的一般形式$A\rightarrow \beta$。可以理解为，只要看见非终结符$A$，就可以被替换为$\beta$。与 1 型文法相比，不用关心$A$的上下文，所以 2 型文法也称之为上下文无关文法（Context-Free Grammar，CFG）。

通常程序设计语言的文法都是 2 型文法。

---

若文法$G$的任意产生式$\alpha\rightarrow \beta$的形式都是$A\rightarrow aB$或$A\rightarrow a$，其中$A, B\in V_N$，$a\in V_T$，则称为3 型文法。可以看出，3 型文法是 2 型文法的特例，在 2 型文法的基础上，增加了产生式的右部只能是终结符或者终结符加一个非终结符的限制。

程序设计语言中，3 型文法通常用于描述单词的结构。

7、上下文无关语法以及语法树

7.1、规范推导和规范句型

如果在推导的任何一步，例如正要对$\alpha\rightarrow \beta$进行推导，总是对$\alpha$中最左边的非终结符进行替换，则称这种推导为最左推导。同理，如果总是对最右边的非终结符进行替换，则称为最右推导。

最右推导又称之为规范推导。通过规范推导得到的句型称之为规范句型，也称为右句型。

---

任意的句型推导过程都可以写为推导树（Parse Tree，也称为语法树）的形式，形如：

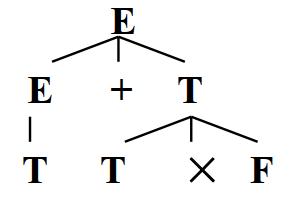
从语法树中，看不出推导过程中符号被替换的顺序。最后从左往右读出叶子结点得到的符号串，就是文法的一个句型，也即语法树对应的推导过程得到的最终结果。

语法树的正式定义为：给定文法$G=(V_N,V_T,P,S)$，若一棵树满足：

• 每个节点都有一个标记，且标记是$V$中的一个符号
• 根节点的标记是开始符号$S$
• 若有一个节点至少有一个子节点，且标记为$A$，则一定有$A\in V_N$
• 如果节点$n$有标记$A\in V_n$，其直接子节点从左往右的标记依次为$A_1, A_2, \cdots, A_k$，则一定有$A\rightarrow A_1A_2\cdots A_k$一定是$P$中的一个产生式

就称这棵树是文法$G$的一个语法树。

7.2、文法的二义性

如果一个文法存在某个句子可以有两棵不同的语法树（有两个不同的最左/右推导），就称这个文法是二义的。

任何一个二义性的文法都可以转换为一个等价的无二义性文法。

8、句型分析

句型分析，就是识别一个符号串是否是文法的一个句型。如果能够根据文法构造出该符号串的语法树，则该符号串就是该文法的一个句型。

句型分析的算法包括自上而下分析和自下而上分析两种。

---

自上而下分析方法，就是从开始符号开始，尝试推导出符号串。显然，这种方法存在问题，对于某一个中间状态，可能有多种替换方式。如果替换错误，就有可能得不到正确的句型。

自下而上分析方法，就是从符号串开始，尝试归约到开始符号，与自上而下分析法过程相反。这种方法仍然存在类似的问题，对于某一个中间状态，可能有多种归约方式。

---

自下而上的分析方法中，每一步都是从当前串中选择一个子串进行规约，这个子串称之为可规约串。要想成功的进行句型分析，就是要确定每一步的可规约串。

设$\alpha \beta \delta$是文法的一个句型，如果有$S\Rightarrow^* \alpha A\delta$，且$A\Rightarrow^+ \beta$，则称$\beta$是句型$\alpha\beta\delta$相对于非终结符$A$的一个短语（Phrase）。特别的，如果有$A\Rightarrow \beta$，就称$\beta$是句型$\alpha\beta\delta$相对于规则$A\rightarrow \beta$的一个直接短语（或者说简单短语）

一个句型的最左边的直接短语，称为该句型的句柄（Handle），句柄显然是一个可规约串。

---

从句型的语法树上，容易找出句型的短语。语法树中：

• 每棵子树的末端结点就构成相对于子树的根的短语。

• 只有两层的子树得到的短语是直接短语。

• 最左边的只有两层的子树得到的短语，是句柄。

9、有害规则和无害规则

有害规则，例如$U\rightarrow U$，是无用的，且会引起文法的二义性

多余规则，所有句子的推导中都用不到的规则，包括：

• 不可到达：该规则左部的非终结符不在任何规则的右部出现
• 不可终止：使用该规则后，无法推导出句子

---

为了避免有害规则和多余规则

• 规则中的任意终结符 A 必须在某句型中出现，也即有$S\Rightarrow^* \alpha A\beta$，其中$\alpha, \beta\in V^*$
• 必须能够从$A$推导出一个句子，也即有$A\Rightarrow^* \gamma$，其中$\gamma\in V_T^*$

---

特别地，在上下文无关文法中，允许使用规则$A\rightarrow \varepsilon$，其中$A$是非终结符。这种规则称为空规则（Null Rule）。

第三讲 词法分析

1、概述

之前已经提到，词法分析就是扫描源程序字符流，识别并分解出有词法意义的单词或符号，也即将字符流变成 token 序列。

词法分析器根据其要完成的工作，也称为扫描器（Scanner）或者 Tokenization。词法分析器要处理的问题包括：

• 移除注释
• 识别 token
• 确认 token 所属的类别

后续根据 token 的类别信息进一步进行语法分析等。

---

Token，词，是最小的有词法意义的单元。编程语言中常见的 token 类别包括关键字、标识符、常量、运算符、标点符号等。

某个 token 类别的一个实例称之为词素（Lexeme）。

---

实现词法分析的过程中还需要注意一些问题：

• 要识别并丢弃无意义的词，包括空白字符、注释等
• token 的类别可能存在二义性，可能需要查看上下文来确定，有时候还需要 parser 的反馈。但是，应该尽量减少“前后看”的次数。

2、词法规范

词法规范（Lexical Specification）是描述 token 的类别以及如何识别 token 的规则。词法规范包括三种：

• 表达式：包括正则表达式和正则定义
• 文法：正规文法
• 有穷自动机：包括确定的有穷自动机和非确定的有穷自动机

2.1、正则表达式

正则表达式（Regular Expression，RE）可以用于定义 token 类别。

正规式也即正则表达式，定义了某种字符串模式。正规式表示的正规集，则是满足该正规式的所有字符串的集合。

对于任意的$a\in \Sigma$，$a$是$\Sigma$上的一个正规式，其表示的正规集为$L(a)=\{a\}$。特别地，空串$\varepsilon$也是正规式，其表示的正规集$L(\varepsilon)=\{\varepsilon\}$；空集$\emptyset$也是正规式，其表示的正规集$L(\emptyset)=\emptyset$

假定$r, s$均为$\Sigma$上的正规式，它们所表示的正规集分别为$L(r), L(s)$，则以下也是正规式以及表示的正规集：

• 正规式$(r)$，表示的正规集$L((r))=L(r)$
• 正规式$r|s$，表示的正规集$L(r|s)=L(r)\cup L(s)$
• 正规式$r\cdot s$，表示的正规集$L(r\cdot s)=L(r)\cdot L(s)$
• 正规式$r^*$，表示的正规集$L(r^*)=(L(r))^*$

利用上面提及的算符进行有限次运算得到的式子才是正规式。算符的优先级顺序是() > * > . > |，其中连接和或都是左结合的。

---

|算符满足交换律和结合律：$r|s=s|r, r|(s|t)=(r|s)|t$

|算符还满足抽取律：$r|r=r$

.算符满足结合律和分配律：$(r\cdot s)\cdot t=r\cdot(s\cdot t), r\cdot (s|t)=r\cdotp s|r\cdot t, (r|s)\cdot t=r\cdot t|s\cdot t$

---

为了简化表达，在不引起歧义的情况下，还可以有以下形式的正规式：

• $A^+$，等价于$A\cdot A^*$，也即表示至少有一个$A$
• $A?$，等价于$A|\varepsilon$，也即表示有一个或者没有$A$
• $[a_1a_2\cdots a_n]$，等价于$a_1|a_2|\cdots|a_n$。特别地，对于英文字母，$[a-z]=[abcd\cdots z]$。$[\ \^{}\ a-z]$表示除了$a|b|\cdots|z$之外的字符

正规式相比正规文法更简洁易懂，而且由正规式可以自动地构造出识别程序。

3、有穷自动机

转换图（Transition Diagram）是一个有向图，其节点（用圆圈表示）代表状态，边（用箭头表示）代表状态之间的转移，转换图的每个边上都有一个标记。

为了方便指代，通常会给每个状态/节点一个序号。若状态$A$和状态$B$之间，有一个带$x$标记的边，简记为$(A, x)\rightarrow B$。由于状态本身的标记并不重要，所以可以任意的重命名状态。这也是后面将 NFA 转为 DFA 时，可以合并状态的理论基础。

初始状态（Start/Initial State）只有一个，有一条没有源节点的入边指向它。终止状态（Accepting/Final States）可以有多个，用双圆圈表示。

词法分析器从初始状态开始，根据输入的字符，沿着转换图的边进行转移，直到到达终止状态。如果到达终止状态，就识别出一个 token。

---

自动机（Automata）是一个机器或者程序，有穷自动机（Finite Automata，FA）基于转换图，其状态是有限的。

之前的正则表达式是对词法规则的定义，自动机则是根据规则识别 token 的实现。FA 是一个对字符串进行分类的程序，对任意字符串，给出“接受”或者“拒绝”的分类结果。对于给定的字符串 $x$ ，如果存在一条从 FA 的初始结点到某一个最终结点的通路，且该通路上所有边上的符号连接成的字符串等于 $x$，则称 $x$ 可被 FA 识别，或称 $x$ 被 FA 接受。

FA 的形式化定义为一个五元组 $M=(S, \Sigma, \delta, s_0, F)$，其中：

• $S$ 是有穷的状态集
• $\Sigma$ 是输入字母表
• $\delta$ 是状态转移函数，$\delta: S\times \Sigma \rightarrow S$，对每个状态以及输入符号，$\delta$ 给出下一个状态
• $s_0\in S$ 是初始状态
• $F\subseteq S$ 是终止状态集

---

DFA（Deterministic Finite Automaton，确定有穷自动机）在任意时刻，只能以一种状态存在。DFA 中每个状态对于每个输入只有一个转移，也即对 DFA，有$\delta: S\times \Sigma \rightarrow S$。DFA 中，没有$\varepsilon$转移。

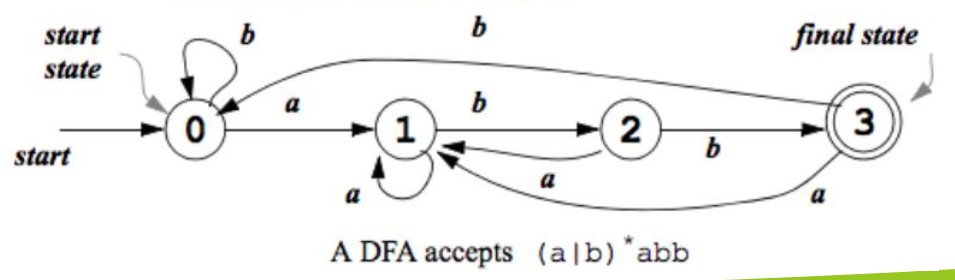
NFA（Non-deterministic Finite Automaton，非确定有穷自动机）在某一时刻，可以以多种状态存在。NFA 中每个状态对于每个输入可以有多个转移，也即对 NFA，有$\delta: S\times \Sigma \rightarrow 2^S$。NFA 中，可以有$\varepsilon$转移。对于 $\varepsilon$-NFA，有$\delta: S\times (\Sigma\cup \{\varepsilon\}) \rightarrow 2^S$

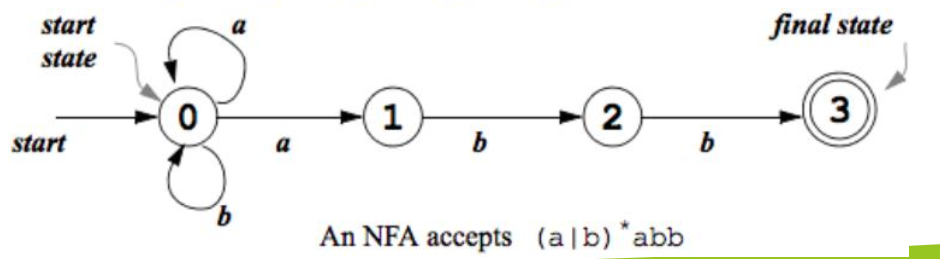
对于 DFA，一个字符串在转换图上只可能有一条路径。对于 NFA，一个字符串可能有多条路径，但是只要有任意一条路径可以到达终止状态，就认为这个字符串被 NFA 接受。

4、转换和等价

从抽象的词法规则，到具体的词法分析器程序，其流程如下：

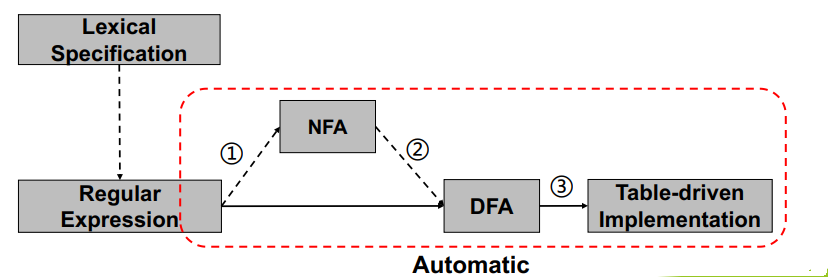
4.1、RE 到 NFA

RE 到 NFA 采用 Thompson 构造算法，输入为对于字母表$\Sigma$上的一个正规式 $r$，输出是一个 接受$L(r)$的 NFA。其基本的思想是，分析$r$，从其最小的子部分开始构造 NFA，然后逐步合并。

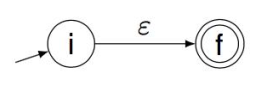
1. 处理原子正规式。例如对于 $\varepsilon\in \Sigma$，需要添加初始和终止两个状态，然后一个$\varepsilon$转移：
   
2. 处理组合正规式
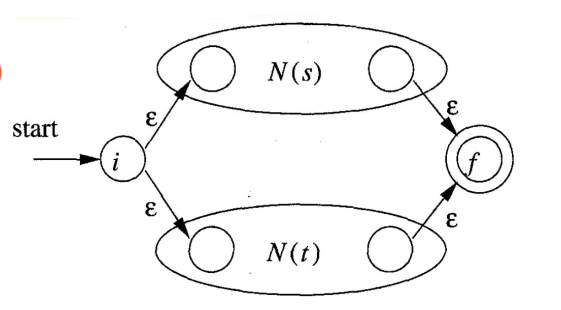
   • 对于$r=s|t$，增加两个新的状态，以及 4 个$\varepsilon$转移：
     
   • 对于$r=st$，无需增加新的状态和转移：
     
   • 对于$r=s^*$，增加两个新的状态，以及 4 个$\varepsilon$转移：
     

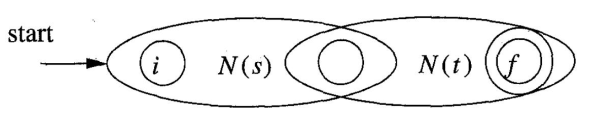
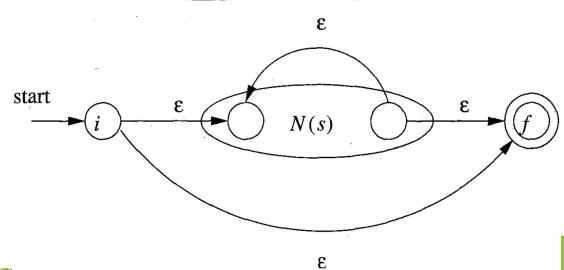
注意，这里$N(s)$或$N(t)$中的两个圆圈，分别指向了$N(s)$或$N(t)$的初始状态和终止状态。两个圆圈重叠表示合并，也即$N(s)$的终止状态就是$N(t)$的初始状态。

4.2、NFA 到 DFA

NFA 的转移是不确定的，难以用机器模拟，所以要将 NFA 转换为 DFA。对于每一个 NFA，都存在一个与其等价的 DFA。

---

$\varepsilon$-NFA 到 DFA 的转换可以使用$\varepsilon$-闭包算法。状态集合$I$的$\varepsilon$-闭包是指，$I$中的任意状态经过任意次（包括 0 次）$\varepsilon$转移能到达的状态的集合：

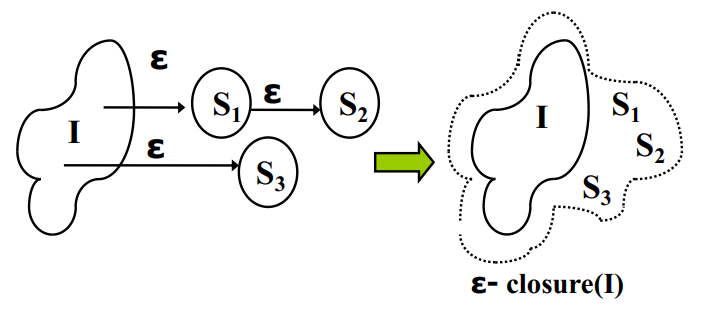
$\varepsilon$-闭包算法的具体流程如下：

• 计算$\{s_0\}$的$\varepsilon$-闭包，记为$A$
• 遍历字母表，对于每个字母$a$，计算$A'$的$\varepsilon$-闭包，记为$B$。其中$A'=\{y|(x, a)\rightarrow y, x\in A\}$。
• 重复上一步，直到没有新的状态集合产生。将$A, B, \dots$视为状态/节点，构造出 DFA。

同一个状态集中的状态，是从开始状态经过完全相同的输入符号序列（$\varepsilon$可以忽略）能够转移到的，所以是完全等价的，可以用一个状态/节点来表示。

---

普通 NFA 到 DFA 的转换可以使用子集构造算法。

子集构造算法通过建立状态转移矩阵来进行。例如下面是一个 NFA 以及其状态转移矩阵：

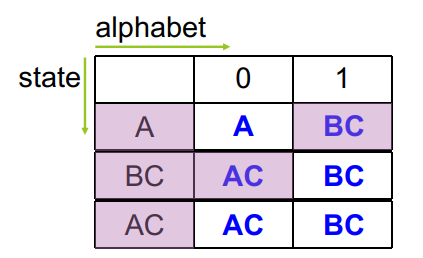
出现新的状态集时，就给转移矩阵增加一行，然后遍历字母表，产生新的状态集，填充到各个列中。直到没有新的状态集产生，然后画出 DFA。

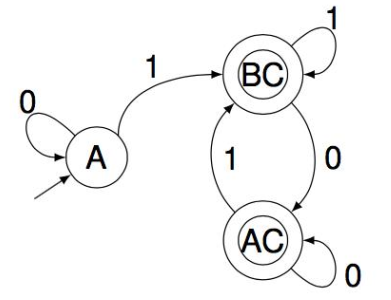
为了简便，可以对重命名。例如矩阵中的 AC 可以重命名为 D，当作 DFA 中的一个节点。

4.3、DFA 化简

DFA 化简的目的是去除多余状态以及合并等价状态：

• 多余状态：指从开始状态无论如何都无法到达的状态
• 等价状态：当两个状态满足下面两个条件时，认为是这两个状态是等价的：
  • 一致性条件：两个状态都是终止状态或者非终止状态
  • 蔓延性条件：对于所有的输入符号，两个状态都能够转移到等价的状态

例如上面的例子中，AC 和 BC 是等价的，可以合并：

---

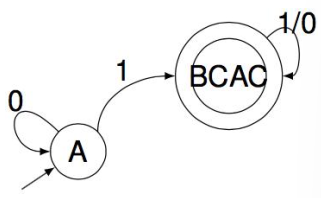
若一个状态集中的所有状态时等价的，称这个状态集是等价集。

DFA 化简的基本思路就是，一开始将所有符号放到一个集合中，视为一个“等价集”，然后根据状态转移图，不断分割这个集合，知道每个集合变成真正的等价集。具体流程如下：

1. 初始化，构造两个集合，一个是终止状态集合，一个是非终止状态集合。这两个集合都视为“等价集”。
2. 观察状态转移图，若同一个“等价集”中的两个状态在某个输入符号下，转移到了不属于同一个“等价集”的状态，就将这两个状态分开。反之，则合并这两个状态。
3. 重复上一步，直到无法继续分割或合并。

4.4、DFA 到 Table-Drive Implementation

根据 DFA，可以画出二维状态转移矩阵Table，其中行表示状态，列表示输入符号，每个元素表示下一个状态。然后可以根据这个表格，写出词法分析器的伪代码：

DFA(){
  start='s0';
  while(!done){
    ch = nextChar();
    state=Table[state][ch];
    if (start=='x') // 不存在这样的转移
      return "reject";
  }
  if(state in F)
    return "accept";
  else
    return "reject";
}

4.5、复杂度分析

Table-Drive Implementation 是一种高效的实现，其空间复杂度为$O(|S|\times |\Sigma|)$，时间复杂度为$O(X)$，其中$X$是输入字符串的长度。

在给定的状态和输入下，这种实现能够在$O(1)$内找到下一个状态。但是，当状态数较多或字母表很大时，就会需要很大的空间。

---

对于 NFA，假设输入长度仍然为$X$，每一步可能有$O(N)$个状态，这$O(N)$个状态的每一个，都可能转移到$O(N)$个状态，所以 NFA 每一步需要花费$O(N^2)$的时间。则 NFA 的时间复杂度为$O(N^2X)$，远远高于 DFA。

5、词法分析器的实现

实际编写一个词法分析器时，我们只需要编写正则表达式以及相应的动作（lex.l），工具会根据我们编写的规则，自动生成能够按此规则识别 token 的源代码（lex.yy.c），暴露出供我们调用的函数(yylex())。我们只需要在主程序中，接收输入，并调用函数处理，即可得到结果。以上，就完成了词法分析的过程。

对于我们编写的每一个正则表达式，都对应着一个 DFA。首先会引入一个新的状态和若干个$\varepsilon$转移，将这些 DFA 合并为一个$\varepsilon$-NFA，再经过一系列转换之后，变为 Table-Drive Implementation。

---

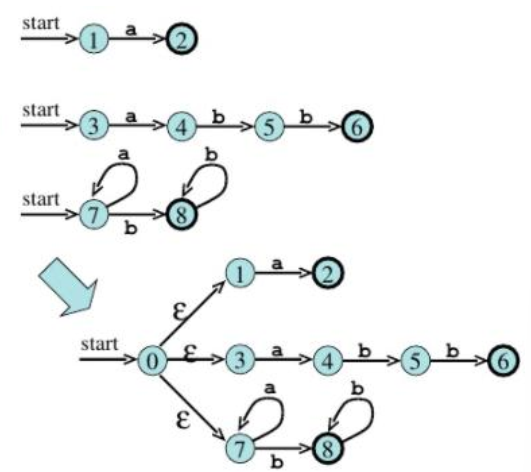
当存在多种可能的匹配时，首先采取最长匹配原则，如果还存在多种匹配，则取规则列表中先出现的规则。

例如，要识别关键字，可以为关键字单独写正则表达式，并放在标识符的正则表达式之前。由于优先级更高，会先识别关键字。这样会导致 FA 更加复杂。

另一种方法是，不单独写正则表达式，标识符和关键字一起匹配。但是额外引入关键字表，匹配的字符串要再次查找关键字表，判断是否是关键字。这样 FA 更简单，但是需要额外的表。这种方法是更常见的。

第四讲 语法分析

语法分析根据 token 序列，生成语法树，同时要检查输入是否符合语法规则。

本讲中，我们主要的研究对象是上下文无关文法，其产生式的一般形式是$A \rightarrow \beta$，也即产生式的左部总是单个的非终结符。若没有特别说明，接下来的“文法”指的都是“上下文无关文法”。

1、自顶向下分析

之前在句型分析中，我们提到了自顶向下分析，由开始符号开始，尝试推导出句型，这个过程中构建出语法树。我们还提到，文法可能具有二义性，也即对于同一个句子/句型，可能有多个语法树（或者说多个最左/最右推导）。

1.1、推导过程确定的文法

设文法$G[S]$，若：

• 每个产生式的右部，都以终结符开头
• 左部相同的产生式，其右部开头的终结符互不相同

则在我们推导某个句子时（全由终结符构成），推导过程是唯一确定的。考虑开始推导时，指针指向目标串的开头。在遍历过程中，我们总是能根据指针当前指向的符号（一定是终结符），唯一确定一个产生式。

---

而实际我们遇到的文法中，不一定能完美满足上面的条件。例如：

• 左部相同的产生式，其中存在两条产生式，其右部的第一个终结符相同，或者说存在左公因子，则在推导过程中，无法确定使用哪一个产生式。
• 指针是从左向右遍历的，假如使用某个产生式后，唯一可用的产生式还是这个，陷入无限循环。这种产生式称为是左递归的，例如$E\rightarrow E+T$，其左部和右部的第一个符号是相同的非终结符。
• 文法存在二义性，天然就会导致多种推导方式。

我们希望消除这些问题，使得推导过程唯一确定。

---

消除左公因子。

提取出左公因子，并引入一个新的非终结符。

例如，产生式$A\rightarrow \alpha\beta_1 | \alpha\beta_2 | \dots | \alpha \beta_n$，则可以提取左公因子得到$A\rightarrow \alpha(\beta_1| \beta_2\dots|\beta_n)$，然后引入新的非终结符$A'$，拆成两条产生式$A\rightarrow \alpha A', A'\rightarrow \beta_1| \beta_2\dots|\beta_n$。如果$\beta_1| \beta_2\dots|\beta_n$中还存在左公因子，可以继续提取。

本质是把做决定的时间往后延，把确定能够唯一匹配的部分先匹配出来。

---

消除左递归。

引入新的非终结符进行改写。

例如，产生式$A\rightarrow A\alpha_1 | A\alpha_2 | \dots | A\alpha_m | \beta_1 | \beta_2 | \dots | \beta_n$，则引入新的非终结符$A'$，得到$A\rightarrow \beta_1A' | \beta_2A' | \dots | \beta_nA', A'\rightarrow \alpha_1A' | \alpha_2A' | \dots | \alpha_mA' | \varepsilon$。这样就消除了左递归。这样将左递归变为了右递归，且引入$\varepsilon$，显式终止递归。

对于直接左递归，例如$E\rightarrow E+T$，可以直接利用上面的方法消除。

对于间接左递归，例如$S\rightarrow Qc|c, Q\rightarrow Rb|b, R\rightarrow Sa|a$。其基本思想是先将间接左递归转为直接左递归，再用上面的方法消除。具体步骤如下：

• 将文法的所有非终结符按任一顺序排列，如$A_1, A_2, \dots, A_n$
• 从左到右遍历这个排列。对于$A_i$，考虑左部为$A_i$的产生式，如果其右部以$A_j(j<i)$开头，也即$A_i\rightarrow A_j\alpha$，则将左部为$A_j$的产生式代入其中（就类似于解多元一次方程组时进行消元操作）。重复这个过程，直到没有产生式的右部以某个$A_j(j<i)$开头。如果最后的结果存在左递归，则将其消除。
• 去掉无用产生式（无法到达的产生式）

根据一开始排列的顺序不同，可能会得到不同的结果。但是，这些结果都是等价的。

例如上面的例子中，原来的三个产生式，按照$R, Q, S$的排列，最终变为$S\rightarrow abcS' | bcS' | cS', S'\rightarrow abcS' | \varepsilon$。如果按照$S, Q, R$的排列，则最终变为$S\rightarrow Qc|c, Q\rightarrow Rb|b, S\rightarrow bcaR'|caR'|aR', R'\rightarrow bcaR'|\varepsilon$。

---

消除二义性。

一个典型的例子是悬空 else 问题（Dangling-else Problem）。假如有产生式stmt -> if expr then stmt | if expr then stmt else stmt | other，则对于输入if expr1 then if expr2 then stmt1 else stmt2，存在两种解释：

• stmt -> if expr1 then (if expr2 then stmt1) else stmt2
• stmt -> if expr1 then (if expr2 then stmt1 else stmt2)

消除二义性可以通过引入额外的规则，例如限定“每个else只能与最近的尚未匹配的then匹配”。另一种做法是，将原文法改写为等价的无二义性文法。

例如，用matched_stmt代表完整的if-then-else语句，open_stmt代表没有else的if-then语句。规定then和else之间，只能是matched_stmt。

• stmt -> matched_stmt | open_stmt
• matched_stmt -> if expr then matched_stmt else matched_stmt | other
• open_stmt -> if expr then stmt | if expr then matched_stmt else open_stmt

则对于原来的输入，就只有stmt -> if expr1 then (if expr2 then stmt1 else stmt2)一种理解了。

---

消除$\varepsilon$产生式。

$\varepsilon$产生式即形如$A\rightarrow \varepsilon$的产生式。$\varepsilon$产生式的存在可能会使推导过程变得复杂。

对于每个产生式，考虑其右部中的非终结符$X_i$，如果有$X_i\Rightarrow^+ \varepsilon$，则可以将$X_i$替换为$\varepsilon$，得到新的产生式。在同一个产生式中，这样的替换可以发生任意次。得到所有可能的产生式后，再将其中的$\varepsilon$产生式去掉。

例如对于产生式$S\rightarrow aSbS|bSaS|\varepsilon$，可以得到$S\rightarrow aSbS|aSb|abS|ab|bSaS|bSa|baS$。

1.2、FIRST 集

若一个文法中存在某个产生式，其右部不是以终结符开头，是否意味着推导过程不确定呢？答案是否定的。

---

例如下面这个文法：

$$\begin{align*} &S\rightarrow Ap|Bq \\ &A\rightarrow a|cA \\ &B\rightarrow b|dB \end{align*}$$

考虑输入串$W=ccap$，可以发现其推导过程仍然是确定的。输入串第一个符号是$c$，只可能使用$S\Rightarrow Ap \Rightarrow cAp$得到。可以发现，这里考虑了多步，而不是像之前那样只单纯看产生式（即只看一步）。

---

一般地，可以定义某个串$\beta, \beta\in(V_N \cup V_T)^*$的 FIRST 集：

$$\text{FIRST}(\beta)=\{a|a\in V_T, \beta\Rightarrow^* a\gamma\}$$

也即$\beta$能推出的所有以终结符开头的串的第一个符号的集合。特别地，若$\beta\Rightarrow^* \varepsilon$，则$\varepsilon\in \text{FIRST}(\beta)$。

如果左部相同的产生式的右部的 FIRST 集两两不相交，则推导过程是唯一确定的。

---

同时求文法中的所有符号$X\in V_T \cup V_N$的 FIRST 集的算法如下：

1. 一开始，所有符号的 FIRST 集都为空集
2. 若$X\in V_T$，则$\text{FIRST}(X)=\{X\}$。所有终结符的 FIRST 集已确定。
3. 若有产生式$X\rightarrow \varepsilon$，则$\text{FIRST}(X)\leftarrow \text{FIRST}(X)\cup \{\varepsilon\}$
4. 考虑产生式$X\rightarrow Y_1Y_2\dots Y_k$
   • 从左到右遍历$Y_i$。对于每个$Y_i$，如果$Y_i\Rightarrow^* \varepsilon$，则$\text{FIRST}(X)\leftarrow \text{FIRST}(X)\cup (\text{FIRST}(Y_i)-\{\varepsilon\})$
   • 直到遇到某个$Y_j$有$Y_j\not\Rightarrow^* \varepsilon$，则$\text{FIRST}(X)\leftarrow \text{FIRST}(X)\cup \text{FIRST}(Y_j)$
   • 如果不存在这样的$Y_j$，也即$Y_1Y_2\dots Y_k\Rightarrow^* \varepsilon$，则还要$\text{FIRST}(X)\leftarrow \text{FIRST}(X)\cup \{\varepsilon\}$
5. 重复第四步，直到所有符号的 FIRST 集不再变化

在实际操作的过程中，还有以下几点优化：

• 形如$A\rightarrow a \gamma, a\in V_T, \gamma\in(V_T \cup V_N)^*$的产生式，也可以在第四步之前就处理掉，然后划掉。这种产生式只会“起效”一次。
• 以某个非终结符为左部的所有产生式都被划掉，则这个非终结符的 FIRST 集就不再变化，已经确定了。
• 如果某个符号的 FIRST 集已求出，把这个符号称为是“已求出的”。右部全为“已求出的”符号的产生式，处理过一次后也可以直接划掉。

---

知道每个符号的 FIRST 集后，就可以确定所有符号串的 FIRST 集。设$\alpha=X_1X_2\dots X_n$，从左向右遍历$X_i$，如果$X_i\Rightarrow^* \varepsilon$，则$\text{FIRST}(\alpha)\leftarrow \text{FIRST}(\alpha)\cup (\text{FIRST}(X_i)-\{\varepsilon\})$，直到遇到某个$X_j$有$X_j\not\Rightarrow^* \varepsilon$，则$\text{FIRST}(\alpha)\leftarrow \text{FIRST}(\alpha)\cup \text{FIRST}(X_j)$。如果不存在这样的$X_j$，也即$X_1X_2\dots X_n\Rightarrow^* \varepsilon$，则还要$\text{FIRST}(\alpha)\leftarrow \text{FIRST}(\alpha)\cup \{\varepsilon\}$。

利用这个方法，求出所有产生式右部的 FIRST 集，就可以判断该文法的推导过程是否唯一确定了。

1.3、FOLLOW 集

考虑另一种有产生式的右部不是以终结符开头的文法，具体来说，是包含空产生式的文法。例如：

$$\begin{align*} &S\rightarrow aA|d \\ &A\rightarrow bAS | \varepsilon \end{align*}$$

考虑输入串$W=abd$，其推导过程也是唯一确定的。推导到$S\Rightarrow aA\Rightarrow abAS$后，我们怎么确定是要应用$A\rightarrow bAS$还是$A\rightarrow \varepsilon$呢？

这个时候，需要我们“往后看”一个字符，发现是$d$，而应用$A\rightarrow bAS$之后，是不可能推导出$d$的，只能调用$A\rightarrow \varepsilon$。

---

一般地，可以对于终结符$A$，可以定义其FOLLOW 集：

$$\text{FOLLOW}(A)=\{b\in V_T|S\Rightarrow^* \alpha Ab\beta\}$$

也即所有可能紧跟在$A$后面的终结符的集合。特别地，如果$S\Rightarrow^* \alpha A$，则$\$ \in \text{FOLLOW}(A)$，其中$\$$表示输入串的结束符。

如果所有产生式的非空右部的 FIRST 集和其左部的 FOLLOW 集两两不相交，则推导过程是唯一确定的。

---

求文法中所有非终结符的 FOLLOW 集的算法如下：

1. 一开始，所有非终结符的 FOLLOW 集都为空集。 显然$S\Rightarrow^* S$，所以$\text{FOLLOW}(S)=\{\$\}$
2. 对于每条产生式，如果其右部含有非终结符，对于每一个非终结符$B$，将产生式视为$A\rightarrow \alpha B \beta$形式，首先令$\text{FOLLOW}(B)\leftarrow \text{FOLLOW}(B)\cup (\text{FIRST}(\beta)-\{\varepsilon\})$。如果$\beta\Rightarrow^* \varepsilon$或$\beta=\varepsilon$，还要$\text{FOLLOW}(B)\leftarrow \text{FOLLOW}(B)\cup \text{FOLLOW}(A)$
3. 重复第三步，直到所有非终结符的 FOLLOW 集不再变化

实际操作中，还有以下几点优化：

• 右部没有非终结符的产生式，可以直接划掉，不再考虑
• 如果产生式形如$A\rightarrow \alpha B$，直接$\text{FOLLOW}(B)\leftarrow \text{FOLLOW}(B)\cup \text{FOLLOW}(A)$即可，因为$\text{FIRST}(\varepsilon)-\{\varepsilon\}$为空集
• 若某个非终结符不出现在任何现存的产生式右部，则这个非终结符的 FOLLOW 集就不再变化，已经确定了，称这个终结符为“已求出的”
• 若产生式右部的非终结符都是“已求出的”，处理过一次之后也可以划掉

1.4、LL(1) 文法

LL(1)文法名称的含义：

• 第一个 L 表示从左到右扫描输入串
• 第二个 L 表示最左推导（总是选择最左边的非终结符进行推导）
• 1 表示只需要“向前看”一个符号即可以确定选用哪个产生式进行推导，也即之前说的“指针指向的符号”

一个上下文无关文法是 LL(1)文法的充分必要条件是：对于任意两个左部相同的产生式$A\rightarrow\alpha | \beta$，有：

• $\text{FIRST}(\alpha)\cap \text{FIRST}(\beta)=\emptyset$
• 如果$\varepsilon\in \text{FIRST}(\alpha)$，则$\text{FIRST}(\beta)\cap \text{FOLLOW}(A)=\emptyset$

这两个条件就对应着我们之前的表述：

• 如果左部（单个非终结符）相同的产生式的右部的 FIRST 集两两不相交，则推导过程是唯一确定的。
• 如果所有产生式的任一非空右部的 FIRST 集和其左部的 FOLLOW 集互不相交，则推导过程是唯一确定的。

LL(1)文法能够进行确定的自顶向下分析，具体的有递归下降预测分析以及基于预测分析表的 LL(1)分析两种方法。

1.5、递归下降预测分析

一个递归下降预测分析解析器的开发流程如下：

1. 消除二义性
2. 消除左递归
3. 提取左公因子
4. 从语法构造转换图
5. 简化转换图
6. 根据转换图手工编写解析器代码

我们会为每一个非终结符编写一个递归函数。递归下降预测分析不仅可以用于 LL(1)文法，也可以用于更一般的 LL(k)文法的文法。

---

对于每个非终结符$A$，产生式$A\rightarrow X_1X_2\dots X_n$，可以画出转化图，从一个初始状态到一个终态，边依次标记为$X_1, X_2, \dots, X_n$。

例如$E'\rightarrow +TE'|\varepsilon$，可以画出转化图如下：

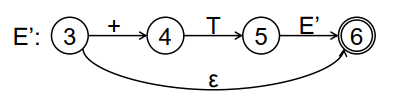
其可以经过化简，最终变成这样：

---

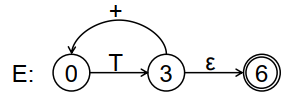
得到非终结符的转换图后，为每个图/非终结符编写一个递归过程：

• 如果路径中边的符号是终结符，则执行匹配（match）动作
• 如果路径中边的符号是非终结符，则执行派生（derive）动作，调用这个非终结符的递归过程

例如对于上面的转换图，可以编写如下的递归过程：

void E(){
  if(lookahead in FIRST(T)){
    T();
  } else error();
  while(lookhead=='+'){
    match('+');
    if(lookahead in FIRST(T)){
      T();
    } else error();
  }
  if(lookahead in FOLLOW(E)){
    return;
  } else error();
}

void match(Token tok)
{
  if(lookahead==tok){
    lookahead=nextToken();
  } else error();
}

在准备进入或者离开一个递归时，总是先检查 FIRST 集或者 FOLLOW 集，来看是否能拓展。

1.6、LL(1) 分析

对于 LL(1)文法，可以进行 LL(1)分析，其基本思想是建立一个预测分析表。解析时，通过查表来决定下一步的动作。

1.6.1、预测分析表

预测分析表是一个二维表格。每行代表非终结符，每列代表输入符号（包括结束符$\$$）。表格中的元素$M[A] [a]$的含义是，非终结符$A$面临输入符号$a$时，应该选取的产生式。如果为空，则转向错误处理。

---

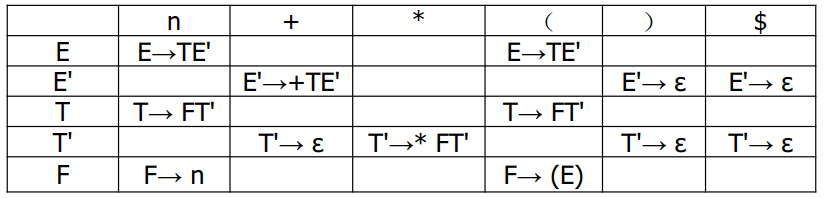
构造预测分析表的方法如下：对于文法的每个产生式$A\rightarrow\alpha$:

• 对于$\text{FIRST}(\alpha)$中的每个终结符$a$，将$A\rightarrow\alpha$这个产生式填入$M[A][a]$
• 如果$\varepsilon\in \text{FIRST}(\alpha)$，则对于$\text{FOLLOW}(A)$中的每个终结符$b$，将$A\rightarrow\alpha$这个产生式填入$M[A] [b]$。如果$\$\in \text{FOLLOW}(A)$，则将$A\rightarrow\alpha$这个产生式填入$M[A] [\$]$

LL(1)文法的定义保证了表格中至多只有一个产生式，所以后面做解析的时候，动作总是唯一的。如果出现了多个表达式，说明文法不是 LL(1)文法，可能存在左递归、左公因子、二义性等问题，应该先消除这些情况再建表。

1.6.2、Table-Drive Parser

构建好预测分析表后，就可以着手构建一个由预测分析表驱动的解析器程序了。解析器程序包括：

• 预测分析表
• 解析程序
• 栈：用于存储当前的匹配情况
• 输入缓冲区：存储输入串
• 输出流：输出结果或者报错信息

一开始，栈st中依次压入终止符$\$$和开始符号$S$，lookahead指针指向输入串s的开头。下面的伪代码描述了解析器的工作流程：

while(!st.empty() && st.top()!='$')
{
  auto X=st.top();
  st.pop();
  if(X in V_T)
  {
    if(X==lookahead)
    {
      // 如果栈顶符号和输入符号相同，弹出栈顶符号，指针后移
      st.pop();
      lookahead=nextToken();
    }
    else
      error();
  }
  else if(X in V_N)
  {
    if(M[X][lookahead]==X->alpha_1 alpha2 ... alpha_n)
    {
      // 如果栈顶符号是非终结符，且预测分析表中对应元素是某产生式。弹栈，将产生式右部逆序压栈
      st.pop();
      for(auto it=alpha.rbegin(); it!=alpha.rend(); it++)
        st.push(*it);
    }
    else
      error(); // 预测分析表中对应元素为空，报错
  }
}

if(lookahead=='$')
  accept();
else
  error();

1.6.3、恐慌模式

实际的编译器，通常能返回所有的错误。换句话说，在遇到错误时不会停止解析，而是继续解析，直到解析结束。

恐慌模式就是这样的一种错误恢复策略，当 parse 遇到一个无法处理的错误时，简单粗暴地忽略/跳过一些符号，继续处理。

---

在上面的伪代码中，有三种情况会报错：

• 输入符号和栈顶符号同是终结符，但是不匹配
• 预测分析表中对应元素为空
• 栈已空，但是输入符号还有剩余

---

我们在原来预测分析表的基础上，引入一种特殊的同步符号synch：产生式$A\rightarrow \alpha$，对于所有$a\in \text{FOLLOW}(A)$，将synch填入$M[A][a]$。

同时改变匹配的逻辑：

bool exist_error=false;
while(!st.empty())
{
  auto X=st.top();
  st.pop();
  if(X in V_T)
  {
    if(X==lookahead)
    {
      // 如果栈顶符号和输入符号相同，弹出栈顶符号，指针后移
      st.pop();
      lookahead=nextToken();
    }
    else
    {
      // 栈顶符号和输入符号不匹配，由于是非终结符，不可能直接匹配，直接跳过这个栈顶符号
      st.pop();
      exist_error=true;
    }
  }
  else if(X in V_N)
  {
    if(M[X][lookahead]==X->alpha_1 alpha_2 ... alpha_n)
    {
      st.pop();
      for(auto it=alpha.rbegin(); it!=alpha.rend(); it++)
        st.push(*it);
    }
    else
    {
      if(M[X][lookahead]==synch)
      {
        // 预测分析表中对应元素是 synch，说明输入符号当前匹配不了，但是有可能会在后面出现，直接跳过这个栈顶符号
        st.pop();
        exist_error=true;
      }
      else
      {
        // 当前输入符号不可能被匹配，直接跳过这个输入符号
        lookahead=nextToken();
        exist_error=true;
      }
    }
  }
}

if(exist_error)
  end();
else
  accept();

如上，在解析时，不会在遇到错误时立马停止，而是继续解析。同时最后判定是否接受，要看在解析过程中是否出现了错误。

2、自底向上分析

自底向上分析，是从输入符号串开始，逐步归约到开始符号。

最右推导是规范推导，相对应的，从左向右的规约称为规范规约。

自顶向上分析每一步的核心，是确定一个子串去规约，这个子串称之为可规约串。之前已经提到，规范规约可以取最左直接短语/句柄作为可规约串。

2.1、移进规约分析

移进规约分析（Shift-Reduce Parsing）是自底向上分析的一类方法，也是表驱动的分析方法：

---

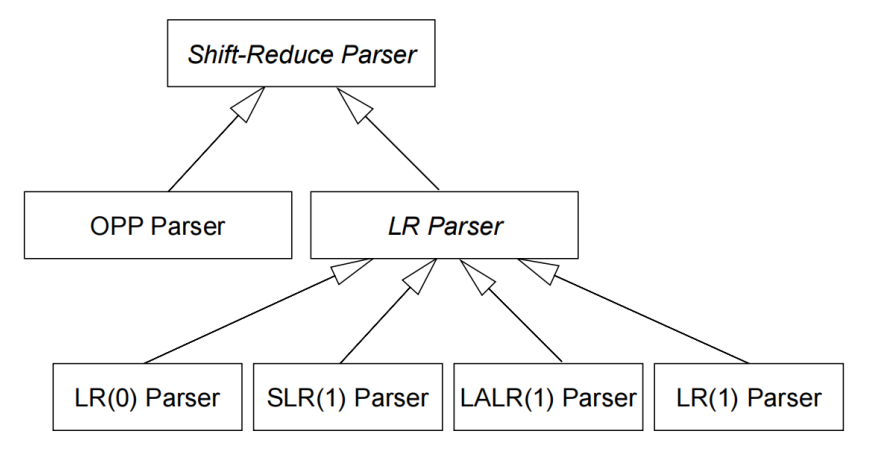
移进规约分析的基本思想是：

• 引入一个栈，一开始栈中只有一个结束符$\$$，指针指向输入串的开头
• 从左到右扫描输入串，把当前符号压入栈中，也即移进操作。边移进边分析，一旦栈顶符号串形成了某个句型的句柄（某个产生式的右部），就用相应的非终结符（该产生式的左部）来替换，也即规约操作。
• 重复上述过程，直到处理完整个输入串。如果此时栈中只剩下开始符号，则接受输入串；否则，拒绝输入串。

显然，如果只是这样，在规约过程中，可能会有犹豫，也即无法确定采用哪个产生式进行规约。例如$E+E*E$，到底是规约$E+E$还是$E*E$呢？

2.2、算符优先分析

算符优先分析（Operator-Precedence Parsing）是一种移进规约分析的方法。其基本思想是只定义好终结符之间的优先关系，然后根据这个优先关系来指导分析过程。算符优先分析不是规范规约，而且只适用于算符文法。

对于一个上下文无关文法，如果其任意一个产生式的右部都没有两个非终结符相连，而且该文法中不含空表达式，则这个文法就是算符文法。

---

仅考虑终结符之间的优先关系。优先关系存在于句型中“相邻”的两个终结符号。根据算符文法的定义，两个终结符不能真正相邻，这里的“相邻”指的是两个终结符之间没有其他的终结符，但是有非终结符。

“相邻”的两个算符$a, b$之间有三种有限关系：

• $a$的优先级高于$b$，记作$a\succ b$
• $a$的优先级等于$b$，记作$a\equiv b$
• $a$的优先级低于$b$，记作$a\prec b$

这里虽然使用了偏序的符号，但是优先关系不具备自反性、对称性和传递性。

根据优先关系，可以定义算符优先关系表，形如：

---

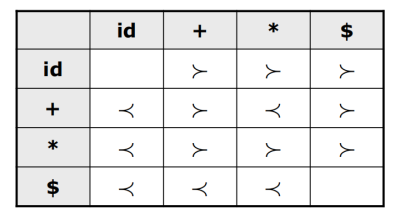
算符优先分析中，取最左素短语作为可规约串，无法规约单个的非终结符。

算符文法中，如果某个句型的短语至少包含一个终结符，而且除了这个短语本身之外不包含其他素短语，则这个短语就是素短语。最左边的素短语称为最左素短语。

---

算符优先分析的具体流程如下：

1. 初始，栈中只有结束符$\$$，指针指向输入串的开头

2. 考虑当前输入符号$a_{j+1}$

   • 如果是非终结符，直接移进
   • 如果是终结符，与栈顶符号$a_j$比较优先级（如果栈顶符号不是终结符，则再下一个符号一定是终结符）。
     • 如果$a_j\prec a_{j+1}$或$a_j\equiv b$，则移进
     • 如果$a_j\succ a_{j+1}$，则$a_j$就是某个最左素短语的尾。从栈的顶部开始，自顶向下寻找这个最左素短语的头，也即找到首对满足$a_{i-1}\prec a_i$的“相邻”的两个终结符。则$a_i....a_j$就是最左素短语，用对应的产生式$A\rightarrow N_i a_i N_{i+1} a_{i+1} \dots a_j N_{j+1}$进行规约。这里的$N_i, N_{i+1}, \dots, N_{j+1}$可以是空串或者任意的非终结符。

3. 重复上述过程，直到指针指向输入串的结束。如果此时栈中只剩下一个开始符号和一个非终结符，则接受输入串；否则，拒绝输入串。

可以注意到算符优先分析中，不在意非终结符之间的区别。在归约过程中，认为非终结符都是相同的，即便它们的名字可能不同，这一点不同于规范规约：

---

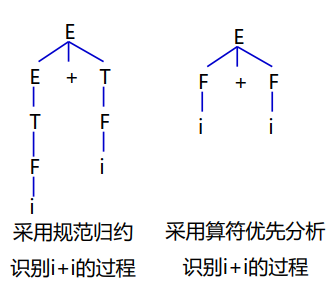
算符优先分析的缺点：

• 适用范围窄，只适合算符文法
• 会得到错误的规约。因为在规约过程中，不关注产生式右部非终结符的名字，只要对应位置上有非终结符就可以规约。

---

假设算符文法中有$n$个终结符，则算符优先关系表是一个$(n+1)\times(n+1)$（包括结束符）的矩阵，占用空间较大。

可以考虑构造优先函数$f, g: V_T \rightarrow Z$使得：

• 若$a\equiv b$，则$f(a)=g(b)$
• 若$a\succ b$，则$f(a)>g(b)$
• 若$a\prec b$，则$f(a)<g(b)$

则仅需要$2(n+1)$的空间，保存优先函数表即可。

这种方法的缺点是，一些原来可能没有优先关系的终结符之间，可能会被强制赋予优先关系，例如两个相同的终结符之间。

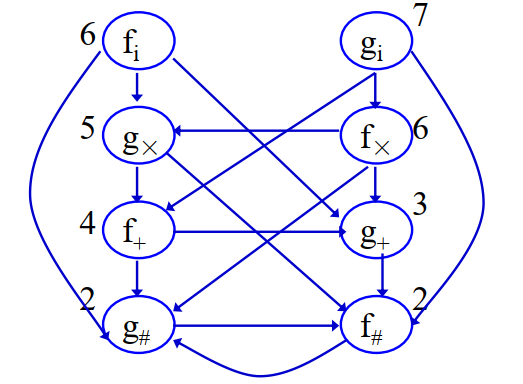
可以通过画一个图来方便地构造优先函数表。每一个终结符（包括结束符）$a$，有两个节点$f_a, g_a$。如果有$a\succ b$或$a\equiv b$，则由$f_a$到$g_b$画一条有向边；如果有$a\prec b$或$a\equiv b$，则由$g_a$到$f_b$画一条有向边。然后给各个节点赋值，保证本节点的值大于其直接连接的所有节点的值即可。

3、LR 分析

LR 分析是一类自底向上分析的方法。其基本思想是根据当前分析栈中的符号串（通常以状态表示），并向前顺序查看输入串的$k(k\geqslant 0)$个符号，来确定句柄，从而进行规约。

目前最流行的自底向上语法分析器都是基于 LR(k)语法分析，名字中：

• L 表示从左到右扫描输入串
• R 表示是最右推导的逆过程（也即最左规约）
• k 表示向前查看输入串符号的个数。LR(1)就能够满足当前绝大多数高级语言的需要了，当省略 k 时，一般也指的是 LR(1)。

LR 分析是规范规约，适用范围广，适用于大多数上下文无关文法描述的语言，且分析速度快。缺点则是 LR 分析器的构造工作量很大。

3.1、LR(0) 分析

LR(0)分析仅凭符号栈中的符号串即可确定句柄，做出规约决策，不需要向前查看输入串的符号。虽然 LR(0)对文法的限制很大，对绝大多数高级语言不适用，但是其是其他 LR 分析的基础。

3.1.1、项目

LR 语法分析器会维护一些状态，用这些状态来表明我们在语法分析过程中所处的位置，从而决定是规约还是移进。状态由项目集（Item Set）表示。

项目由在产生式的右部的适当位置插入一个圆点构成，例如$A\rightarrow X \cdot YZ$。每一个项可以理解为，当前状态下，对于这个产生式，我们分析到了哪个位置。圆点前面的就是以及分析过的部分，圆点后面的就是待分析的部分（或者说，如果想要用这个产生式规约，会希望看到的部分）。接下来具体来看：

• 圆点在最左边，例如$A\rightarrow \cdot XYZ$，尚未识别到任何部分，希望接下来能看到$XYZ$，这样就能规约了
• 圆点的左部，例如$A\rightarrow X \cdot YZ$，其中$X$表示分析过程中已经识别过的部分；圆点右部$YZ$则代表着接下来希望看到的部分
• 圆点在最右边，例如$A\rightarrow XYZ \cdot$，说明对于该产生式，其右部均已识别到了，已经形成了一个句柄，可以进行规约了

项目有不同的种类：

• 移进项目（Shift Item）：形如$A\rightarrow \alpha \cdot a \beta$的项目，其中$a\in V_T, \alpha, \beta\in V^*$，也即圆点后是终结符的项目。对于这种项目，选择把$a$移进符号栈。
• 待约项目（Reduce-expected Item）：形如$A\rightarrow \alpha \cdot B\beta$，其中$B\in V_N, \alpha, \beta\in V^*$，也即圆点后是非终结符的项目。对于这种项目，如果想要用这个产生式进行规约，则想要由某个左部为$B$的产生式规约出$B$，也即期望接下来分析时，能够首先规约得到$B$。
• 规约项目（Reduce Item）：形如$A\rightarrow \alpha \cdot$的项目，其中$\alpha\in V^*$，也即圆点在最右边的项目。对于这种项目，表示产生式的右部已经分析完了，句柄已经形成，可以把$\alpha$规约为$A$。
• 接受项目（Accept Item）：形如$S'\rightarrow S\cdot$的项目，其中$S'$是开始符号。对于这种项目，表示输入串可以规约为开始符号，分析结束。

3.1.2、LR(0) DFA

一个 LR(0)项目集，定义了 LR(0)自动机的一个状态。为了构造 LR(0)项目集，需要定义增广文法和两个函数——闭包函数 CLOSURE 以及跳转函数 GOTO。接下来依次介绍。

---

对于某个文法，新增开始符号$S'$以及产生式$S'\rightarrow S$，就得到了原文法的增广文法（Augmented Grammar，也称拓广文法）。需要定义增广文法的原因是：开始符号$S$可能出现在产生式的右部，规约过程中，不能判断是已经规约到了最初的开始符号，还是某个产生式右部的开始符号。引入$S'$后，由于$S'$只在产生式左部出现，所以不会混淆。

---

如果$I$是文法$G$的一个项目集，则得到$I$的闭包$\text{CLOSURE}(I)$的过程如下：

1. 一开始，令$\text{CLOSURE}(I)=I$
2. 若$A\rightarrow \alpha \cdot B \beta\in \text{CLOSURE}(I), B\in V_N$，则所有形如$B\rightarrow \cdot r$的项目也在$\text{CLOSURE}(I)$中
3. 重复第二步，直到没有新的项目加入$\text{CLOSURE}(I)$中为止

一个$\text{CLOSURE}(I)$就构成 DFA 中的一个状态。

---

设$I$为 DFA 中的一个状态，则其经过$X\in V_T \cup V_N$能够跳转到的状态$\text{GOTO}(I, X)$满足：

$$\text{GOTO}(I, X)=\text{CLOSURE}(J)=\text{CLOSURE}(\{A\rightarrow \alpha X \cdot \beta|A\rightarrow \alpha \cdot X \beta\in I, X\in V_T \cup V_N\})$$

其中$J$称之为核。这里之所以需要求闭包，是因为经过$X$，要首先规约得到$X$，所以要将与$X$相关的项目都加入进来。

实际上，就是将圆点右移，然后把相关的项目也加入进来。

---

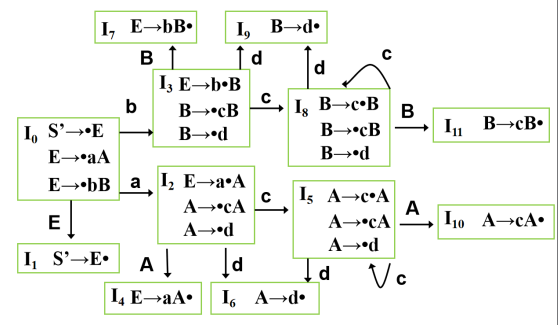
有了上面的铺垫，接下来可以构造 LR(0) DFA 了，DFA 中的每个状态都是一个项目集：

1. 构造初始状态$\text{IS}_0=\text{CLOSURE}(\{S'\rightarrow \cdot S\})$，且该状态是未被标记的。
2. 从 DFA 已有的部分，选择未被标记的某个状态$\text{IS}_i$。如果$\text{IS}_i$中含有项目$U\rightarrow x \cdot Ry$，其中$R\in V_T\cup V_N$，$x, y\in (V_T \cup V_N)^*$，则构造新状态$\text{IS}_j=\text{GOTO}(\text{IS}_i, R)$。然后将$\text{IS}_j$（未标记）加入到 DFA 中，且从$\text{IS}_i$到$\text{IS}_j$画一条有向边，标记为$R$。对所有这样的项目操作完后，标记$\text{IS}_i$。
3. 重复第二步，直到没有未标记的状态。

一个可能的 LR(0) DFA 如下图：

3.1.3、用 LR(0) DFA 进行分析

一个可行前缀（Viable Prefix）是一个规范句型的前缀，且该前缀没有越过句柄。

例如文法$G[S]$：

$$\begin{align*} &S\rightarrow aAcBe\\ &A\rightarrow b|Ab \\ &B\rightarrow d \end{align*}$$

则对于规范句型$aAbcde$，其句柄是$Ab$，则其可行前缀有$\varepsilon, a, aA, aAb$

一旦前缀包含了完整的句柄，就要进行规约了。所以可行前缀，也就是规约过程中，符号栈中可能出现的前缀。

---

如果存在一个推导过程$S\Rightarrow^* \alpha A \omega \Rightarrow \alpha \beta_1 \beta_2 \omega$，则称项目$A\rightarrow \beta_1 \cdot \beta_2$对于前缀$\alpha \beta_1$有效，或者说是$\alpha \beta_1$的有效项目。说人话就是，碰到$\alpha \beta_1$这个前缀，可以考虑$A\rightarrow \beta_1 \cdot \beta_2$这个项目。

进一步考虑$\beta_2$：

• 如果$\beta_2 \neq \varepsilon$，说明还没有形成完整的句柄，应该继续移进
• 如果$\beta_2 = \varepsilon$，说明已经形成了句柄，用产生式$A\rightarrow \beta_1$进行规约。

对于一个前缀，我们需要考虑所有的有效项目，这也是为什么 DFA 中的一个状态是项目集。之前介绍的 CLOSURE 以及 GOTO 就是为了得到关于一个前缀的所有有效项目：

• 考虑$A\rightarrow \beta_1 \cdot B \beta_2$，对于可行前缀$\alpha \beta_1$有效，则对这个项求闭包，新得到的项目$B\rightarrow \cdot \gamma$也是有效的。这是因为有$S'\Rightarrow^* \alpha A \omega \Rightarrow \alpha \beta_1 B \beta_2 \omega \Rightarrow \alpha \beta_1 \gamma \beta_2 \omega$，也即有$S'\Rightarrow^* \alpha \beta_1 B \beta_2 \omega \Rightarrow \alpha \beta_1 \gamma \beta_2 \omega$，由定义，所以$B\rightarrow \cdot \gamma$也是有效的。
• 考虑$A\rightarrow \beta_1 \cdot X \beta$，对于可行前缀$\alpha \beta_1$有效，则对这个项求 GOTO，首先$A\rightarrow \beta_1 X \cdot \beta_2$对$\alpha \beta_1 X$是有效的，因为$S'\Rightarrow^* \alpha A \omega \Rightarrow \alpha \beta_1 X \beta_2 \omega$，再套一个闭包，对$\alpha \beta_1 X$还是有效的。

所以利用之前的两个函数构造出的 LR(0) DFA，在 DFA 上移动，就相当于随着不断往符号栈中移进符号，然后考虑所有的有效项目。

3.1.4、构造 LR(0) 分析表

再次回顾一下 LR(0)分析的过程：从左往右扫描输入串，不断将符号移进符号串中，直到某个时刻，栈中出现了句柄，则进行规约。重复这个过程，直到输入串全部移进栈中，且归约到栈中只剩下开始符号$S'$。

则首先我们需要一个动作表 ACTION，表示当前状态下，面临输入符号（只可能是终结符，因为输入串全是非终结符）应该做的操作，是移进、规约、接受或者报错。

其次我们还需要一个转换表 GOTO，表示当前状态下，面临文法符号，应该转移到哪个状态。这对应了在 DFA 上的移动。

---

构造 ACTION 表的方法如下：

• 若项目$A\rightarrow \alpha \cdot a \beta, a\in V_T$在状态$IS_k$中，且$\text{GOTO}(k, a)=IS_j$，则令$\text{ACTION}[i][a]=S_j$。$S_j$即表示移进，然后转移到状态$j$。
• 若项目$A\rightarrow \alpha \cdot B \beta, B\in V_N$在状态$IS_k$中，且$\text{GOTO}(k, B)=IS_j$，则令$\text{GOTO}[i][B]=j$
• 若项目$A\rightarrow \alpha \cdot$在状态$IS_k$中，且产生式$A\rightarrow \alpha$的编号为$j$，则对于任何$a\in V_T \cup \{\$\}$，令$\text{ACTION}[k] [a]=R_j$。其中$R_j$表示用$j$号产生式进行规约。这里不用向前看任何符号，直接规约，再次说明这是 LR(0)分析。
• 若项目$S'\rightarrow S\cdot$在状态$IS_k$中，则令$\text{ACTION}[k][\$]=\text{ACC}$，表示接受。
• 其余空白的地方，表示错误

看起来复杂，其实就是根据之前得到的 DFA 图各个状态以及转移，来填充表格。如果边标记的是终结符，就是移进+转移，填充 ACTION 表；如果标记的是非终结符，就是转移，填充 GOTO 表；如果状态中有规约项目，就是规约，填充 ACTION 表的一整行。

由于 ACTION 表只有终结符部分，所以一般会将 GOTO 的终结符部分与 ACTION 表重叠。上面的 DFA 图对应的 LR(0)分析表如下：

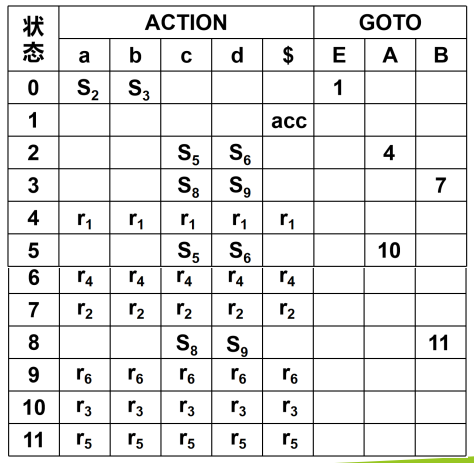
3.5、利用 LR(0) 分析表进行分析

LR(0)分析器的结构如下所示：

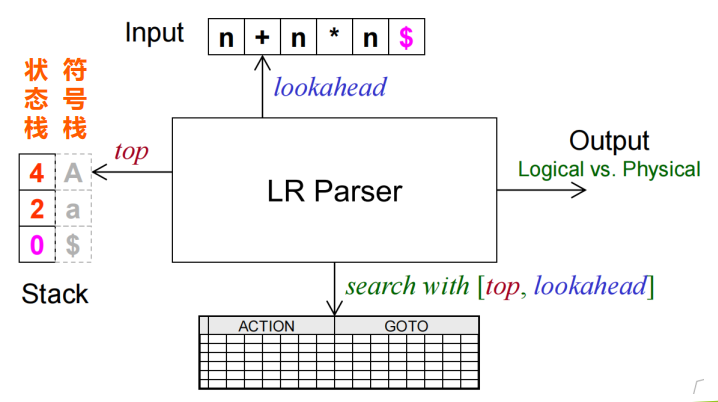
可见其还包括一个状态栈，其与符号栈是同进同出的。

利用 LR(0)分析表进行分析的过程如下：

1. 初始，状态栈中为初始状态 0，符号栈中只有结束符$\$$，输入串指针指向输入串的开头。

2. 状态栈栈顶为$i$，且当前输入符号$a$：

   • 若$a$是终结符，且$\text{ACTION}[i][a]=S_j$，则移进$a$，并将状态$j$压入状态栈中，指针后移
   • 若$a$是终结符或$\$$，且$\text{ACTION}[i] [a]=R_j$，则用$j$号产生式$A\rightarrow \beta$进行规约。符号栈与状态栈都弹栈$k=|\beta|$次，状态栈新栈顶为$i'$。然后将$A$压入符号栈中，将$\text{GOTO}[i'] [A]$压入状态栈中。
   • 若$\text{ACTION}[i][a]=\text{ACC}$，则接受输入串
   • 若$\text{ACTION}[i][a]=\text{ERROR}$，则报错

3.2、SLR(1) 分析

考虑构造出的 DFA 中的某个状态有以下状况：

• 移进-规约冲突：项目$A\rightarrow \alpha \cdot a \beta$和$B\rightarrow r\cdot$在同一个状态（项目集）中，则在该状态下遇到输入符号$a$，不能确定是移进$a$还是进行规约。
• 规约-规约冲突：项目$A\rightarrow \alpha \cdot$和$B\rightarrow r\cdot$在同一个状态（项目集）中，则在该状态下，不管面临什么输入符号，都不能确定如何规约。

如果一个文法的 LR(0) DFA 中，不存在移进-规约冲突和规约-规约冲突，则称这个文法是LR(0)文法。

---

遇到上面这种冲突时，我们需要额外的信息来帮助我们决策。

考虑下面这种方法：对于规约项目$A\rightarrow \alpha \cdot$，只有当下一个输入符号$a\in \text{FOLLOW}(A)$时，才可以进行规约。

这种基于 LR(0)分析，且只有在遇到冲突时才向前查看一个符号的分析方法，称为SLR(1)分析（Simple LR(1) 分析）。

如果一个文法中所有项目冲突，都能够通过上面的方法解决，则称这个文法是SLR(1)文法。

---

SLR(1)分析表的构造方法与 LR(0)分析表类似，唯一的区别在于对于项目集中规约项目的处理：若项目$A\rightarrow \alpha \cdot$在状态$IS_k$中，且产生式$A\rightarrow \alpha$的编号为$j$，则对于任何$a\in (V_T \cup \{\$\}) \cap \text{FOLLOW}(A)$，置$\text{ACTION}[k] [a]=R_j$。

注意到，这里不是填一整行的$R_j$，而是只填在$\text{FOLLOW}(A)$中的符号对应的列上。

---

容易发现，SLR(1)分析并不能完全解决这两种冲突：

• 对于移进-规约冲突：还是考虑项目$A\rightarrow \alpha \cdot a \beta$和$B\rightarrow r\cdot$在同一个状态中，如果$a\in \text{FOLLOW}(B)$，仍然无法确定是该移进还是该规约。
• 对于规约-规约冲突：还是考虑项目$A\rightarrow \alpha \cdot$和$B\rightarrow r\cdot$在同一个状态中，如果$\text{FOLLOW}(A)\cap \text{FOLLOW}(B) \neq \emptyset$，当下一个输入符号正好是交集中的某个符号时，仍然无法确定是规约为$A$还是规约为$B$。

SLR(1)虽然利用 FOLLOWb 集作为展望信息，解决了一部分冲突。但是 FOLLOW 集与 FOLLOW 集、FOLLOW 集与移进符号之间可能有交集。而且$\text{FOLLOW}(A)$中的每一个符号都会出现在含$A$的某个句型中，也就是说利用 FOLLOW 集作为展望信息有时会显得太“严格”了。

3.3、LR(1) 分析

LR(1)分析，顾名思义，也会向前看一个符号。相比 SLR(1)，LR(1)会为每一个句型都设置展望信息，而不仅仅是在遇到冲突时才使用。

LR(1)项目，在 LR(0)项目的基础上增加了一个向前搜索符号集（Lookahead Symbol，也称为展望符号），表示产生式右端完全匹配后，所允许的下一个输入符号的集合。

一个具体的 LR(1)项目形如$[A\rightarrow \alpha \cdot \beta, a|b]$。对于形如$[A\rightarrow \alpha \cdot, a]$的 LR(1)项目，只有当下一个输入符号是$a$或者$b$时，才可以进行规约。

---

LR(1)的初始项目集、CLOSURE、GOTO 函数相应也有变化。

LR(1)的初始项目集为$\text{IS}_0=\text{CLOSURE}(\{S'\rightarrow \cdot S, \$\})$，要想进行最后一步规约得到开始符号$S'$，必须已经到达了输入串的末尾，也即下一个输入符号是结束符$\$$。

LR(1)的 CLOSURE 函数定义变化为：

1. 一开始，令$\text{CLOSURE}(I)=I$
2. 若$[A\rightarrow \alpha \cdot B \beta, a]\in \text{CLOSURE}(I), B\in V_N$，则所有形如$[B\rightarrow \cdot r, b]$的项目也在$\text{CLOSURE}(I)$中，其中$b\in \text{FIRST}(\beta a)$
3. 重复第二步，直到没有新的项目加入$\text{CLOSURE}(I)$中为止

LR(1)的 GOTO 函数定义变化为：

$$\text{GOTO}(I, X)=\text{CLOSURE}(J)=\text{CLOSURE}(\{[A\rightarrow \alpha X \cdot \beta, a]|[A\rightarrow \alpha \cdot X \beta, a]\in I, X\in V_T \cup V_N\})$$

---

如果一个文法的 LR(1)项目集中没有移进-归约或归约-归约冲突，则称该文法为 LR(1)文法

显然根据定义，如果一个文法是 LR(0)文法，则其也一定是 SLR(1)文法和 LR(1)文法，反之则不然。

LR(1)文法的优点在于比较确切，可以消除更多的无效规约，适用的文法更多。其缺点在于，LR(1)分析也有局限性，不能消除所有的冲突，此时可以考虑 LR(k)分析。另一个缺点在于，LR(1)分析中的状态数目相比于 LR(0)会更大，还可能存在状态的冗余。这就引出了接下来要介绍的 LALR(1)分析。

3.4、LALR(1) 分析

一个 LR(1)项目集可以分为两部分，产生式的集合——心，以及向前搜索符的集合。

具有相同的心的 LR(1)项目集可以合并。例如下图展示$I_3, I_6$和$I_8, I_9$合并前后的情况：

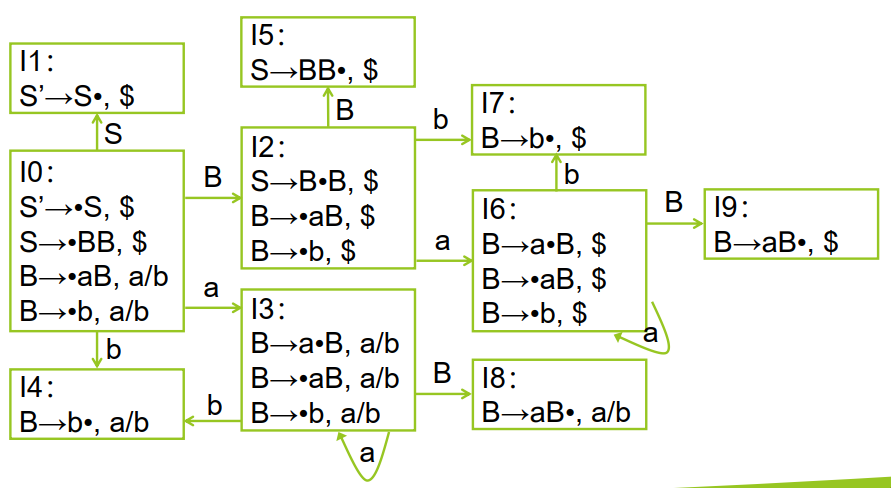
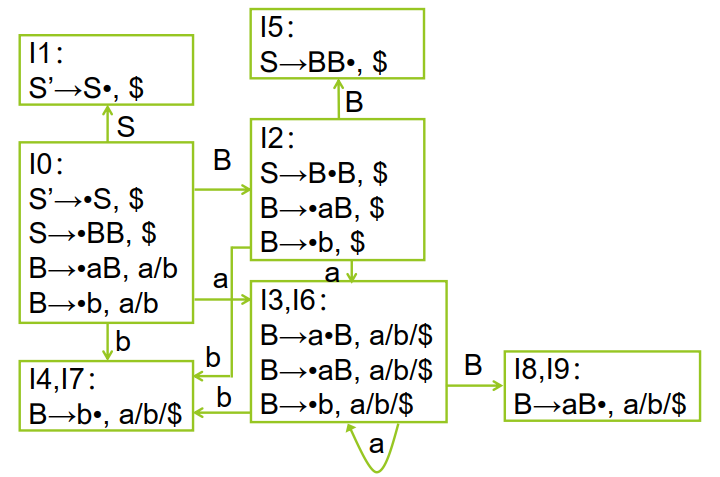
如果将所有的同心集合并之后，不包含规约——规约冲突（上一步的 LR(1) DFA 中已经不会包含移进-规约冲突，只可能出现新的归约——归约冲突），则可以使用 LALR(1) 分析。合并后的项目集就称为 LALR(1) 项目集，对应的文法就称为LALR(1)文法。

---

合并同心集之后，由于向前搜索符号集扩大，一些错误的发现可能会被推迟，但是错误的位置仍然是准确的。

LALR(1)是 LR(1)的优化版本，可以大大减少项目集的数目。它是一种介于 SLR(1)和 LR(1)之间的一种方法，其功能比 LR(0)和 SLR(1)强，但是比 LR(1)弱（向前搜索符号集扩大，相当于更宽松）。其适用范围相比 LR(1)也更广。

LALR(1)能够处理大多数编程语言的语法，Yacc 和 Bison 等工具默认使用 LALR(1)分析。

3.5、对比与总结

LR(0)分析无需向前查看任何输入字符，仅依赖当前状态就可规约。特点是分析表中可能存在一整行的$R_j$。

可能存在冲突，可以尝试使用 SLR(1)或其他分析方法解决。

---

SLR(1)分析基于 LR(0)分析，向前查看一个输入字符，只有这个输入字符$a\in \text{FOLLOW}(A)$时才进行规约。特点是分析表中只用$\text{FOLLOW}(A)$中字符所在的列才能填写$R_j$，相比 LR(0)更精确。

还可能存在无法解决的冲突，可以尝试使用 LR(1) 来解决。

---

LR(1) 分析也是基于 LR(0) 分析，给每个项目显式增加一个向前搜索符号集。特点是分析表中只有在向前搜索符号集中的字符所在的列才能填写$R_j$，相比 SLR(1)更精确。

LR(1) 分析可以解决绝大部分的冲突，如果仍然存在冲突，可以尝试使用可以考虑进一步的 LR(k)分析（$k\geqslant 2$）来解决。

---

LALR(1)分析基于 LR(1)分析，合并 LR(1)项目集中的同心集，如果合并后不存在冲突，则可以进行 LALR(1)分析。

综合来说，LALR(1) 比 LR(1) 弱，但是比 SLR(1)强，是精确性和效率的折中。

3.6、二义性文法的 LR 分析

对于二义性文法，可以选择先消除二义性，再进行 LR 分析。也可以直接进行 LR 分析，但是根据优先关系和结合性认为添加一些限制。

例如二义性文法$G$，只有一个产生式$E\rightarrow E+E|E*E|(E)|i$。

假如当前符号栈里为$\$ E+E$，对应状态集$\{E\rightarrow E+E\cdot, E\rightarrow E\cdot+E, E\rightarrow E\cdot*E\}$。如果规定了$*$的优先级高于$+$，且相同符号之间为左结合，就可以确定：

• 下一个符号为$*$，应该移进
• 下一个符号为$+$，应该用$E\rightarrow E+E$规约

3.7、LR 分析中的错误恢复

LR 分析的错误恢复同样可以采取恐慌模式。如果当前状态面临当前输入符号没有合法动作（分析表中对应位置空白），则会进行以下步骤：

1. 状态栈中自顶向下扫描，直到找到某一个状态$S$，其在 GOTO 表中有值，也即存在一个非终结符$A$使得$\text{GOTO}[S][A]$非空。
2. 忽略接下来的零个或者多个输入符号，直到某个输入符号$a$满足$a\in \text{FOLLOW}(A)$
3. 将$\text{GOTO}[S][A]$压入状态栈中，继续分析

---

LR 分析还可以采取短语级别的错误恢复。其基本思路是给每一种报错（分析表中的每一个空白处），都构造一个恰当的恢复动作，然后将错误处理的例程填入到分析表中。

例如对于文法$G[E]: E\rightarrow E+E|E*E|(E)|i$，下面是填入了错误恢复例程的 SLR(1)分析表：

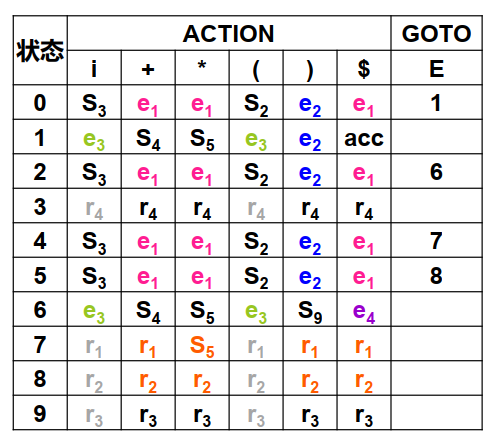
看其中的 0、2、4、5 状态，对于输入符号$+, *, \$$填入了错误恢复例程$e_1$。

这四个状态下，其实是希望读入$i$或者$($，也即希望读入一个二元算式的第一个运算数，但是却读到了一个运算符。

$e_1$做的就是，将状态 3 压入状态栈，符号$i$压入符号栈，然后报错“缺少运算数”。其实就是假装读入了运算数，让分析能够继续进行下去。

第五讲 语法制导翻译

1、概述

语法制导翻译（Syntax-Directed Translation），涵盖语义分析和中间代码生成两个部分。

语义分析过程，会收集各个标识符的属性信息，并检查输入程序是否符合语义规则。语义规则检查的方面包括：

• 数组下标越界
• 声明和使用的函数没有定义
• 零作除数
• 各种条件表达式的类型是否为布尔型
• 运算符的分量类型是否相容
• 赋值语句左右部的类型是否相容
• 形参和实参的类型是否相容
• x+f(...)中的f是不是函数名，形参和实参的数量/类型是否一致
• …

在进行语义检查的同时，如果扫描到声明部分，会构造标识符的符号表；扫描到语句部分时，会进行中间代码生成。

2、语法制导定义

语义制导定义（Syntax-Directed Definition，SDD）是上下文无关文法与属性和规则的结合，也称为属性文法（Attribute Grammar）：

• 属性：在普通文法的基础上，对文法中的每一个符号，引进一些属性来代表与文法符号相关的信息，例如类型、值、存储位置等。例如符号$X$有属性$a$就可以用$X.a$来表示。
• 规则：也即为每一个产生式配备的计算属性的规则，称为语义规则。其描述的工作也已包括属性计算、静态语义检查、符号表的操作、代码生成等等，有时候写成函数或者过程段。

---

属性可以分为两类：

• 综合属性（Synthesized Attribute）：从语法树的角度来看，如果一个节点的某个属性值，是由该节点的子节点的属性值计算得到的，则称这个属性为综合属性。也即从下往上计算。
• 继承属性（Inherited Attribute）：从语法树的角度来看，如果一个节点的某个属性值，是由该节点的父节点或者兄弟节点的属性值计算得到的，则称这个属性为继承属性。也即从上往下计算。

例如某个属性文法的产生式可能如下：

$$E\rightarrow E_1+T\ \{E.val=E_1.val+T.val\}$$

这里$E.val$就是一个继承属性。

一个只包含综合属性的 SDD 称为 S-属性的 SDD 或 S-属性文法。

显然终结符只可能有综合属性，由词法分析器直接提供。非终结符既可以有综合属性，也可以有继承属性，由语义规则计算得到。开始符号没有继承属性。

---

给语法树的每个节点标注上属性值，就得到了注释语法分析树（Annotated Parse Tree）：

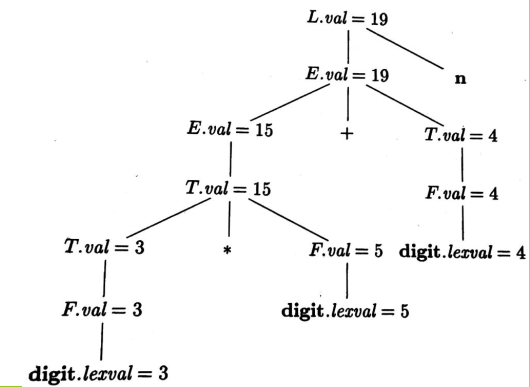
对一棵语法分析树的某个节点的一个属性进行求值之前，必须首先求出这个属性值所依赖的所有属性值。

对于 S-属性文法，可以按照自底向上的顺序计算出所有节点的属性值。

对于非 S-属性文法（同时有继承属性和综合属性），属性的计算不能完全按照自底向上的顺序，需要确定一个求值顺序——依赖图。

3、SSD 的求值顺序

依赖图（Dependency Graph）是一个有向图，刻画了对一颗语法分析树中不同节点的属性求值时，可能采取的顺序。如果依赖图中有一条$M\rightarrow N$的边，则要先对$M$对应的属性求值，才能对$N$对应的属性求值。

显然，利用拓扑排序，可以求出可能的求值顺序。对于有向无环图，一定存在一种可行的求值顺序能够求出所有节点的属性值。

---

抽象语法树（Abstract Syntax Tree，AST）相比语法分析树更简洁，直接反映了源代码的语法结构，剔除了无关的语法细节（例如分号、括号等）。

S-属性文法中，每个属性都是综合属性，每个节点的属性值仅由其子节点的属性值计算得到，是自底向上传递信息的，可以保证求值顺序与 LR 分析的输出顺序相同。在语法分析树上，可以用后序遍历的方式来完成。

---

如果一个 SDD 的产生式右部符号的属性之间，依赖关系总是从左到右的（Left to Right），则称这个 SDD 为L-属性的 SDD或L-属性文法。S-属性文法一定是 L-属性文法。

具体来说，L-属性文法中，每个属性：

• 要么是一个综合属性
• 要么是一个继承属性，且若产生式形如$A\rightarrow X_1X_2\cdots X_n$，其中$X_i$的继承属性$X_i.a$的只能依赖于：
  • $A$的继承属性
  • $X_1$、$X_2$、$\cdots$、$X_{i-1}$的综合属性或者继承属性（也即已经计算出来的或者可以在$X_i$之前计算出来的）
  • $X_i$本身的属性，且由$X_i$属性 组成的依赖图不存在环

总而言之，L-属性文法的定义使得其属性计算时可以按从左到右的顺序进行。

4、S-属性文法翻译方案

S-属性文法的翻译完全适用自底向上的翻译方法，只需再加上一个语义栈，与符号栈和状态栈同进同出，规约时，按照语义规则进行操作（求语义值/修改语义栈/弹栈等）即可。

5、L-属性文法翻译方案

L-属性文法适用于递归下降、LL(1)等自顶向下分析方法，采用深度优先访问语法分析树，其伪代码如下：

void dfvisit(n: Node){
  for(each child m of n, from left to right){
    cal inherited attr of m;
    dfvisit(m);
  }
  cal synthesized attr of n;
}

5.1、语法制导翻译方案

将属性文法的语义动作，具体的插入到产生式中，就得到了语法制导翻译方案（Syntax-Directed Translation Schemes，SDT）。利用翻译方案，就可以按照一定的规则，在语法分析的过程中进行语义动作的计算。

最常见的 SDT 是后缀 SDT，也即所有语义动作都在产生式的最右端：

一般的 SDT 中，语义动作可以放置在产生式右部的任何位置上。例如产生式$B\rightarrow X\{a\}Y$：

• 如果$X$是终结符，则识别到$X$之后，就会执行$a$
• 如果$X$是非终结符，则在识别到所有从$X$推导出的终结符（例如有$X\Rightarrow^* abcd$，就是识别到$abcd$）之后，才会执行$a$

如果语法分析是自底向上的，当$X$出现在栈顶时，动作$a$会执行；如果语法分析是自顶向下的，则在推导展开$Y$或者在输入中检测到$Y$之前，动作$a$会执行。

---

将一个 L-属性文法转化为 SDT 的规则：

• 计算每个非终结符$A$的继承属性的动作，插入到产生式中$A$之前的位置。如果有多个继承属性相互依赖（没有循环依赖），就需要按照拓扑排序来确定动作顺序。
• 计算产生式左部的综合属性的动作，插入到产生式的最右边

例如对于产生式$B\rightarrow B_1B_2$，有语义动作：

$$B_1.ps=B.ps\\ B_2.ps=B.ps\\ B.ht=\max(B_1.ht,B_2.ht)\\ B.dp=\max(B_1.dp,B_2.dp)\\$$

则写为翻译方案应该是：

$$B\rightarrow \{B.ps=B_1.ps\}B_1\\ \{B.ps=B_2.ps\}B_2\\ \{B.ht=\max(B_1.ht,B_2.ht); B.dp=\max(B_1.dp,B_2.dp); \}$$

5.2、递归下降预测翻译器

编写一个递归下降预测翻译器的步骤如下：

1. 根据文法，编写一个 LL(1)文法
2. 编写语义动作，变为 L-属性文法
3. 将 L-属性文法变为翻译方案
4. 消除翻译方案中的左递归（带有左递归的文法无法进行确定的自顶向下语法分析）
5. 编写翻译器

---

之前已经介绍过如何消除文法中的左递归，也即将$A\rightarrow A\alpha | \beta$改为$A\rightarrow \beta A'$, $A'\rightarrow \alpha A' | \varepsilon$。

翻译方案中的左递归，由于设计语义动作和属性的计算，方法略有不同：

• 语义动作中只涉及输出，不涉及计算。则可以将动作视为一个终结符，然后用上面的通用方法消除。

• 语义动作涉及计算，且 SDD 是 S-属性的。仍然用上面的方法消除左递归，但是需要调整语义动作。例如：

  $$\begin{aligned} &A\rightarrow A_1Y\{A.a=g(A_1.a, Y.y)\}\\ &A\rightarrow X\{A.a=f(X.x)\} \end{aligned}$$

  其中$A_1$就是$A$，这里是为了避免语义动作中有两个$A$会混淆改名了，所以上面存在左递归，且其中$A.a, X.x, Y.y$都是综合属性。

  可以将其变为：

  $$\begin{aligned} &A\rightarrow X\{R.i=f(X.x)\}R\{A.a=R.s\}\\ &R\rightarrow Y\{R_1.i=g(R.i, Y.y)\}R_1\{R.s=R_1.s\}\\ &R\rightarrow \varepsilon\{R.s=R.i\} \end{aligned}$$

---

递归下降预测翻译器的实际代码编写和之前提到的解析器类似，只是需要带上语义动作。

例如对于下面这面这段 SDD：

$$\begin{aligned} & \text{R}\rightarrow \text{addop}\ \text{T} \ \{\text{R}.i = \text{mknode}(\text{addop.lexeme}, \text{R}.i, \text{T}.nptr)\}\ \text{R}_1\ \{\text{R}.s=\text{R}_1.s\} \\ & \text{R} \rightarrow \varepsilon\ \{\text{R}.s=\text{R}.i\} \\ \end{aligned}$$

写出来的翻译器伪代码应该是：

SyntaxTreeNode R(SyntaxTreeNode i){
  SyntaxTreeNode s;
  SyntaxTreeNode t_nptr, r1_i, r1_s;
  char addopLexeme;

  if(lookahead==addop){
    addopLexeme=lookahead.lexeme;
    match(addop);
    t_nptr=T();
    r1_i=R1(i);
    r1_i=mknode(addopLexeme, i, t_nptr);
    s=r1_s;
  } else {
    s=i;
  }
  return s;
}

每个非终结符的函数，其参数代表该非终结符的继承属性（继承父节点的属性作为参数来计算本节点的属性），其返回值代表该非终结符的综合属性（本节点的属性返回给其他节点使用）。

在函数体中，要进行语法分析并执行语义动作，计算属性：

• 决定使用哪一个产生式来进行规约
• 需要检查下一个输入符号，如果符合，则调用match()，否则报错
• 声明局部变量保存必要的属性值，用于计算产生式右部非终结符的继承属性或者产生式左部的综合属性- 可能还需要调用产生式右部非终结符的函数，并提供相应的参数

5.3、在 LR 分析中实现 L-属性文法翻译

L-属性文法中，并不是所有语义动作都位于产生式体最右边，还有可能存在继承属性，所以在 LR 分析中，需要额外的措施来实现其翻译。

---

如果该 L-属性文法仅包含综合属性，只是有语义动作不在产生式体最右边，可以通过引入 marker 标记，将嵌入到中间的动作移到最右边，然后就可以按照正常 S-属性文法的翻译方案进行翻译。

例如对于下面这个 L-属性文法：

$$\begin{aligned} & E\rightarrow T R\\ & R\rightarrow +\ T\ \{ \text{print('+'')}\} \ R\ | -\ T\ \{\text{print('-')}\}\ R\ |\ \varepsilon \\ & T\rightarrow \text{num}\ \{ \text{print(num.val)} \} \end{aligned}$$

可以修改为：

$$\begin{aligned} & E\rightarrow T R\\ & R\rightarrow +\ T\ M\ R\ | -\ T\ N\ R\ |\ \varepsilon \\ & T\rightarrow \text{num}\ \{ \text{print(num.val)} \}\\ & M\rightarrow \varepsilon\ \{ \text{print('+')}\}\\ & N\rightarrow \varepsilon\ \{ \text{print('-')}\} \end{aligned}$$

---

如果该 L-属性文法还含有继承属性，可以分情况考虑：

• 最简单的情况，继承属性值是复制之前某个综合属性的值。例如$A\rightarrow XYZ\ \{Y.i=X.s\}$，则要准备将$XYZ$规约为$A$时，$X.s$已经存在于语义栈中了，直接使用即可。

• 稍复杂的情况，继承属性不是简单的复制。例如$S\rightarrow aA\ \{C.i=f(A.s)\}\ C$，当要计算$C.i$的时候，$A.s$已经在语义栈上了，但是$f(A.s)$不在。

  这个时候，也可以通过引入 marker 来解决。可以将上面的规则改写为：

  $$\begin{aligned} & S\rightarrow aA\ \{M.i=A.s\}\ M \ \{C.i=M.s\}\ C \\ & M\rightarrow \varepsilon\ \{M.s=f(M.i)\} \end{aligned}$$

  这样会先规约$M$，计算出$f(M.i)$，也即$f(A.s)$的值，放到语义栈中，之后规约$C$的时候，就可以直接用了。

• 更复杂的情况，对语义栈中之前属性的访问不确定。例如$S\rightarrow aA\ \{C.i=A.s\}\ C\ |\ bAB\ \{C.i=A.s\}\ C$

  这里计算$C.i$的时候要用$A.s$，但是不知道是要用stack[top-1]的，还是要用stack[top-2]的。如果不想使代码逻辑变复杂，可以引入 marker 来解决，改写为：

  $$S\rightarrow aA\ \{C.i=A.s\}\ C\ |\ bAB\ \{M.i=A.s\}\ M\ C\ \{C.i=M.s\}\ C$$

  这样统一访问stack[top-1]即可。

第六讲 中间代码生成

从这一步开始，做真正的翻译工作。中间代码生成进行初步翻译，生成等价于源程序的中间表示。

1、中间表示

中间表示（Intermediate Representation，IR）包括：

• 高级中间表示：AST、DAG 等，适用于静态类型检查等任务
• 低级中间表示：三地址码（Three Address Code，TAC）等，适用于依赖于具体机器的任务（如寄存器分配和指令选择等）

IR 的选择和设计都是针对于具体的应用和任务的。LLVM IR 是一个通用的 IR，TensorFlow XLA IR 事专门针对机器学习的计算图优化的 IR。C 语言有时也可以用作 IR。

1.1、AST 和 DAG

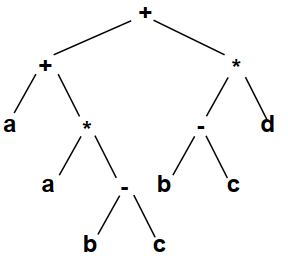
对于算数表达式a+a*(b-c)+(b-c)*d，可以用 AST 表示为：

用 DAG 则表示为：

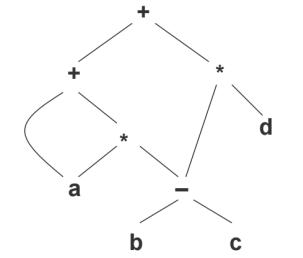
可以发现 DAG 中，复用了一些节点，构成了一个图（图中省略的箭头，所以虽然看起来是有环的，实际上没有）。

计算机中，采用值编码来构造 DAG。语法树/DAG 的节点存放在一个记录数组中，数组的每一行就是一个记录/节点。每个记录/节点都有一个编号，对于叶子节点，有一个附加字段，存放标识符的词法值；对于内部节点，有两个附加字段，指明两个子节点。

例如：

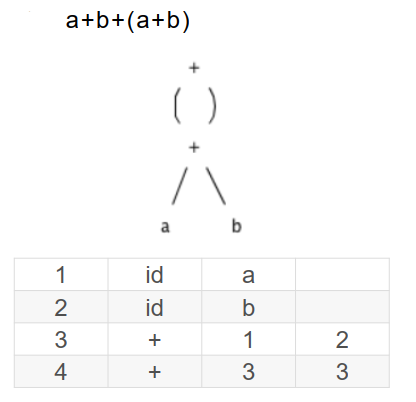
表中记录出现的顺序就是运算的顺序。

1.2、三地址码

三地址码中，一条指令的右侧最多有一个运算符，不允许出现组合的算术表达式。

对于算数表达式a+a*(b-c)+(b-c)*d，写成三地址码是：

t1=b-c
t2=a*t1
t3=a+t2
t4=t1*d
t5=t3+t4

三地址码的两个基本概念是地址和指令。

地址包括源代码中的变量名（会被替换为指向对应的符号表条目的指针）、常量以及编译器生成的临时变量。

指令是一个三元组，包括：

• x=y op z：二元运算
• x=op y：一元运算
• x=y：赋值
• goto L：无条件跳转，L代表要跳转到的行数
• if x goto L：有条件跳转
• if flase x goto L
• if x op y goto L：关系跳转
• param x1：参数传递
• call p,n：函数调用，p是函数名，n是参数数量
• return y：返回值
• x=y[i]：带下标的赋值指令，i代表偏移量（以字节为单位），而不是元素偏移量
• x=&y：取地址
• x=*y：解指针
• *x=y

函数调用时，先用若干条param指令传递参数，然后用一条call指令调用函数。

涉及跳转时，需要某个符号来标记要跳转的位置，据此三地址码可以分为带符号标号的三地址码：

L: t1=i+1
...
if t3<v goto L

以及带位置号/行号的三地址码：

100: t1=i+1
...
104: if t2<v goto 100

---

三地址码在计算机中具体的形式有三元式、间接三元式或者四元式等。

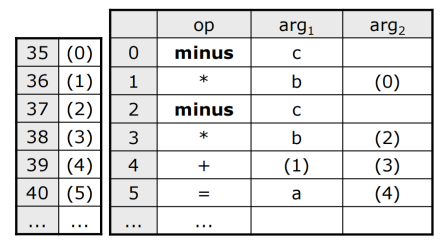
三元式（Triple）op, arg1, arg2，表示arg1 op arg2，结果用记录的序号来表示。带括号的数字表示指向相应三元式记录的指针。

例如

这种方法对运算结果的引用是依赖于记录位置的，如果某一条指令的位置变化，则所有相关的指令都要跟着改变。这不方便后续的优化。

间接三元式（Indirect Triple），与三元式类似，多了一个三元式指针列表。重排时，只需重排这个指针列表即可。

四元式（Quadruple）op, arg1, arg2, result，多一个字段专门用于放结果，所以改变指令顺序时无需担心。

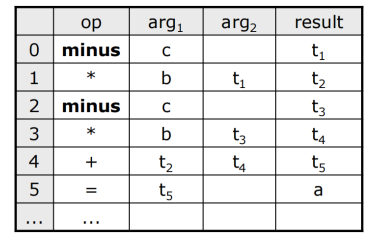
特别注意，一元表达式或者传参可能用不上arg2，跳转指令的目标放在result字段。

2、类型和声明

类型（Type）和声明（Declaration）

类型表达式包括：

• 基本类型。例如boolean、int、float、char等
• 类名
• 带类型构造算子array的式子。例如array(3, integer)等
• 带类型构造算子record的式子。例如record(a:integer, b:real)等
• 带类型构造算子$\rightarrow$的式子。例如$s\rightarrow t$表示从类型$s$到类型$t$的函数
• 笛卡尔积$\times$式。具有左结合性，优先级高于$\rightarrow$
• 取值为类型表达式的变量

通常，需要保证运算分量的类型和预算符的预期类型相匹配，根据强类型语言和弱类型语言，有不同程度的要求。

---

一个关于声明的文法例子如下：

$$\begin{aligned} &D\rightarrow T\ id\ ;\ D\ |\ \varepsilon\\ &T\rightarrow B\ id\ C\ |\ record\ \{\ D\ \} \\ &B\rightarrow int\ |\ double\\ &C\rightarrow [\ num\ ]\ C\ |\ \varepsilon \end{aligned}$$

类型的宽度（Width）是指类型所占用的存储单元的字节数。在声明文法中，还需要语义动作，计算出类型属性和宽度属性。

同时还需要计算出变量的地址，并加入符号表。体现在翻译方案中，如下所示：

$$\begin{aligned} &P\rightarrow \{\text{offset=0}\}\ D \\ &D\rightarrow T\ id\ ;\{\text{top.put(id.iexname, T.type, offset); offset+=T.width}\}\ D_1 \\ &D\rightarrow \varepsilon \\ \end{aligned}$$

特别地，记录类型（类似于 C 语言中的结构体）声明中的名字不能重复，这涉及到符号表的切换，且偏移也是相对记录内部而言的。所以对于记录而言，其翻译方案如下：

$$\begin{aligned} T\rightarrow & record\ \{\ \{\text{env.push(top); stack.push(offset); top=new Env(); offset=0; }\}\\ & D\ \}\ \{\text{T.type=record(top); T.width=offset; top=env.pop(); offset=stack.pop(); }\}\\ \end{aligned}$$

进入记录内部时，将原先的符号表和偏移量压栈暂时保存，创建一个新的符号表用于记录内部的变量声明，结束后恢复原先的符号表和偏移量。

3、表达式

表达式（Expression）

中间代码生成会涉及代码拼接（Code Concatenation）和增量生成（Incremental Generation）等手段。

---

用gen(...)表示生成括号内的代码的三地址码。，用||表示代码的拼接。

一个关于表达式的翻译方案如下图所示：

一个关于数组引用的翻译方案如下图所示：

其中L.addr是一个临时变量，用于计算数组的偏移量；L.array指向数组名对应的符号表的指针，L.type则是L生成的子数组的类型。

4、类型检查

对于强类型语言（例如 Python 和 Java），其类型规则严格，不允许（除语言明确允许之外的）隐式类型转换。类型错误会在编译时或者运行时被捕获，避免了潜在的错误。变量或者表达式的类型在编译时通常是确定的，且操作必须符合类型约束。

而弱类型语言（例如 C 和 JavaScript），其类型规则宽松，允许隐式类型转换。编译器或解释器可能会自动尝试转换类型以完成操作，可能导致意外行为。

例如，有关类型检查和转换的翻译方案的一部分可能如下图所示：

5、布尔表达式

布尔表达式（Boolean Expression）是一个特殊的表达式，它通常不仅涉及逻辑值的计算，还涉及控制流的跳转。所以我们接下来单独讨论布尔表达式的中间代码生成。

5.1、直接计算与短路计算

布尔表达式的产生式如下所示：

$$E\rightarrow E\ \text{or}\ E\ |\ E\ \text{and}\ E\ |\ \text{not}\ E\ |\ (E)\ |\ id\ rop\ id\ | \ \text{true}\ |\ \text{false}\$$

布尔运算符的优先顺序从高到底是$\text{not}$、$\text{and}$、$\text{or}$，且后两者是左结合，$\text{not}$是右结合。

$rop$代表关系运算符（各种比较运算符），$id$代表算数量。关系运算符的优先级都相同，高于任何布尔运算符，低于任何算术运算符。

我们知道，布尔表达式有短路运算的特性。在生成代码时，也要注意这一点。

---

直接计算（不考虑短路运算）时，布尔表达式的翻译方案如下所示：

特别注意到第五条涉及关系表达式时，一下生成了四条指令。例如a<b，生成的四元式是：

1: j<, a, b, (4)
2: =, 0, -, t1
3: jump, -, -,
4: =, 1, -, t1
5: ...

其中j<表示这是一个比较跳转指令，第一行等价于三地址码的if a < b goto (4)，要跳转到的指令放在result字段中。

---

对于布尔表达式的短路运算，我们需要给布尔表达式引入两个新的属性：

• B.true：布尔表达式的真出口，也即为真的时候，跳转到的指令
• B.false：布尔表达式的假出口，也即为假的时候，跳转到的指令

对于$S\rightarrow \text{if}\ (B)\ S_1\ \text{else}\ S_2$，我们生成的代码应该如下图所示：

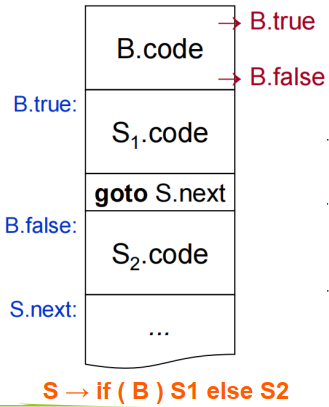
例如a<b || c<d && e>f，可以将其翻译为：

1: j<, a, b, B.true
2. jump, -, -, (3)
3: j<, c, d, (5)
4: jump, -, -, B.false
5: j>, e, f, B.true
6: jump, -, -, B.false

没有使用短路计算之前，这个布尔表达式需要 14 条四元式，且$\text{and}, \text{or}$指令会显式的生成。而使用短路计算之后，只需要 6 条四元式，且没有$\text{and}, \text{or}$指令了。

5.2、拉链与回填

在上面的短路计算中，B.true和B.false是尚未确定，要等后续代码生成完之后，才能确定真正的跳转位置。因此，我们要记录哪些指令需要回填（Backpatch）上B.true和B.false的值。

这些指令可以用额外的空间来存储，也可以用拉链技术，也即利用这些指令的result字段，来存储上一条需要回填的指令的地址，这样就可以形成一个链表。回填时，根据result字段，依次回溯到链表的头部，进行回填即可。

记merge(p1, p2)表示将两个子链合并：

• p2为空链时，直接返回p1
• p2不是空链时，将p2尾部的result字段指向p1的头部，然后返回p2的头部即可

记backpatch(p, i)表示将链表p中的所有指令的result字段都回填为i，也即将链表中的所有指令的跳转位置都改为i。

---

则具体的翻译方案如下图所示：

其中E.true和E.false分别表示布尔表达式的真出口和假出口，E.codebegin表示布尔表达式的代码开始位置，也即将要执行的指令地址。

对于其中第一条产生式的翻译方案，我们逐行解释：

1. E.codebegin=E1.codebegin：执行E，第一条指令就是E1的第一条指令
2. backpatch(E1.false, E2.codebegin)：或表达式，如果E1为假，接下来要执行的是E2，所以要将E1的假出口回填为E2的第一条指令
3. E.true=merge(E1.true, E2.true)：或表达式，如果E1为真，接下来要执行的是E2的真出口，所以要将E1的真出口和E2的真出口合并

第八讲 目标代码生成

目标代码生成是编译器的最后一个阶段，负责将中间代码转换为目标代码（通常汇编代码或者机器码），使得程序可以在特定的计算机上运行。这一部分任务包括寄存器分配、汇编指令选取以及进一步的机器相关优化等。

1、简介

目标代码生成，顾名思义，其主要任务就是代码生成，也即以中间代码作为输入，输出特定机器的汇编代码或者机器码。完成这个转换过程的程序称为代码生成器（Code Generator）。

代码生成要考虑的基本问题：

• 如何生成短的目标代码（占用空间小）
• 如何充分利用寄存器，减少访存次数（程序性能高）

无论是生成哪种机器的目标代码，代码生成都会涉及到寄存器分配算法、基本块代码生成算法等。

代码生成器主要会关注指令选择、寄存器的分配与指派、指令调度等问题。

---

指令选择（Instruction Selection）是选择合适的目标机器指令来实现 IR 语句，要在生成的代码的性能和代码大小之间权衡。

例如，对于a=a+1，可以生成：

LD R0, a
ADD R0, R0, #1
ST R0, a

或者：

INC a

前者更通用，但是更长，而且访问内存开销大；后者很简洁，但是某些架构可能不支持INC指令。

再比如将寄存器R0设为 0，可以生成：

LD R0, #0

或者：

XOR R0, R0, R0

前者简单直接，后者变为二进制更小。

因此，指令选择需要利用硬件特性，根据目标机器的指令集来选择最优的指令。

---

寄存器分配与指派（Register Allocation and Assignment）是为了高效利用寄存器资源，减少内存访问次数，其主要包括：

• 寄存器分配：选择在程序的每个点上，将哪些变量驻留在寄存器中
• 寄存器指派：为变量分配具体的寄存器

这部分要考虑到，寄存器数量有限，该怎么实现较优的分配，而且不同架构的寄存器数量和类型也不同。

---

指令调度（Instruction Scheduling）是决定指令执行顺序的过程。

这一步对现代流水线处理器至关重要，其核心目标时通过重新排列指令顺序，最大化利用 CPU 流水线，减少因为依赖关系导致的流水线停顿，提升指令级并行性（ILP）。

主要手段是将没有依赖关系的指令聚合在一起，同时保持语义不变。

2、目标机器的抽象

目标机器的抽象是指对目标机器的指令集、寻址方式、寄存器、内存模型等进行抽象，以便于编译器生成代码。

---

RISC（Reduced Instruction Set Computer，精简指令集计算机）架构支持以下指令：

LD dst, addr // 从内存addr处加载数据到寄存器dst
ST x, Ri // 将寄存器Ri的值存储到内存地址x
OP dst, src1, src2 // 对src1和src2进行二元运算，结果存储到dst
OP dst, src // 对src进行一元运算，结果存储到dst
BR L // 无条件跳转到标签L
Bcond r, L // 条件跳转，如果寄存器r满足条件，则跳转到标签L
...

寻址方式包括：

• #C：立即数寻址，表示取常量，开销为 1
• x：绝对寻址，表示取contents(x)，开销为 1
• *x：间接寻址，表示取contents(contents(x))，开销为 1
• R：直接寄存器寻址，表示取contents(R)，开销为 0
• *R：间接寄存器寻址，表示取contents(contents(R))，开销为 0
• a(Ri)：直接变址寻址，表示取contents(a+contents(Ri))，开销为 1
• *a(Ri)：间接变址寻址，表示取contents(contents(a+contents(Ri)))，开销为 1

其中contents(x)表示寄存器x或者内存地址x中的内容（也指代这个内容的地址）。

举几个实际例子：

• a[j]=c可以翻译为：

  LD R1, c
  LD R2, j
  MUL R2, R2, #4 // 假设每个元素占 4 字节
  ST a(R2), R1

• x=*p可以翻译为：

  LD R1, p
  LD R2, 0(R1)
  ST x, R2

• *p=y可以翻译为：

  LD R1, p
  LD R2, y
  ST 0(R1), R2

一条指令的代价=1+操作数寻址的代价，一个程序的代价=所有指令的代价之和。

3、目标代码中的地址

目标代码中，一个函数可能由很多条指令，占了很多行，则这个函数要返回的时候，怎么回到被调用的地方呢？

---

可以用call callee来调用函数callee，然后在callee的最后一条指令用return来返回。为了记录要回到的地方，可以静态分配一片空间，用于存放这个函数的活动记录（Activation Record，AR），也即函数调用时的上下文信息。

所以call callee还会隐含ST callee.staticArea #here+20，也即将当前指令的地址存储到callee的活动记录中。return的具体实现则是和BR *callee.staticArea，也即跳转到callee的活动记录中存储的地址。

---

另一种常见的方式是栈分配。有一个栈顶指针SP（通常存放在寄存器中），call callee可以实现为：

ADD SP, SP, #caller.recordSize // 调整栈顶指针，分配空间
ST 0(SP), #here+16 // 将SP设置为SUB指令的地址
BR callee.codeArea
SUB SP, SP, #caller.recordSize // 恢复栈指针

return则实现为BR *0(SP)，也即跳转到栈顶指针所指向的地址。

4、寄存器分配

在指令的执行代价中，寄存器的代价是最小的，因此总是希望将尽可能多的运算对象放在寄存器。由于任何一个计算机模型中的寄存器个数都是有限的，因而需要根据一些原则，对寄存器进行分配。

---

一些一般原则：

• 尽可能让变量的值或中间结果保留在寄存器中，直到寄存器不够用为止。
• 进入基本块时，所有寄存器都是空闲的。到达基本块出口时，应当将有用的变量存回内存，释放所有寄存器。
• 在基本块内，后面不再被引用的变量所占用的寄存器应当尽早释放，以提高寄存器的利用效率。

5、待用信息链表法

为了做到这些，需要知道一个基本块内变量的引用情况，也即变量的待用信息。在一个基本块内，如果 A 在第 i 个四元式中被定值，在第 j 个四元式中被引用（j>i)，且 i 到 j 之间没有新的定值点，就称 j 是 i 处关于 A 的待用信息。另外，如果 A 的值在 i 之后的代码序列中被引用，则称变量在 i 处是活跃的。

---

待用信息链表法只考虑一个基本块内的待用信息。

用一个二元组表示，二元组的第一个元素表示待用信息（一个数字 i 表示在第 i 条指令备用或 F 表示非待用），第二个元素表示活跃信息（F 表示不活跃，L 表示活跃）。

建立两张表，一张是四元式-待用/活跃信息表，另一张是变量-待用/活跃信息表：

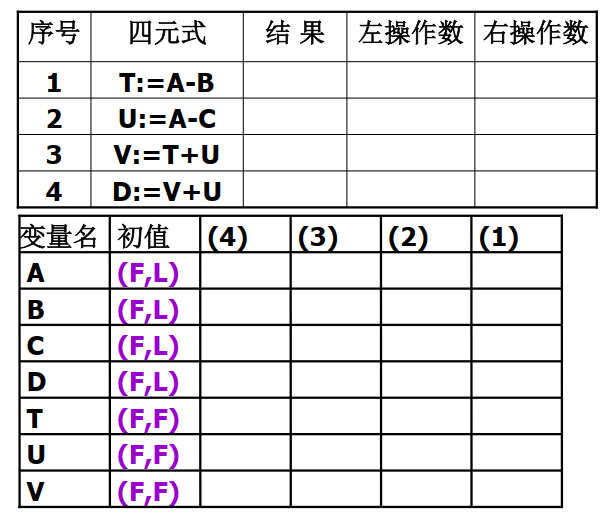
计算出各四元式各变量的待用/活跃信息的过程如下：

1. 根据已有的活跃信息，填充变量-待用/活跃信息表的初值。一开始，所有的变量都是非待用，根据时候在后续基本块被引用分为活跃和非活跃。
2. 从基本块出口开始，从后往前一次处理各个四元式。例如正在处理的四元式是i: A:=B op C：

• 将 A 当前的（也即变量-待用/活跃信息表中 A 行最右边的值）待用/活跃信息填写到四元式-待用/活跃信息表的相应位置上。
• 填写变量-待用/活跃信息表，A 在 i 处的待用/活跃信息为(F, F)，因为 i 中对 A 的定值只能在 i 以后引用，对 i 以前的四元式 A 是非活跃和非待用的。
• 将 B 当前的待用/活跃信息填写到四元式-待用/活跃信息表的相应位置上。
• 填写变量-待用/活跃信息表，对于 B 和 C，它们的在 i 处待用/活跃信息改为(i, L)，表示在 i 处是待用的，并且是活跃的。

这样，最终我们得到的四元式-待用/活跃信息表，就展示了各个四元式中各个变量的待用和活跃信息。

6、代码生成算法

用寄存器描述数组RVALUE表示寄存器的情况，RVALUE[i]={B, C}就表示变量 B 和 C 的值相同，就是寄存器 i 中存放的的值。

用变量地址描述数组AVALUE表示变量的地址，AVALUE[B]={Ri, B}就表示变量 B 的值既存放在寄存器 Ri 中，也存放在内存中（存放在内存中仍用变量名表示）。

可以定义寄存器分配函数GETREG，其以一个四元式i: A:=B op C作为输入，返回一个寄存器用于存放计算出的 A 的值。具体的规则如下：

1. 如果 B 独占寄存器 Ri，且 B 和 A 是同一个变量或 B 之后不再被引用，则R=Ri，进入第四步；否则进入第二步

2. 如果有空闲的寄存器 Ri，则R=Ri，进入第四步；否则进入第三步

3. 没有空闲寄存器，选择释放一个寄存器 Ri 作为 R。选择的寄存器对应的变量 M，最好同时也存有值在内存中，或者在基本块中引用的位置最远。然后依次做以下操作：

   • 生成目标代码ST M, Ri，将寄存器 Ri 中的值存回内存
   • 如果 M 不是 B，则令AVALUE[M]={M}，否则令AVALUE[M]={Ri, M}
   • 令RVALUE{Ri}-={M}

4. 给出 R 并返回

第九讲 代码优化

1、简介

代码优化就是对代码进行（语义）等价变换，使得变换后的代码效率更高（时间效率或者空间效率或者两者兼有）。

通常，需要在时间效率和空间效率、编译器效率和目标代码侠侣之间权衡。一般而言，更高级别的优化意味着更高效的目标代码，但是也需要花费更多时间编译，编译时的内存占用和生成代码的大小也会更高。

代码优化由三种级别——源代码优化、中间代码优化和目标代码优化。目标代码优化依赖于具体的计算机，中间代码优化不依赖于具体的计算机，我们主要讨论中间代码的优化。

根据优化涉及的范围，还可以分为：

• 局部优化（Local Optimization）：在只有一个入口和一个出口的基本块上进行优化
• 循环优化（Loop Optimization）：基于控制流分析，对循环体中的代码进行优化
• 全局优化（Global Optimization）：基于数据流分析，在整个程序范围内进行优化，关注例如变量的生命周期等

---

一些通用的技术：

• 删除公共子表达式：如果某个表达式的值在之前计算过，而且表达式中涉及到的变量值都没有变化过（表达式的值确定没变）。这种重复出现的表达式称为公共子表达式，可以删除，避免重复计算。
• 常量折叠：如果运算量都是已知的，在编译时就算出它的值。例如I:=1 T_1:=4*I可以将第二句折叠为T_1:=4，避免运行时计算。
• 常量传播：如果用一个是常量的变量赋值给另一个变量，那么可以用常量值赋值。例如接着上面的例子，还有T_4=T_1，则可以进行常量传播变为T_4=4。
• 复写传播（Copy Propagation）：如果将B的值赋给A，就称把B值复写到A。如果后面有用到A的地方，且这期间A和B的值都没有变化过，可以把对A的引用改为对B的引用，这就称之为复写传播。
• 消除死代码：
  • 变量赋值了但是从未被在程序中被引用，则赋值无用，可以删除
  • 变量赋值后没被引用，后面又重新赋值，第一次赋值无用，可以删除
  • 变量赋值仅被自己引用，则赋值无用，可以删除。将引用中的值直接替换为赋值时候的值即可。

2、局部优化

局部优化是指基本块内的优化。基本块是程序中一个顺序指向的语句序列，从第一条语句（入口语句）开始执行，进入基本块；执行完最后一条语句（出口语句）后，退出基本块。

局部优化的基本逻辑是划分基本块，然后构造基本块的 DAG，最后利用 DAG 进行优化。

---

第一步是划分基本块。

划分基本块首先要找到入口语句。以下语句是基本块的入口语句：

• 程序的第一条语句
• 转移语句的目标语句
• 紧跟在条件转移语句后的语句

上面这三种语句都意味着一个新的“执行单元”，也即基本块的开始。

找到入口语句后，为每一个入口语句构造出其所属的基本块：

• 从入口语句到下一个入口语句（不包含），构成基本块
• 从入口语句到某一转移语句（包含），构成基本块
• 从入口语句到某一停止语句（包含），构成基本块

转移语句即指有条件或者无条件跳转指令。停止语句即指程序结束等语句。出口语句一般都是终结语句，表示一个基本块的结束，例如跳转语句、返回语句、程序结束语句等。

---

第二步是构造基本块的 DAG。

构造基本块的 DAG 是一种节点带有标记或者附加信息的有向无环图。图中有两种节点：

• 叶子节点：也即没有出边的节点，代表标识符和常数。可以附加上标识符/常数的值、变量名、类型等信息
• 内部节点：也即有出边的节点，代表运算符。可以附加上运算结果、涉及的运算数等信息

具体而言，节点有三种形式：

• 0 型节点：

  

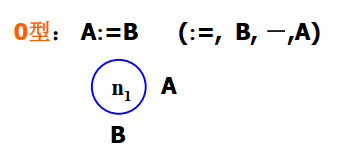
  可以表示赋值操作。这个节点旁边有A和B，表示A和B这两个变量本质相同，或者说“地址相同”

• 1 型节点：

  

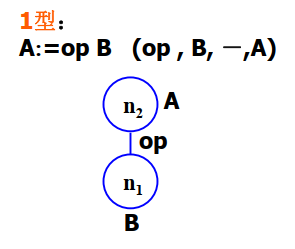
  可以表示一元运算。其中n2是操作符节点，旁边附带着A，表示运算结果。

• 2 型节点：

  

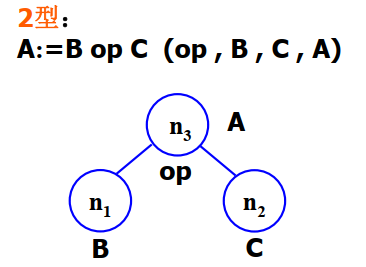
  可以表示二元运算。其中n3是操作符节点，旁边附带着A，表示运算结果。

---

第三步是利用 DAG 进行优化。

利用之前提到的公共子表达式删除、合并已知量、复写传播、删除无用赋值等方法，结合 DAG 图进行优化，删除不必要的指令即可。

3、循环优化

循环优化基于流图进行。

将控制流信息附加到基本块集合构成的有向图上构成的图，称为程序的流图（Flow Graph）。流图的节点是基本块，包含程序的第一条语句的基本块/节点是首节点；边表示控制流的转移关系。基本块$B_i$向基本块$B_j$引一条边，当且仅当：

• $B_j$在程序中的紧跟在$B_i$之后，且$B_i$的出口语句不是无条件转移语句或者停止语句
• $B_i$的出口语句是转移语句，且转移目标语句就是$B_j$的入口语句

一个例子如下：

---

接下来介绍循环优化中的优化技术：

• 代码外提：把循环不变运算移到循环外部。循环不变运算指的是结果与循环次数无关的运算，运算数是常量或者是值在循环内不会发生改变的变量。
• 强度削弱：将强度大的运算（也即复杂的运算）替换为强度小的运算，例如将乘法运算换为加法运算。
• 变换循环控制条件：将循环控制条件更换为一个等价的条件，使得变换后可以减少执行的代码条数

---

如何在流图中找到循环呢？

循环（Loop，也称自然循环）是流图中的一个子图，具有以下特征：

• 是强连通的，也即从任意一个节点出发，都可以到达其他节点
• 只有一个入口节点（首节点），首节点的唯一一条入边就是这个子图中所有节点的唯一一条入边

---

具体的确定循环的算法如下：

1. 计算支配节点集。

   从流图的首节点出发，如果到达节点$n$的任意通路都要经过$m$，就称$m$是$n$的支配节点，记为$m\ \text{DOM}\ n$。某个节点的所有支配节点的集合称为该节点的支配节点集，记为$D(n)$。

   若$n_0$为首节点，则对于任意节点$a$，一定有$a\ \text{DOM}\ a, n_0\ \text{DOM}\ a$。

2. 计算回边。

   如果存在$a\rightarrow b$的边，且$b\ \text{DOM}\ a$，则称$a\rightarrow b$是一条回边。

3. 确定循环

   如果$a\rightarrow b$是一条回边，则节点$a, b$以及不用经过$b$就能到达$a$的所有节点构成一个循环，且$b$就是循环的头节点。

   可以从$a$开始，逆着往上找，将所有不是$b$的节点都加入循环中。可以用一个栈完成这个过程：

   • 初始$a$入栈，$a, b$加入循环
   • 弹栈取得栈顶节点，找到该节点的所有父节点，如果父节点不在循环中，就入栈并加入循环；如果在循环中，什么都不做。重复上述过程，直到栈空为止

这种利用回边的算法只能找到自然循环。自然循环并不包括涵盖所有的循环，例如下图中的$\{2, 3\}$就是一个循环，但是不是自然循环：

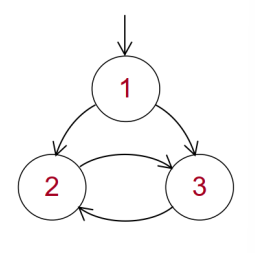
如果一个图去掉所有回边之后，就没有环了，则这个图称为可归约流图（Reducible Flow Graph）。在可归约流图中，利用回边可以找到所有的循环（都是自然循环）。结构化程序生成的流图都是可归约的。

4、全局优化

全局优化作用于整个过程（函数），可以进行跨基本块的优化，主要基于数据流分析。主要的两类数据流分析是到达——定值分析和活跃变量分析。

控制流分析中，将基本块视为一个黑盒，并不太关系基本块中的内容。而数据流分析中，将基本块视为一个白盒，需要分析基本块中的变量、赋值等等。

全局优化需要收集关于数据流的信息，包括变量如何被定义、赋值、使用等。具体而言，包括：

• 定义（Definition）：语句中对某个左值的所有赋值（变量值的所有来源）
• 使用（Use）：语句中对某个右值的所有可能引用（变量值的所有去处）
• 活跃性（Liveness）：变量在某个语句之后，是否会作为右值被使用

4.1、到达——定值分析

变量 A 的定值（Definition）是指对变量 A 的赋值语句或者读取某个值存到 A 的语句，这种语句的位置称为定值点。

变量 A 的定值点 d 能够 到达某点（某条语句）p，是指流图中，存在一条从 d 到 p 的路径，而且这条路径上没有 A 的其他定值。

作符号约定如下：

• 记$B$为基本块，$P[B]$为$B$的所有前驱基本块。
• $\text{IN}[B]$表示能够到达$B$入口处的各个变量的所有定值点的集合
• $\text{OUT}[B]$表示能够到达$B$出口处的各个变量的所有定值点的集合
• $\text{GEN}[B]$表示在$B$中，且能够到达$B$出口处的所有定值点的集合
• $\text{KILL}[B]$表示在$B$之外，且能够到达$B$的入口处，但是在$B$中被重新定值（在$B$中被杀死）的所有定值点的集合

由以上定义，显然有$\text{OUT}[B]=\text{GEN}[B]\cup (\text{IN}[B]-\text{KILL}[B])$以及$\text{IN}[B]=\bigcup_{b\in P[B]}\text{OUT}[b]$。

每个基本块的$\text{GEN}[B]$和$\text{KILL}[B]$可以直接填出，然后迭代计算$\text{IN}[B]$和$\text{OUT}[B]$，直到不再变化为止。

---

假设某点 u 引用了变量 A 的值，则把能够到达 u 的 A 的所有定值点，称为 A 在引用点u 的引用——定值链（Use-Definition Chain，UD 链）。

如果在基本块 B 中，变量 A 的引用点 u 之前有 A 的定值点 d，且 d 能够到达 u，则 A 在 u 的 UD 链就是 $\{d\}$。

如果同一个基本块内，变量 A 的引用点 u 之前没有 A 的定值点 d，则$\text{IN}[B]$ 中的 A 的定值点就是 A 在 u 的 UD 链。

4.2、活跃变量分析

对程序中某变量 A 和 A 的某定值点 p，如果存在一条从 p 开始的通路，通路中某个点引用了 p 处给 A 定的值，则称 A 在 p 处是活跃的（Active）。

作符号约定如下：

• 记$B$为基本块，$S[B]$为$B$的所有后继基本块。
• $\text{LiveUse}[B]$表示在基本块$B$中被重新定值（如果有）前有引用的变量集合（或者说在$B$中被引用之前，没有在$B$中被定值过）
• $\text{Def}[B]$表示在基本块$B$中被定值，且在定值前未在$B$中被引用过的变量集合
• $\text{LiveIn}[B]$表示在基本块$B$入口处活跃的变量集合
• $\text{LiveOut}[B]$表示在基本块$B$出口处活跃的变量集合

由以上定义，显然有$\text{LiveIn}[B]=\text{LiveUse}[B]\cup (\text{LiveOut}[B]-\text{Def}[B])$以及$\text{LiveOut}[B]=\bigcup_{b\in S[B]}\text{LiveIn}[b]$。

每个基本块的$\text{LiveUse}[B]$和$\text{Def}[B]$可以直接填出，然后迭代计算$\text{LiveIn}[B]$和$\text{LiveOut}[B]$，直到不再变化为止。

---

假设某点 u 定义了变量 A 的值，从 u 存在一条到达 A 的某个引用点 s 的路径，且这条路径上不存在 A 的其他的定值点，则所有这样的 s 的集合，就称为 A 在点 u 的定值——引用链（Definition-Use Chain，DU 链）。